 |
Задачи для самостоятельного решения
|
|
|
|
Задачи на вычисление количества информации
Для решения различных задач на определение количества информации вы должны помнить следующее:
· отношение количества вариантов (или чисел) N к количеству информации, которую несет в себе один из вариантов I: N=2I
· полный информационный объем сообщения V равен количество символов в сообщении K умноженное на количество информации на каждый символ I: V=K*I
Формула Шеннона для равновероятных событий
I=log2N
· если алфавит имеет мощность (количество символов в этом алфавите) М, то количество всех возможных «слов» (символьных цепочек) длиной N (без учета смысла) равно K=MN;
· для двоичного кодирования (мощность алфавита M –2 символа) получаем известную формулу:K=2N
Таблица степеней двойки, покажет сколько вариантов можно закодировать с помощью N бит:N
| бит | ||||||||||
| K вариантов |
1 байт = 8 бит
1 Кбайт = 210байт = 1024 байт
1 Мбайт = 210Кбайт = 1024 Кбайт
Формула Шеннона для неравновероятных событий
рi=Ki/N;
Ii=log2(1/pi);
Задание 1. Вычисление информационного объема сообщения о наступившем случайном событии. Решить задачи 1-10 (домашнее задание).
Задача №1. Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?
Задача №2. Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до100 процентов, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
|
|
|
Задача №3. Сколько существует различных последовательностей из символов «плюс» и «минус», длиной ровно в пять символов?
Задача №4. В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?
Задача №5. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в коробке?
Задача №6. В корзине лежат черные и белые шары. Среди них18 черных шаров. Сообщение о том, что достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине?
Задача №7. В некоторой стране автомобильный номер длиной 5 символов составляется из заглавных букв (всего используется 30 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным количеством байт. Определите объем памяти, необходимый для хранения 50 автомобильных номеров.
Задача №8. Для регистрации на сайте некоторой страны пользователю необходимо придумать пароль длиной ровно 11 символов. В пароле можно использовать десятичные цифры и 12 различных символов местного алфавита,причем все буквы используются в двух начертаниях – строчные и прописные. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый пароль – одинаковым и минимально возможным количеством байт. Определите объем памяти, необходимый для хранения 60 паролей.
Задача №10. Для кодирования сообщений решено использовать последовательности разной длины, состоящие из знаков «+» и «-». Сколько различных сообщений можно закодировать, используя в каждом из них не менее 2-х и не более 6 знаков?
Задание 2. Сравнение информационного объема сообщения о наступлении случайного события.
|
|
|
Пример для равновероятных событий
Какое из соотношений несет в себе БОЛЬШЕ информации:
1. x=5;
2. x>3.
Если дискретная случайная величина (д.с.в.) x равновероятно принимает целые значения.
РЕШЕНИЕ:
Согласно подходу Шенона, информации тем больше, чем меньше неопределенность. В предположении, что x - это дискретная случайная величина (д.с.в.), имеющая областью значений множество целых чисел z и равную вероятность иметь любое значение из множества z, то выражение 1) оставляет меньшую неопределенность о значении x и, следовательно, несет в себе больше информации.
Пример для неравновероятных событий
Имеется 24 шарика красного цвета, 16 шариков черного цвета. Достали красный шарик. (Отв.:?)
Пусть К1 – это количество красных шариков, К1=24
К2 – количество черных шариков, К2=8
N – общее количество шариков, N = К1 +К2=24+8=32
Вычислим вероятность выбора шарика разного цвета и количество информации, которое при этом было получено.
Вероятность выбора шарика красного цвета: р1=24/32=3/4=0,75.
Вероятность выбора шарика черного цвета: р2=8/32=1/4=0,25.
Вычислим количество информации, содержащееся в сообщении, что вытащили красный шарик: I1=log2(1/p1)= log2(1/0,75)= log21,3=1,15470 бит.
Вычислим количество информации, содержащееся в сообщении, если был выбран черный шарик: I2=log2(1/p2)= log2(1/0,25)= log24=2 бит.
1. В библиотеке 8 шкафов. Книга нашлась в 3-м шкафу; (Отв.: 1 бит)
2. Студент получил за экзамен оценку 4 (по 5-бальной системе единицы не ставят). (Отв.: 2 бита).
3. Имеется 12 шариков красного цвета, 12 шариков черного цвета. Достали красный шарик. (Отв.: 1 бит)
4. Имеется 24 шарика красного цвета, 16 шариков черного цвета. Достали красный шарик. (Отв.: 0.815 бит)
Задачи для самостоятельного решения
Задача № 1. Какое сообщение содержит большее количество информации?
1. В библиотеке 8 шкафов. Книга нашлась в 3-м шкафу; (Отв.:?)
2. Студент получил за экзамен оценку 4 (по 5-бальной системе единицы не ставят). (Отв.:?).
3. Имеется 12 шариков красного цвета, 12 шариков черного цвета. Достали красный шарик. (Отв.:?)
4. Имеется 24 шарика красного цвета, 16 шариков черного цвета. Достали красный шарик. (Отв.:?)
Задача № 2. Какое из соотношений несет в себе БОЛЬШЕ информации:
1. Х<5;
|
|
|
2. X>3.
Если д.с.в.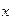 
равновероятно принимает целые значения.
Задача № 3. Какое из соотношений несет в себе БОЛЬШЕ информации:
1. X<5;
2. X>3.
Если д.с.в. 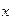равновероятно принимает натуральные значения.
Задача № 4. Какое из соотношений несет в себе БОЛЬШЕ информации:
1. X<3;
2. X>3.
Если д.с.в. 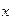принимает значения: 
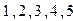, причем вероятность каждого значения пропорциональна 
.
Задание 3. Применение ЭТ для решения задач на нахождение количества информации: с использованием табличного процессора MS Excel решить задачи вычисления количества информации в сообщении о неравновероятных событиях.
|
|
|
