 |
Команды управления сопроцессора х87
|
|
|
|
ДОПОЛНИТЕЛЬНЫЕ АРИФМЕТИЧЕСКИЕ КОМАНДЫ
Введение
Дополнительные арифметические команды без явных операндов выполняют действия над содержимым вершины стека, результат помещают туда же БЕЗ МОДИФИКАЦИИ УКАЗАТЕЛЯ СТЕКА.
Ø FABS – нахождение абсолютной величины.
Ø FCHS – изменение знака операнда.
Ø FRNDINT – округление операнда до целого в формате с плавающей точкой.
Ø FSQRT – извлечение квадратного корня.
Ø FPREM – вычисляет остаток от деления содержимого ST(0) на число из ST(1). Остаток замещает число в ST(0).
Ø FSCALE – масштабирование на степень числа 2 – прибавляет целое число из ST(1) к порядку в регистре ST(0), т.е. умножает (или делит) ST(0) на число 2(ST(1)). Эту команду можно использовать для возведения числа 2 в целую степень (положительную или отрицательную).
Ø FXTRACT – разлагает содержимое ST(0) на два числа: несмещенный порядок (замещает старое значение в ST(0)) и знаковую мантиссу (включаемую сверху, т.е. в ST(7)).
Команда FSCALE, находящаяся после команды FXTRACT, восстанавливает исходное число.
Все дополнительные арифметические команды группируются в три группы:
- команды сравнений:
- трансцендентные команды;
- команды управления сопроцессора х87.
КОМАНДЫ СРАВНЕНИЙ
Команды сравнений включают:
Ø FCOM ST(i)/mem – сравнивает содержимое ST(0) с операндом "x" (в численном регистре или в памяти), т.е. производит вычитание операндов без запоминания результата и устанавливает коды условий в регистре состояния (таблица 1).
Таблица 1 – Коды условий после сравнения
| С3 | С0 | Условие |
| 0 0 1 1 | 0 1 0 1 | ST(0) > x ST(0) < x ST(0) = x ST(0) и x – не сравнимы |
Ø FICOM mem – сравнивает содержи мое вершины стека ST(0) с целым числом в памяти.
|
|
|
Ø FCOMP ST(i)/mem – аналогична команде FCOM, но после сравнения производит извлечение операнда из вершины стека.
Ø FCOMPP ST(i) – сравнивает ST(0) c ST(i) и извлекает из стека оба операнда.
Ø FTST – сравнивает вершину стека с нулем.
Ø FXAM – сравнивает вершину стека с нулем, но выставляет 4 флага условий (в частности, определяется ненормализованная мантисса, бесконечность, нечисло и др.).
Ø FCOMI ST(0),ST(i) – сравнение вещественных чисел и установка флагов в EFLAGS (P6+).
Ø FCOMIР ST(0),ST(i) – сравнение вещественных чисел и установка флагов в EFLAGS и извлечение операнда из вершины стека (P6+).
Флаги условий (С0, С3) сопроцессора х87 используются для организации условных переходов микропроцессором х86. Для этого командой – FSTSW AX – содержимое регистра состояния х87 копируется в аккумулятор АХ микропроцессора х86. После этого командой – SAHF – старший байт аккумулятора (АН) передается в младший байт регистра флагов. При этом условию С0 соответствует флаг СF, а условию С3 - флаг ZF.
ТРАНСЦЕНДЕНТНЫЕ КОМАНДЫ
К элементарным трансцендентным функциям относятся:
Ø тригонометрические функции (sin, cos, tg и др.),
Ø обратные тригонометрические функции (arcsin, arctg и др.),
Ø логарифмические функции (log2(x), log10(x), loge(x)),
Ø показательные функции (xy, 2x, 10x, ex),
Ø гиперболические функции (sh, ch, th и др.),
Ø обратные гиперболические функции (arsh, arch, arth и др.).
Таблица 2 – Трансцендентные команды
| Мнемоника | Описание команды | Вычисляемая функция |
| FPTAN | Частичный тангенс | ST(1) / ST(0) = tg (ST(0)) |
| FSIN | Синус(387+) | ST(0) = sin (ST(0)) |
| FCOS | Косинус (387+) | ST(0) = cos (ST(0)) |
| FSINCOS | Синус, косинус (387+) | ST(7) = sin (ST(0)); ST(0) = cos (ST(0)) |
| FPATAN | Частичный арктангенс | ST(0) = arctg (ST(1)/ST(0) |
| FYL2X | Двоичный логарифм | ST(0) = ST(1) * log2 (ST(0)) |
| FYL2XP1 | Двоичный логарифм | ST(0) = ST(1) * log2 (ST(0)+1) |
| F2XM1 | Показательная функция | ST(0) = 2(ST(0)) – 1 |
Сопроцессор х87 вычисляет любую из элементарных трансцендентных функций от аргументов двойной точности, давая результат двойной точности с ошибкой младшего разряда округления. Аргументы трансцендентных команд должны быть нормализованными.
|
|
|
Команда FPTAN нахождения частичного тангенса в качестве результата выдает два числа (сопроцессоры 87/287):
y / x = tg (ST(0)).
Число «y» заменяет старое содержимое ST(0), а число «x» включается сверху. Поэтому, после выполнения команды указатель стека уменьшится на 1, число «х» будет записано в новую вершину стека ST(0), а число «y» – в регистр ST(1).
Для получения значения тангенса необходимо выполнить команду FDIV. Две команды FPTAN и FDIV выбирают аргумент из вершины стека и туда же помещают значение тангенса (БЕЗ МОДИФИКАЦИИ УКАЗАТЕЛЯ ВЕРШИНЫ СТЕКА). Две команды FPTAN и FDIVR вычисляют значение котангенса.
Для команды FPTAN аргумент задается в радианах и должен находится в диапазоне (сопроцессоры 87/287):
0 <= ST(0) <= 1/4.
Для СОПРОЦЕССОРОВ 387+ аргумент команды FPTAN (в радианах) может быть любым:
–263 <= ST(0) <= +264.
Значение тангенса исходного угла tg(ST(0)) замещает аргумент и в стек включается сверху 1,0 (для программной совместимости с предыдущими сопроцессорами 87/287).
Значения остальных тригонометрических функций (для сопроцессоров 87/287) можно вычислить, используя формулы тангенса половинного угла (табл. 3). Поэтому перед началом вычисления тригонометрических функций с использованием команды FPTAN необходимо аргумент в ST(0) поделить на 2. Новое значение аргумента «z» должно также удовлетворять условию: 0 £ z £ 1/4.
Таблица 3 – Формулы для вычисления тригонометрических функций
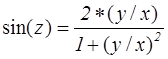
| 
|

| 
|

| 
|
команды управления сопроцессора х87
В СОПРОЦЕССОРАХ 387+ появились новые команды:
Ø FSIN – вычисление синуса;
Ø FCOS – вычисление косинуса;
Ø FSINCOS – вычисление синуса и косинуса.
Все они воспринимают в ST(0) исходный угол, измеряемый в радианах и находящийся в диапазоне: –263 <= ST(0) <= +263. Команды FSIN и FCOS возвращают результат на место аргумента, а команда FSINCOS возвращает значение синуса на место аргумента и включает значение косинуса в стек.
Команда FPATAN вычисляет arctg (ST(1)/ST(0)). Два операнда извлекаются из стека, а результат включается в стек. Поэтому окончательно, УКАЗАТЕЛЬ СТЕКА УВЕЛИЧИВАЕТСЯ НА 1. Операнды этой команды для сопроцессоров 8087/287 должны удовлетворять условию:
|
|
|
0 < ST(1) < ST(0).
В сопроцессорах 387+ ограничений на диапазон допустимых аргументов команды FPATAN не существует.
Для вычисления остальных обратных тригонометрических функций по аргументу «z» необходимо предварительно подготовить операнды в ST(0) и ST(1) в соответствии с табл. 4 (делить операнды не нужно).
Таблица 4 – Формулы для вычисления обратных тригонометрических функций

| |||||

| |||||

|

| ||||

| |||||

| |||||
Команда FYL2X вычисляет функцию: ST(1) * log2 ST(0). Два операнда извлекаются из стека, а затем результат включается в стек. Поэтому УКАЗАТЕЛЬ СТЕКА УВЕЛИЧИТСЯ НА 1. В команде требуется удовлетворение естественного для логарифмической функции условия:
ST(0) > 0.
Значения других логарифмических функций вычисляются по формулам в табл. 5 с загрузкой в регистр ST(1) необходимых констант командами: FLDLN2 и FLDLG2.
Таблица 5 - Формулы для вычисления логарифмических функций
| log2 (x) ® FLD1; FLD x; FYL2X; ln (x) = ln (2) * log2 (x) ® FLDLN2; FLD x; FYL2X; lg (x) = lg (2) * log2 (x) ® FLDLG2; FLD x; FYL2X. |
Еще одна логарифмическая команда FYL2XP1 вычисляет функцию: ST(1) * log2 (ST(0) + 1). Причина появления этой команды заключается в получении более высокой точности вычисления функции: log(1 + x). Эта функция часто встречается в финансовых расчетах, а также при вычислении обратных гиперболических функций.
Команда показательной функции F2XM1 вычисляет:
F2XM1 [ST(0)] = 2(ST(0)) – 1.
Аргумент показательной функции должен находится в диапазоне: для сопроцессоров 87/287: 0 <= ST(0) <= 0.5;
для сопроцессоров 387+: –1 <= ST(0) <= +1.
Вычисление функции 2х – 1 вместо функции 2х позволяет избежать потери точности, когда аргумент «х» близок к 0 (а значение функции 2х близко к 1). Остальные показательные функции вычисляются по формулам в табл. 6.
Таблица 6 – Формулы для вычисления показательных функций
| 2x = [2x – 1] + 1 = F2XM1 (x) + 1; ex = 1 + [2(x * log2(e)) – 1] = 1 + F2XM1 (x * log2(e)); 10x = 1 + [2(x * log2(10))– 1] = 1 + F2XM1 (x * log2(10)); аx = 1 + [2(x * log2(а)) – 1] = 1 + F2XM1 (x * log2(a)). |
|
|
|
Таблица 7 – Формулы для вычисления гиперболических функций
| Cинус гиперболический | 
|
| Косинус гиперболический | 
|
| Тангенс гиперболический | 
|
| Котангенс гиперболический | 
|
| Косеканс гиперболический | 
|
| Секанс гиперболический | 
|
Таблица 8 – Формулы для вычисления обратных гиперболических функций
 где:
где: 
|
 где:
где: 
|
 где:
где: 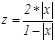
|

|

|

|
|
|
|


