Реальные газы. Уравнение Ван – дер - Вальса .

Вязкость. Коэффициент вязкости.

Явл. вязкости в газе - это направленный перенос импульса упорядоченного движения молекул за счет их хаотичного движ при наличии градиента скорости упорядочн движ

Импульс упорядочен. движ равен переносимый через ∆S:

По 2 закону Ньютона: изменение импульса слоя = импульсу силы трения, действ за в направлении скор параллельной

т.е. Fтр =

fтр = =

Закон Внутр трения(вязкости) Ньютона:

fтр= - ; η – к-т динамической вяз-ти

Сила внутр тр при макроскопич движении газа пропорциональна градиенту скор газа упорядочн движ. Возникает за счёт переноса импульса. Коэффициент вязкости численно равен силе внутр тр, на ед S при градиенте скор = -1,

Киниматич коэф вязкости есть динамич дел на

, [м² /с]

Не Ньтоновская вязкость жидкости:

 

Фазовые равновесия и превращения. Фазы и фазовые превращения.

Фазой наз. Макроскопическое физически однородная часть вещества, отделенная границами от остальн части сист. В сист может быть несколько ТВ и жидк фаз, но газообразн только 1. Различн фазы явл агрегатн сост вещва (ж, т, г). Фаза - более широкое понятие, чем агрегатное сост вещва могут сущ различн фазы одного агр сост. Различн фазы одного и того же вещва могутнаходиться в тепловом и механич равновесии. При тепловом равновесии темпер фаз одинакова, при механич равновес существование 2 фаз возможно при опр знач t и p. Переход вещва из 1 фазы в 2 – это фазовый переход. Различают фазовый переход 1 и 2 –го рода. Примеры: сублимация, испарение, кристаллизация, плавление.

Равновесие 2 фаз возможно только вдоль определённой линии: p = p(t). Равновесие 3 фаз – в одной точке (тройной):

t_тр = 0,01^оС

p_ТР = 4,62 мм рт ст

возможно существование нескольких тройных точек.

Фазовый переход 2-го рода не связаны с теплотой фаз перехода, они связаны с модификацией кристалл решетки при этом могут меняться скачком такие характеристики: теплоемкость, коэф тепл расшир

Фазовый переход 2-го рода, пример:

1) Переход некоторметаловпри сверхнизких темпер в сверх проводящ расстояния

2) Переход ферромагнетика железа в обычн паростаметик со слабым магн свовами.

3) Переход Гелий 1 в Гелий 2 (где энта=0)

Уравнение Клайперона - Клаузиса.

Получим зависимость давления от темпер при котор возможно равновесие 2 фаз вещва

Переход из фаз1 в фазу 2 происходит изотермически при темпер t. Адиабатический процесс СВ.

Цикл Карно.

Переход из 1 в 2 вдоль изотермы

T + dT.

Работа такого цикла:

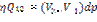
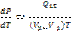-Урние Клайперона-Клаузиса

Показ как меняется давление и темпер.

Пусть объём и тепло отнесены к 1 моль в-ва, тогда говор об удельных вел-ах. При переходе воды в пар V > (V₂ > V₁), T > 0, dp/dt > 0

Процесс возможен если он имеет след зависимость:

 

 

Реальные газы. Уравнение Ван – дер - Вальса.

При больших давлениях (р>200атм) и низких темп (Т<50К) наблюд знач отклон в поведении реальн газа от состояния идеальн газа опис-ми ур Клайп - Менделева. Это отношение обусл 2 причинами:

1) Нельзя пренебрегать собств размерами молекул. Расчет показ, что при давл 5 тыс атм на собств оббьем мол-кул приходиться половина всего обьема газа.

2) Мол-лы взаимодеств. Между собой силами притяж и отталкив

Потенциальн энергия взаимодеств мол в зависим от раст – энерг описыв потенциалом Леннарда – Джонса:

С₁ и С₂ – полож компоненты, знач на близк раст. На близких расстояниях силы отталкивания мощные dA=Fdr =- F= -

Из больш чилса урний сост (>100) описыв поведение реальных газов наиболее удачным оказыв урние ВдВ для 1 моль:

(P+ Урние ВДВ

a и b постоянные ВДВ. Различные для разн газов

Покажем, что поправка в – есть 4-ный собственный объём всех молекул 1 моль газа.

Для движ сталкив мол-л оказ недоступный объём (шара – пунктир).

V = 4/3*πd³

V₁ =4/3*π(d/2)³=4/3*πd³*1/8

V = 8 V₁

Недоступн для движ оказ 8-ный объём мол-лы (на 2 мол-лы). Для 1 моль у 4-ный (V=4V₁)

Поскольку число мол N_A/V_O, то недост для движ оказ объём: в = N_A4V₁. тогда (V_O – в) – объём доступн для движ мол-лы газа. покажем, что 2-ая попр а связ с учётом сил сцепления, притяж мол-л между собой. В силу сил притяж м-л удары мол-л о стенки сосуда несколько смягчены и газ заним меньш объём, чем по зак Боуля – Мариотта, как если бы он наход под несколько больш давлен.

Мол-ное давлен прямопропорц как числу м-л в 1-ом слое, так и числу м-л во 2-ом слое, те пропорц произвед числа м-л в слое 1 и 2:

р ~ N·N, p ~ n·n ~ N_А/ V_O * N_А/ V_O

р = 1/ V_O → р* = а / V_O – мол-ное избыт давл.

ВдВ для числа молей ν, V = ν V_O, V_O = V/ ν

(р + (а ν²)/ V²)(V - в ν) = νRT

Из ВдВ как частн случ выт ур Менд–Клайп:

р V(1 +(а ν²)/ рV·V)(1 – (в ν)/ V) = νRT

V→∞, р V = const, р V = νRT – ур М-Кл.

 

1^о. Кинематика поступательного движения.

2^о. Кинематика вращательного движения.

3^о. Динамика частиц. Закон ньютона.

4^о. Неинерциальные системы отсчета (НСО). Силы инерции.

5^о. Основное ур-ние динамики вращательного движения тв. тела.

6^о. Момент инерции тела. Теорема Штейнера.

7^о. Закон сохранения импульса.

8^о. Работа. Мощность. Кинетическая энергия системы.

9^о. Потенциальная энергия системы.

Поделиться:

Воспользуйтесь поиском по сайту: