 |
Применение итерационных методов
|
|
|
|
Оглавление
Введение 3
§1. Уточнение решения 4
§2. Метод простых итераций 7
§3. Метод Гаусса – Зейделя 14
§4. Применение итерационных методов 16
Список использованной литературы 19
Введение
Все используемые на практике методы решения систем линейных алгебраических уравнений можно разделить на две большие группы: точные методы и итерационные методы.
Под точным методом решения понимается метод, позволяющий теоретически получить точное значение всех неизвестных в результате конечного числа арифметических операций. (метод Крамера)
Итерационные методы позволяют получить решение лишь в виде предела последовательности векторов, построение которого производится единообразным процессом, называется процессом итерации, или последовательных приближений.
Вдобавок, итерационные методы находят широкое применение и при решении еще одной вычислительной задачи линейной алгебры, называемой полной проблемой собственных значений (отыскание всех собственных значений и отвечающих им собственных векторов заданной матрицы), т.к. намного удобнее вычислить предел некоторых числовых последовательностей без предварительного определения коэффициентов характеристического многочлена.
Преимуществом итерационных методов является удобное применение в современной вычислительной технике, т.к. решения, полученные с помощью прямых методов обычно содержат погрешность. Итерационные методы же позволяют получить решение данной системы с заранее определенной погрешностью. Явным преимуществом является значительное превосходство над точные методы по скорости и удобнее реализуются на практике.
|
|
|
Уточнение решения
Полученные с помощью прямых численных методов решения обычно содержат погрешность, вызванную округлениями при выполнении операций над числами с плавающей точкой. В некоторых случаях эти погрешности могут оказаться недопустимо большими. Рассмотрим один из методов уменьшения погрешности численного решения СЛАУ.
Найдем решение системы линейных уравнений
 (1.1)
(1.1)
Пусть с помощью некоторого метода получено приближенное решение  (начальное приближение к решению). Подставив в (1.1), получим
(начальное приближение к решению). Подставив в (1.1), получим
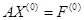 (1.2)
(1.2)
Обозначим за  погрешность полученного решения,
погрешность полученного решения, 
 - невязка.
- невязка.
Вычитаем (1.2) из (1.1), с учетом введенных обозначений
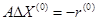 (1.3)
(1.3)
Решив эту систему получим новое значение погрешности  , которое используем в качестве поправки к приближенному решению
, которое используем в качестве поправки к приближенному решению  , получая таким способом новое приближение
, получая таким способом новое приближение  (следующее приближение к решению):
(следующее приближение к решению):
 .
.
Таким же способом найдем следующее приближение  и следующую поправку к приближению
и следующую поправку к приближению  . Подобным образом будем искать очередные значения погрешности и поправки, пока погрешность
. Подобным образом будем искать очередные значения погрешности и поправки, пока погрешность 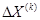 не станет достаточно малым. Таким образом мы найдем приближенное решение системы с заданной точностью.
не станет достаточно малым. Таким образом мы найдем приближенное решение системы с заданной точностью.
Рассмотренный выше процесс фактически является итерационным методом решения системы линейных уравнений, при этом следует отметить небольшой объем вычислений, т.к. на каждой итерации решаются системы уравнений вида (1.3) с одной и той же матрицей, т.е. нет необходимости преобразовывать матрицу. Такой подход позволяет строить экономичные с точки зрения машинного времени алгоритмов.
|
|
|
Следует заметить, что если при увеличении числа итераций приближенное решение стремится к точному:
 ,
,
то итерационный метод называют сходящимся.
Наличие сходимости и достижения заданной точности на практике можно определить (приближенно) несколькими способами. Так, при заданной погрешности 
 (1.4),
(1.4),
 , (1.5),
, (1.5),
 , при
, при 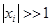 (1.6).
(1.6).
Здесь в (1.4) отличие векторов 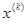 и
и  на «ε» понимается как малость модуля их разности. В (1.5) – малость разностей всех компонентов вектора, в (1.6) в смысле малости относительных разностей компонент. В случае, когда система не является плохо обусловленной, то в качестве критерия достижения нужной точности можно принять условие малости невязки:
на «ε» понимается как малость модуля их разности. В (1.5) – малость разностей всех компонентов вектора, в (1.6) в смысле малости относительных разностей компонент. В случае, когда система не является плохо обусловленной, то в качестве критерия достижения нужной точности можно принять условие малости невязки:
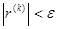 . (1.7)
. (1.7)
§2. Метод простых итераций (метод Якоби)
Рассмотрим квадратную систему линейных уравнений с вещественными коэффициентами, которую запишем в матричном виде (1.1).
 .
.
Предполагая однозначную разрешимость системы (1.1), заменим матричное уравнение эквивалентным ему уравнением:
 , (2.1)
, (2.1)
где τ – вещественное число, называемое стационарным параметром. С помощью (2.1) составим итерационную последовательность векторов  , определив её рекуррентно:
, определив её рекуррентно:
 (k = 0,1,2,…..) (2.2)
(k = 0,1,2,…..) (2.2)
при произвольном выборе нулевого приближения.
Таким образом, метод простой итерации сводится к замене точного решения системы (1.1) k – ой итерацией  с достаточно большим номером k.
с достаточно большим номером k.
Графически метод Якоби можно представить следующим образом:

Рис. 1. Схема выполнения метода Якоби
Оценим погрешность  метода простой итерации. Очевидно, что
метода простой итерации. Очевидно, что
 , (2.3)
, (2.3)
где Е – единичная матрица.
Введем в рассмотрение норму вектора в пространстве 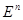 и операторную норму квадратной матрицы порядка
и операторную норму квадратной матрицы порядка  . Назовем нормой вектора
. Назовем нормой вектора  число
число  , равное длине вектора. Назовем операторной нормой произвольной матрицы
, равное длине вектора. Назовем операторной нормой произвольной матрицы  число
число  , равное либо точной верхней грани отношения
, равное либо точной верхней грани отношения  на множестве всех ненулевых векторов
на множестве всех ненулевых векторов  , либо (что одно и то же) точной верхней грани норм
, либо (что одно и то же) точной верхней грани норм  на множестве всех векторов
на множестве всех векторов  , имеющих единичную норму. Т.е по определению
, имеющих единичную норму. Т.е по определению
 . (2.4)
. (2.4)
Из (2.4) вытекает неравенство, справедливое для любой матрицы  и любого вектора
и любого вектора  :
:
|
|
|
 . (2.5)
. (2.5)
Из матричного уравнения погрешности (2.3) и неравенства (2.5) получаем, что для любого номера  :
:
 . (2.6)
. (2.6)
Теорема 2.1. Для того, чтобы итерационная последовательность (2.2) при любом выборе начального приближения 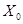 и при данном значении параметра
и при данном значении параметра  сходилась к точному решению
сходилась к точному решению  системы (1.2), достаточно, чтобы было выполнено условие
системы (1.2), достаточно, чтобы было выполнено условие
 . (2.7)
. (2.7)
При этом итерационная последовательность сходится со скоростью геометрической последовательности со знаменателем  .
.
В случае если матрица  является симметричной, условие является необходимым условием сходимости итерационной последовательности при любом выборе нулевого приближения.
является симметричной, условие является необходимым условием сходимости итерационной последовательности при любом выборе нулевого приближения.
Для практических же целей недостаточно установить факт сходимости последовательности итераций. Центральным вопросом является оценка скорости сходимости. Очень важно знать, как наилучшим способом распорядиться стационарным параметром  для того, чтобы получить наиболее быструю сходимость.
для того, чтобы получить наиболее быструю сходимость.
Пусть задана точность  - точность, с которой необходимо получить решение системы. Требуется найти итерацию
- точность, с которой необходимо получить решение системы. Требуется найти итерацию  с таким номером
с таким номером 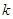 , для которого
, для которого
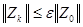 . (2.8)
. (2.8)
Из (2.6) и Теоремы 2.1 следует, что 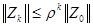 , и (2.8) выполняется при условии
, и (2.8) выполняется при условии  , т.е при
, т.е при  . Отсюда видно, что для уменьшения числа итераций
. Отсюда видно, что для уменьшения числа итераций  , достаточных для достижения заданной
, достаточных для достижения заданной  - точности, следует выбрать параметр
- точности, следует выбрать параметр  так, чтобы получить минимум функции
так, чтобы получить минимум функции  .
.
Считая матрицу  симметричной и положительно определенной, мы приходим к следующей задачей оптимизации: найти минимум функции
симметричной и положительно определенной, мы приходим к следующей задачей оптимизации: найти минимум функции
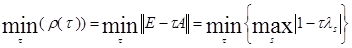 .
.
Теорема 2.2 (Теорема А.А. Самарского). Пусть матрица  является симметричной и положительно определенной, а матрица
является симметричной и положительно определенной, а матрица  положительно определенной. Тогда для того, чтобы итерационная последовательность
положительно определенной. Тогда для того, чтобы итерационная последовательность
 (2.9)
(2.9)
при любом выборе нулевого приближения 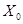 сходилась к точному решению
сходилась к точному решению  системы
системы 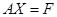 , достаточно, чтобы были выполнены условия
, достаточно, чтобы были выполнены условия
 (2.10)
(2.10)
При дополнительно предположении о том, что матица является симметричной, условие (2.10) не только достаточно, но и необходимо для сходимости указанной итерационной последовательности с любым нулевым приближением 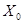 .
.
|
|
|
Выражение (2.9), где  представляет себя некоторую «легко обратимую» квадратную матрицу
представляет себя некоторую «легко обратимую» квадратную матрицу  - го порядка, а
- го порядка, а  - стационарный параметр, получается из выражения (2.2). Такой метод является более общим методом по сравнению с методом простой итерации и называется «неявным методом простой итерации».
- стационарный параметр, получается из выражения (2.2). Такой метод является более общим методом по сравнению с методом простой итерации и называется «неявным методом простой итерации».
Перейдем теперь к оценке сходимости общего неявного метода простой итерации. Для этого выясним вопрос о выборе стационарного параметра  , обеспечивающего наиболее быструю сходимость последовательности.
, обеспечивающего наиболее быструю сходимость последовательности.
Предположим, что  является симметричной и положительно определенной. С помощью таких матриц естественно ввести так называемое «энергетическое скалярное произведение» двух произвольных векторов
является симметричной и положительно определенной. С помощью таких матриц естественно ввести так называемое «энергетическое скалярное произведение» двух произвольных векторов  и
и  , положив его равным
, положив его равным  Такое скалярное произведение будем обозначать
Такое скалярное произведение будем обозначать 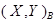 . С помощью матрицы
. С помощью матрицы  это скалярное произведение можно записать в виде
это скалярное произведение можно записать в виде  С помощью последнего равенства легко проверяется справедливость для введенного нами скалярного произведения четырех аксиом скалярного произведения.
С помощью последнего равенства легко проверяется справедливость для введенного нами скалярного произведения четырех аксиом скалярного произведения.
Далее естественно ввести «энергетическую норму» вектора  , положив ее равной
, положив ее равной  . Эту энергетическую норму обозначим как
. Эту энергетическую норму обозначим как  .
.
Две различных нормы одной и той же системы векторов 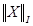 и
и 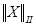 называются эквивалентными, если существуют такие положительные постоянные
называются эквивалентными, если существуют такие положительные постоянные 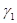 и
и  , что справедливы неравенства
, что справедливы неравенства
 . (2.11)
. (2.11)
Энергетическая и обычная нормы вектора являются эквивалентными, а это позволяет утверждать, что последовательность  сходится к нулю тогда и только тогда, когда сходится к нулю последовательность
сходится к нулю тогда и только тогда, когда сходится к нулю последовательность  . Для дальнейших же рассуждений энергетическая форма более удобна.
. Для дальнейших же рассуждений энергетическая форма более удобна.
Теорема 2.3 Пусть матрица  и
и  симметричны и положительно определены,
симметричны и положительно определены,  - погрешность общего неявного метода простой итерации. Тогда для того, чтобы при
- погрешность общего неявного метода простой итерации. Тогда для того, чтобы при 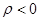 было справедливо неравенство
было справедливо неравенство 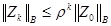 , необходимо и достаточно, чтобы было выполнено следующее условие
, необходимо и достаточно, чтобы было выполнено следующее условие
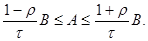 (2.12)
(2.12)
Применим Теорему 2.3 для нахождения значения стационарного параметра  , при котором скорость сходимости будет максимальной. Как уже было сказано выше, для этого необходимо найти минимум функции
, при котором скорость сходимости будет максимальной. Как уже было сказано выше, для этого необходимо найти минимум функции
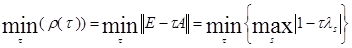
Так как обе матрицы  и
и  являются симметричными и положительно определенными, то существуют такие постоянные
являются симметричными и положительно определенными, то существуют такие постоянные  и
и  , что справедливы неравенства
, что справедливы неравенства  . Будем считать, что постоянные
. Будем считать, что постоянные  и
и  в этих неравенствах нам заданы. Сопоставляя это неравенство с условием (2.12), мы получим, что минимальное значение
в этих неравенствах нам заданы. Сопоставляя это неравенство с условием (2.12), мы получим, что минимальное значение  достигается при условии
достигается при условии  , откуда получаем, что оптимальное значение параметра
, откуда получаем, что оптимальное значение параметра  и минимальное значение
и минимальное значение 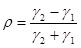 .
.
|
|
|
Частным случаем приведенного рассмотрения является явный метод простой итерации, для которого справедливы все полученные выше результаты.
Метод Гаусса-Зейделя
Рассмотрим еще один итерационный метод решения систем линейных алгебраических уравнений. Метод Гаусса-Зейделя заключается в последовательном выражении неизвестных. Этот метод является одним из самых распространенных и наиболее легко программируемых.
Пусть задана СЛАУ
 (3.1)
(3.1)
Предположим, что диагональные элементы не нулевые (в противном случае можно переставить уравнения). Выразим неизвестные из каждого уравнения:
 (3.2)
(3.2)
Зададим некоторые начальные (нулевые) приближения значений неизвестных:  , подставляя эти приближения в первое уравнение системы (3.2), получим новое (первое) приближение для
, подставляя эти приближения в первое уравнение системы (3.2), получим новое (первое) приближение для  . Используя это значение и нулевые приближения для других неизвестных получим новое приближение для
. Используя это значение и нулевые приближения для других неизвестных получим новое приближение для 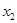 и т.д. до
и т.д. до  .
.
На этом заканчивается первая итерация решения системы. Используя теперь полученные приближения таким же образом проводи вторую итерацию.
Итерационный процесс продолжается до тех пор, пока значения неизвестных не станут отличаться от предыдущих приближений на 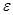 .
.
Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов (преобладание диагональных коэффициентов):

При этом хотя бы для одного уравнения это неравенство должно выполняться строго. Эти условия являются достаточными для сходимости метода, но не являются необходимыми, т.е. для некоторых систем метод сходится и при нарушении условий.
Графически метод Зейделя можно представить следующим образом:
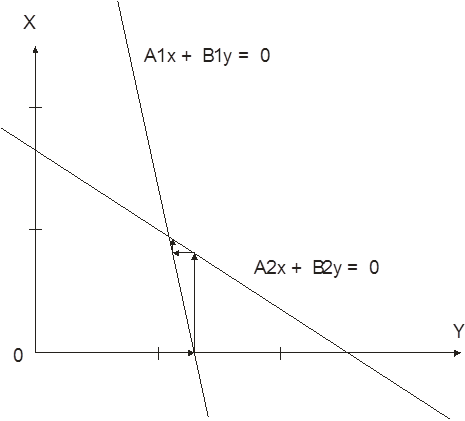
Рис. 2. Схема выполнения метода Гаусса-Зейделя
Применение итерационных методов
Покажем применение итерационных методов на конкретном примере. Для этого, решим систему уравнений вида
 (1.1)
(1.1)
Возьмем для удобства матрицу  двухдиагональной, и размерностью
двухдиагональной, и размерностью  , и произвольный вектор
, и произвольный вектор  , т.е. матрицы вида
, т.е. матрицы вида
 ,
, 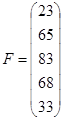 (4.1)
(4.1)
Так как можно доказать, что все собственные числа  матрицы по модулю меньше единицы:
матрицы по модулю меньше единицы:
 (4.2)
(4.2)
То для решения системы (1.1) с заданными коэффициентами (4.1) можно применить как итерационный метод Якоби, так и метод Гаусса-Зейделя.
Точным решением системы является вектор  .
.
После применения итерационные методы Якоби и Гаусса-Зейделя были получены следующие результаты:
| Метод решения | 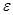 (погрешность) (погрешность)
|  (стацион. параметр) (стацион. параметр)
| Полученное решение | Время решения |
| Якоби | 0.000001 | 1 | 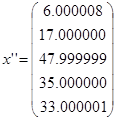
| 16 мс. |
| Якоби | 0.000001 | 
| 09 мс. | |
| Зейделя | 0.000001 | 1 | 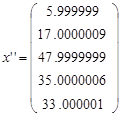
| 09 мс. |
| Зейделя | 0.000001 | 
| 05 мс. |
Табл. 1. Полученные результаты
Из таблицы видно, что при одинаковой требуемой погрешности используя разные итерационные методы были получены различные результаты.
Легко заметить, что при произвольном выборе стационарного параметра  метод Зейделя значительно превосходит метод Якоби по скорости. И, хотя разница во времени относительно небольшая, следует учесть сравнительно небольшую размерность системы уравнений. Естественно, при увеличении размерности скорость сходимости методов неоднократно возрастет.
метод Зейделя значительно превосходит метод Якоби по скорости. И, хотя разница во времени относительно небольшая, следует учесть сравнительно небольшую размерность системы уравнений. Естественно, при увеличении размерности скорость сходимости методов неоднократно возрастет.
Так же следует отметить сильное различие в скорости сходимости при произвольном стационарном параметре и при специальном (оптимизированным) выборе 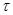 .
.
Из полученных результатов можно сделать вывод, что для решения систем линейных уравнений, для которых выполняется условие (4.1) наиболее оптимальным (по скорости сходимости) является метод Гаусса-Зейделя с оптимизированным набором параметров. Но для достаточно небольших систем линейных уравнений может использоваться метод Якоби с оптимизированным набором параметров.
Таким образом, можно сделать вывод, что итерационные методы хорошо подходят для уточнения решения, полученного с помощью любого точного (прямого) метода. Итерационные методы могут применяться и для систем, но только для удовлетворяющих некоторым условиям (как условие (4.1) метода Якоби).
Оптимальным же является комплексное применение методов решения СЛАУ, т.е. получение приближенного решения с помощью прямого метода и последующего уточнения решения с помощью итерационных методов.
Список использованной литературы
1. Турчак Л.И., Плотников П.В. Основы численных методов: Учебное пособие. – 2-е изд., перераб. и доп. – М.:ФИЗМАТЛИТ, 2003. – 304с.
2. Бояршинов М.Г. Численные методы. часть1: Учебное пособие для студентов направления «Прикладная математика и информатика». – Перм. Гос. Техн. Ун-т. Пермь, 1998. – 176с.
3. Ильин В.А., Позняк Э.Г. Линейная алгебра: Учеб.: Для Вузов. – 5-3 изд. – М.:ФИЗМАТЛИТ, 2002. – 320с.
4. Самарский А.А., Гулин А.В. Численные методы: Учеб. Пособие для вузов. – М.:Наука. Гл.ред физ.-мат. Лит-ры, 1989. – 432с.
5. Калиткин Н.Н. Численные методы. – М.:Наука. Гл.ред. физ.-мат. Лит-ры, 1978. – 512с.
|
|
|


