Дисконтирование и учет по простым процентным ставкам

Слово «процент» имеет два наиболее употребительных значения. Первое – математическое – означает сотую долю какого-либо количества. В абстрактном случае – просто сотую долю числа. Второе – «экономическое» - выражает плату за использование средств (ссуда, кредит), предоставляемых одним лицом (кредитором) другому лицу (заемщику, дебитору). Величина суммы оплаты определяется обычно как процент (в математическом смысле) от суммы долга. В основе таких сделок лежат заранее оговоренные их субъектами правила получения дохода на процент от предоставления денег в долг. Таким образом, процент выступает как причина изменения стоимости денег во времени. Однако нужно помнить, что в финансовых расчетах процент рассматривается не только как плата за пользование заемными средствами, а шире – как показатель доходности любого вложения капитала.

Процентными деньгами, или процентами называют сумму, которую уплачивают за пользование денежными средствами. Это абсолютная величина дохода. Отношение процентных денег, полученных за единицу времени, к величине капитала называется процентной ставкой.

Методы финансово-экономических расчетов различны в зависимости от вида применяемых процентов. Относительно момента выплаты или начисления дохода за пользование предоставленными денежными средствами проценты подразделяются на обычные и авансовые. Обычные (декурсивные) проценты начисляются в конце периода относительно исходной величины средств. Доход на процент выплачивается в конце периодов финансовой операции.

Если же доход, определяемый процентом, выплачивается в момент предоставления кредита, то данная форма расчетов называется авансовой или учетом, а применяемые проценты – авансовыми (антисипативными), которые начисляются в начале периода относительно конечной суммы денег.

Период начисления процентов – отрезок времени между двумя следующими друг за другом процедурами взимания процентов или срок финансовой операции, если проценты начисляются 1 раз в год.

Практика уплаты процентов основывается на теории наращивания денежных средств по арифметической или геометрической прогрессии.

Арифметическая прогрессия соответствует простым процентам, геометрическая – сложным, т.е. в зависимости оттого, что является базой для начисления – переменная или постоянная величина.

Проценты делятся на:

- простые, которые весь срок обязательства начисляются на первоначальную сумму;

- сложные, база для начисления, которых постоянно меняется за счет присоединения ранее исчисленных процентов.

Термин дисконтирование употребляется как средство определения

любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени.

В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например при разработке условий контракта. Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этом случае говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называется учетом, а удержанные проценты - дисконтом. В зависимости от вида процентной ставки применяют два метода дисконтирования - математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором - учетная ставка.

Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды.

,

,

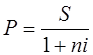где D - дисконта.

Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. При учете векселя применяется банковский или коммерческий учет, согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d.

,

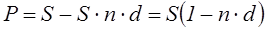Для ставки наращения прямой задачей является определение наращенной суммы, обратной - дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная - в наращении.

Ставка Прямая задача Обратная задача

i  

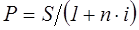
d  

Учетная ставка отражает фактор времени более жестко. Например, при d = 20 % уже 5-ти летний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете.