 |
Расчет сжатого стержня на устойчивость.
|
|
|
|
По курсу: «Сопротивление строительных материалов (часть 2)»
Выполнил: студент группы:
ПГСб-15ZD1 Зырянова Е. Н.
Шифр/№ студ.билета: ПГСб-15-22
Проверил: Матвеев С. А.
Омск – 2017
Номер варианта:
Мой шифр ПГСб-15-22. Номер схемы - 2, номер варианта (номер строки) - 2.
Расчет жесткого бруса на внецентренное сжатие
1. Определить положение центра тяжести сечения.
2. Определить положение нулевой линии относительно центральных осей
3. Определить значение сжимающей силы.
4. Определить напряжения в характерных точках сечения.
5. Построить эпюру напряжений.
6. Построить ядро сечения.
а = 0,3 м;
Rсж = 10 Мпа;
Rp = 3 МПа.
Решение:
1. Определение положениz центра тяжести сечения.
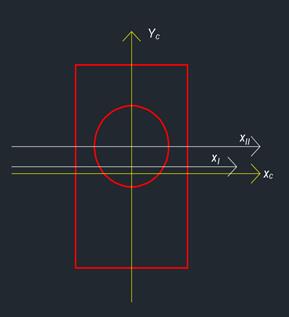
Разбиваем сечение на две фигуры: прямоугольник (I) и круг (II). В центре тяжести каждой из фигур проводим местные центральные оси. В произвольных осях X и Y определим положение центра тяжести всего сечения.
Xс= 0, так как ось Yc является осью симметрии.
Yc= Sx/ A = (S Ix- S IIx) / (AI-AII)
Через точку Спроводим главные центральные оси Yc, Xc.
2. Определение положения нулевой линии
Определяем главные центральные моменты инерции относительно осей Yc, Xc.
Ixc= IIxc- IIIxc= IIx1+ AI*a21- IIIx2+AII*a22;
Iyc= IIyc- IIIyc = IIy1+ AI*a21- IIIy2+ AII*a22;
Определяем квадраты радиусов инерции сечения:
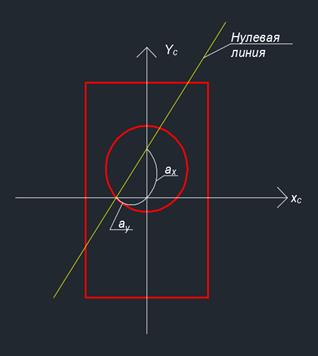
Находим отрезки, отсекаемые нулевой линией по осям координат, вычислив, что x2= 0,45 м; y2= -0,7 м:
Строим нулевую линию.
3.Определение значение сжимающей силы.
Наиболее удалены от нейтральной линии следующие точки:
- точка 1, координаты которой x1= - 0,45, и y1 = 0,7;
- точка 7, координаты которой x2 = 0,45, и y2 = - 0,77.
Для этих точек должны соблюдаться условия прочности – действующие в них напряжения не должны превышать расчетных сопротивлений материала:
|
|
|
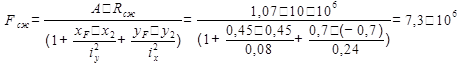
Из двух значений F выбираем наименьшее: Fдоп = 7,3*106 Н.
4. Построение ядра сечения
Для заданного сечения проводим несколько нулевых линий I-I, II-II, III-III, IV, касающихся контура сечения. Определим отрезки ах и аy, отсекаемые нулевыми линиями по координатным осям.
Для положений нулевой линии I-I: ax=∞; ay =0,8.
Координаты ядра сечения:
Для положений нулевой линии II-II: ax=0,45; ay =∞.
Координаты ядра сечения:
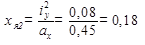
Для положений нулевой линии III-III: ax=∞; ay = - 0,7.
Координаты ядра сечения:
Для положений нулевой линии IV - IV: ax=- 0,45; ay = ∞.
Координаты ядра сечения:
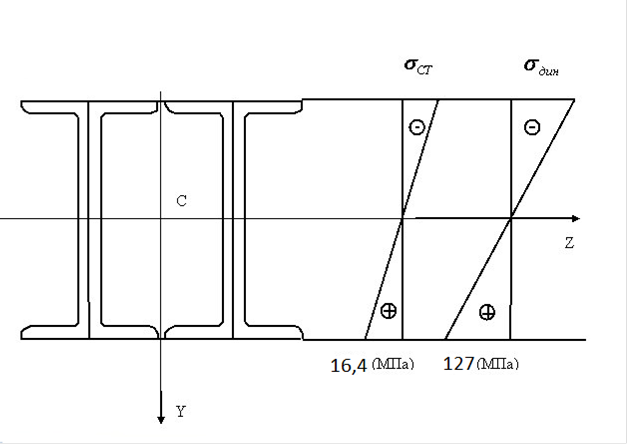
5. Определение напряжения в характерных точках сечения и п остроение эпюры σ.
Используя общую формулу:
вычисляем нормальные напряжения в характерных точках сечения:
 |
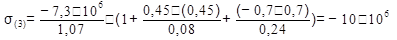
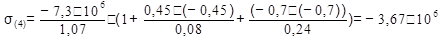
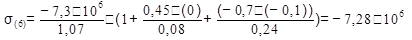
Расчет бруса на динамическое действие нагрузки
Построить эпюру изгибающих моментов от статического действия груза U.
2. Определить размеры поперечного сечения (двутавр)
3. Определить статический прогиб в точке падения груза Q.
4. Определить динамический коэффициент.
5. Определить величину изгибающего момента и максимального нормального напряжения при ударе.
Q = 0,8 кН,
h = 0,09 м,
L = 5,4 м,
Ru = 190 МПа.
Решение:
1. Определение реакции опор:
;
;
;
.
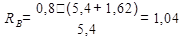2. Определяем изгибающий момент
при статическом приложении груза Q.
=1.3 кН.
Строим эпюру Мст.
.
3. Определение прогиба в сечении С при статическом приложении Q. Применим метод начальных параметров для определения VC. Для сечения «х» уравнение прогиба по методу начальных параметров:
,
Где V0 – начальный прогиб;
– начальный угол поворота;
Q0 = RA – поперечный сила при х = 0.
Для определения используем условие: V(x)I(x=l)= 0
;
;
.
Учетом найденного значения запишем выражение для прогибов:
.
Найдем прогиб в сечении С при х=0.3*l:
;
.
4. Определение размеров поперечного сечения из условия прочности при сгибе:
|
|
|
;
;
.
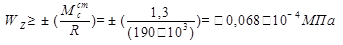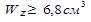Для двутавра № 10:
;
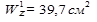Из сортамента определяем:
;
5. Определяем коэффициент динамичности:
;
.
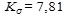6. Определение изгибающего момента при ударе:
.
7. Определение напряжения при ударе:
.
Стром эпюру.
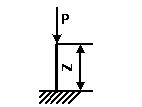
Расчет сжатого стержня на устойчивость.
1. Из условия устойчивости определить размеры поперечного сечения.
2. Определить величину критической силы.
3. Найти коэффициент запаса устойчивости. R = 180 МПа
Р = 300 кН;
L = 2,3 м.
 |
R= 180МПа.
 |
Решение:
При расчетах сжатых стержней на устойчивость применяется формула:
 |
где φ – коэффициент уменьшения основного допускаемого напряжения, определяемый по таблице в зависимости от материала и гибкости стержня.
Подбор сечения заданной формы выполняем методом последовательного приближения, выбирая в качестве первого приближения φ = 0,2:
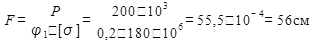
Запишем формулу площади сечения, выразив ее через основной размер «а»:
F = 1,5a 2
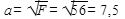
Приравнивая полученные значения площади, имеем:
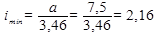
Гибкость стержня вычисляем по формуле: 
Где μ – коэффициент приведенной длины, зависящий от способа закрепления концов стержня. В данном случае μ = 2:
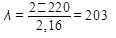
λ = 200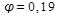 
λ = 210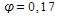 
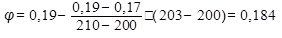
Ошибка составляет: 
Во втором приближении принимаем φ равным среднеарифметическом результату двух предыдущих значений:
Гибкость стержня:
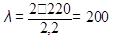
λ = 200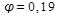
Ошибка составляет: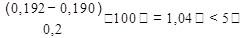 
Поскольку ошибка расчета меньше 5%, принимаем окончательно а = 7,6 cм.
Найдем величину критической силы и коэффициента запаса устойчивости.
Величина критической силы определяется исходя из 
:
для стержней большой гибкости λ≥λ пред (200 ≥100 ), величина критической силы определяется по формуле Эйлера:
кН.
Коэффициент запаса устойчивости находится как отношение критической нагрузки к действительной:
|
|
|
