Задание 2. Дисперсионный анализ

Контрольная работа по предмету «Методы анализа данных на ЭВМ»

 

 

Сделала: Китаева В.Е. И-8-7

Проверил: Казаков Д.

 

 

Москва

Задание №1

Даны 3 выборки по 50 элементов. Законы распределения: нормальный для 1 выборки и равномерный для 2 выборок. Провести анализ выборок. Провести проверку однородности выборок с помощью критерия Вилкоксона.

Критерий Вилкоксона — непараметрический критерий, используемый для проверки различий между двумя выборками парных измерений. Критерий предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, то есть, способен определить, является ли сдвиг показателей в одном направлении более интенсивным, чем в другом. Критерий применим в тех случаях, когда признаки измерены, по крайней мере, в порядковой шкале. Суть метода состоит в том, что мы сопоставляем абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.

 

1. Задаем параметры нормального распределения: медиану и отклонение.

И параметры равномерного распределения – координаты отрезка.

2. Статистика/описательная статистика/замечаем расхождение в медианах

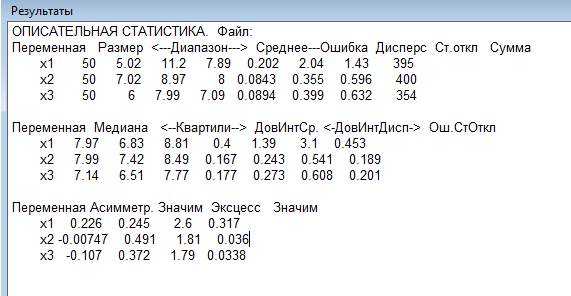
3. Статистика/гистограмма нормальность. Замечаем сильное расхождение в законах распределения по критерию хи-квадрат.

X1:

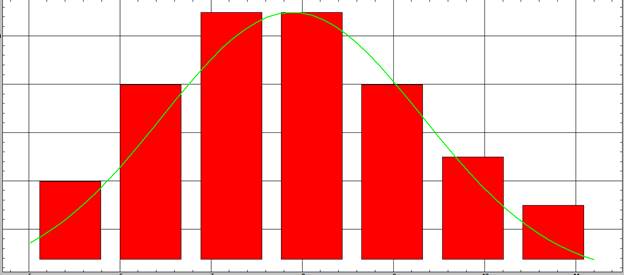
X2:

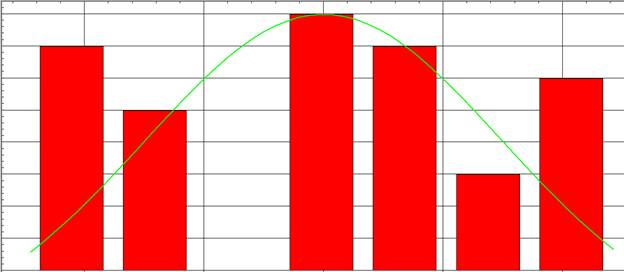
X3:

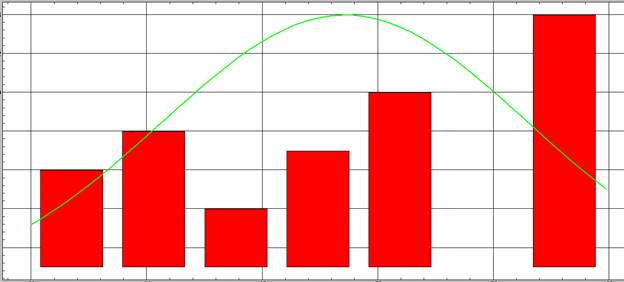
4. Проведем корреляционный анализ. Статистика – параметрическая корреляция.

Если коэффициент корреляции равен нулю, то зависимости нет.

5.Статистика/Непараметрические тесты, сдвига положения.

Переносим выборки.

 

Результаты:

КРИТЕРИИ СДВИГА (ПОЛОЖЕНИЯ). Файл:

 

Переменные: x1, x2

Вилкоксон=2.6E3, Z=-0.496, Значимость=0.31, степ.своб = 50,50

Гипотеза 0: <Нет различий между медианами выборок>

 

Для парных данных:

Вилкоксон=667, Z=0.285, Значимость=0.388, степ.своб = 2,50

Гипотеза 0: <Нет различий между медианами выборок>

 

Переменные: x1, x3

Вилкоксон=3.18E3, Z=-4.53, Значимость=2.95E-6, степ.своб = 50,50

Гипотеза 1: <Есть различия между медианами выборок>

 

 

Для парных данных:

Вилкоксон=1.07E3, Z=4.19, Значимость=1.38E-5, степ.своб = 2,50

Гипотеза 1: <Есть различия между медианами выборок>

 

 

Переменные: x2, x3

Вилкоксон=3.51E3, Z=-6.81, Значимость=5.46E-12, степ.своб = 50,50

Гипотеза 1: <Есть различия между медианами выборок>

С поправкой Бонферрони: крит.значимость=0.0167

Гипотеза 1: <Есть различия между медианами выборок>

Ван дер Варден=32.1, Z=6.65, Значимость=1.55E-11, степ.своб = 50,50

Гипотеза 1: <Есть различия между медианами выборок>

 

Для парных данных:

Вилкоксон=1.25E3, Z=5.95, Значимость=1.37E-9, степ.своб = 2,50

Гипотеза 1: <Есть различия между медианами выборок>

 

Делаем вывод о том, что выборки x1 и x2 однородны.

И действительно, медиана x2=(7+9)/2=8=медиане x1. А медиана x3=7.

 

Задание 2. Дисперсионный анализ

Даны 5 выборок по 50 элементов. Законы распределения: нормальный для 3 выборок и равномерный для 2 выборок.

Провести анализ выборок. Проверить влияние фактора на отклик, используя дисперсионный анализ.

Дисперсионный анализ показывает степень влияния факторов на отклик, т.е. на значение измеряемого признака. В зависимости от количества факторов анализ – однофакторный, двухфакторный и т.д.Идея дисперсионного анализа состоит в том, что дисперсия отклика различается на сумму составляющих её дисперсий.

 

1.Добавляем к предыдущим выборкам две с нормальным распределением.

2. Переносим.

3. Статистика/Согласие распределений. Замечаем что все распределения нормальные.

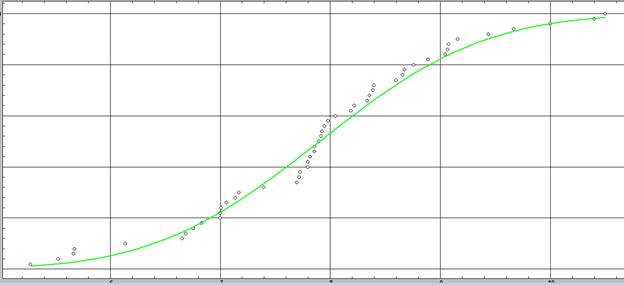
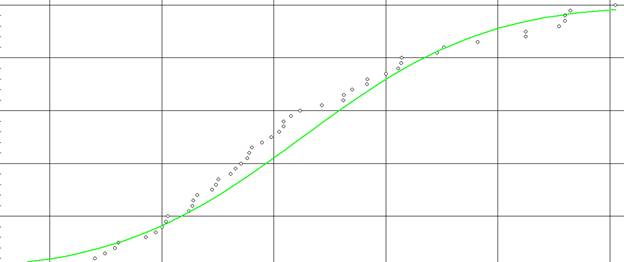
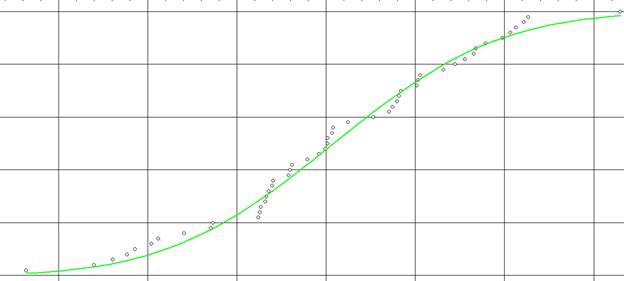
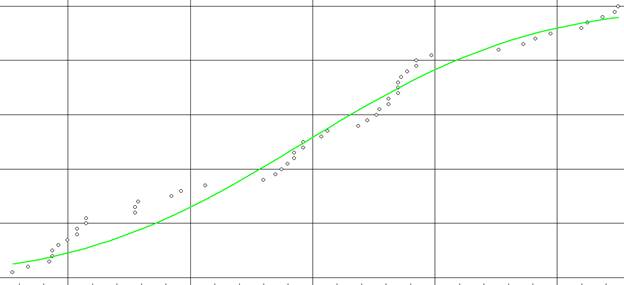
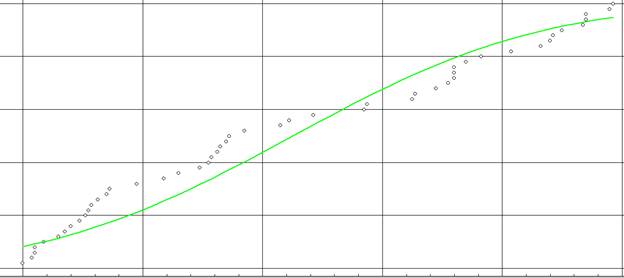
4. Так как распределения нормальные, выбираем параметрический метод.

 

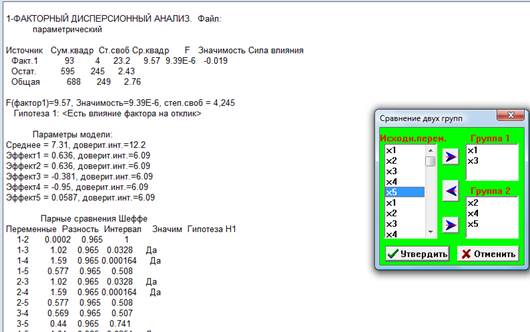
Исходя из того, что x4 встечается в обоих случаях, когда гипотеза существует, то x4-фактор, а остальные x –отклики.

 

 

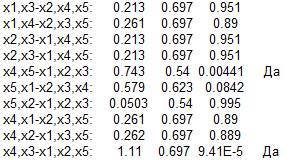
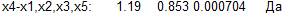
4. Но если делать проверку на нормальность через Статистика/гистограмма нормальность, то

Значит, используем непараметрический метод Фридмана.

Задание № 3

Даны 3 выбороки по 20 элементов. Закон распределения нормальный.

Провести анализ выборок. Проверить влияние фактора на отклик, используя критерий Джонкхиера.

 

Когда пользователю заранее известно, что имеющаяся группа результатов упорядочены по возрастанию фактора А, то можно использовать критерий Джонкхиера, более чувствительный (более мощный) к влиянию фактора.

Критерий Джонкхиера основан на статистике Манна-Уитни U_u,v.

Критерий Манна- Уитни повторяет основные идеи критерия знаков и в определенном смысле является его продолжением. Он основан на по парном сравнении результатов из первой x₁,x₂,…,x_n выборки и второй y₁,y₂,…,y_m выборки. Если x_i <y_j, то S(x_i, y_j)=1, если x_i>y_j, то S(x_i, y_j)=0. Изменяя i от 1 до m и j от 1 до n, получаем m*n парных сравнений. Величина 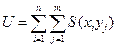называется статистикой Манна-Уитни.

Для каждой пары натуральных чисел U и V, где 1≤U<V≤m обозначают номера столбцов, составляют статистику Манна-Уитни. Статистка Джонкхиера определяется как:

 

1. В данном случае используем только целые числа.

2. Выбираем: ”Статистика/Дисперсионный анализ –однофакторный”, переносим все выборки.

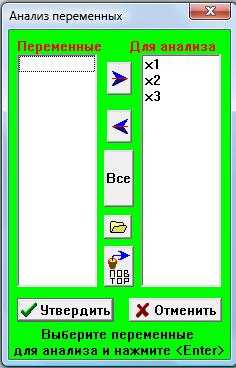
3. Упорядиваем значения 1-го фактора, чтобы среди результатов был критерий Джонкхиера.

Прежде чем судить о количественном влиянии фактора на измеряемый признак, нужно

выяснить есть ли такое влияние вообще. По результатам мы видим, что его нет,

значит, все данные таблицы принадлежат одному и тому же распределению и

выборки однородны.

 

Задание № 4. Модели случайной компоненты (случайный процесс и когда можно говорить о том, что случайный процесс задан, Гауссовский случайный процесс, Марковский случайный процесс, белый шум, процесс скользящего среднего n-го порядка, процесс авторегрессии n-го порядка).

Обычно вариационный ряд не удаётся полностью описать одной лишь детерминированной компонентой, в нём присутствует и случайная компонента.

Случайный процесс X(t) задан, если для каждого t из T определена функция распределения X(t):

F_t(x)=P(X(t)≤x),

 

и для любого конечного числа элементов 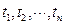из множества 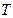определена 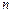-мерная функция распределения величины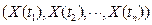

.

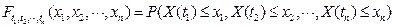При этом распределения должны быть согласованы в том смысле, что «старшие» распределения определяют «младшие».

 

Важным классом случайных процессов являются нормальные (гауссовские) случайные процессы. Для полного описания нормальных случайных процессов достаточно указать его двумерное нормальное распределение.

 

 

Белым шумом называют временной ряд (случайный процесс) с нулевым средним, если составляющие его случайные величины X(t) независимы и распределены одинаково (при всех 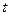). Независимость двух случайных величин определяется как .

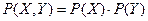Процесс скользящего среднего n-го порядка называется процесс:

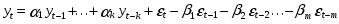
k – порядок авторегрессии; т – порядок скользящего среднего.

 

Процессом авторегрессии (AR) n-го порядка со средним значением µ называют случайный процесс :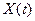

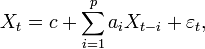
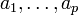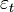где — параметры модели (коэффициенты авторегрессии), -постоянная (часто для упрощения предполагается равной нулю), а — белый шум.

 

Поведение многих процессов в будущем определяется только их состоянием в настоящем и воздействиями на процесс, которые будут оказываться в будущем. А предыдущие процессы называются марковскими.

Случайная последовательность 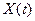, 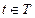называется марковской, если для любых А,В и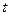

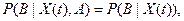
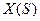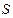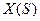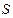
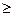
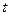где – А- произвольное событие, выраженное через случайные величины , где ≤t-1, а В- произвольное событие, относящееся к будущему В- выражается через случайные величины , где +1/

 

Задание № 5. Автокорреляционная функция. Частная автокорреляционная функция. Вид коррелограммы при наличии во временном ряде тренда, сезонной компоненты. Коррелограмма белого шума, процесса скользящего среднего, авторегрессии, авторегрессии 2го порядка.

 

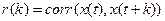Автокорреляционная функция. Автокорреляционной функцией стационарного процесса называют функцию , где 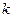>0-целое число.

Величину 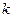часто называют задержкой или лагом.

 

ЧАКФ полезна, когда по наблюдаемому отрезку временного ряда мы пытаемся подобрать для его описания подходящую - модель. Подобно автокоррекционной функции, ЧАКФ определяется для каждого натурального 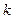и представляет собой бесконечную последовательность. Её элементы мы обозначим как .

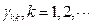Если в стационарном временном ряде авторегрессия имеет порядок . то мы, используя уравнения Юла-Уолкера, можем определить все 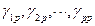. Из этого набора чисел нам нужно всего одно число 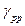- это число ЧАКФ.

 

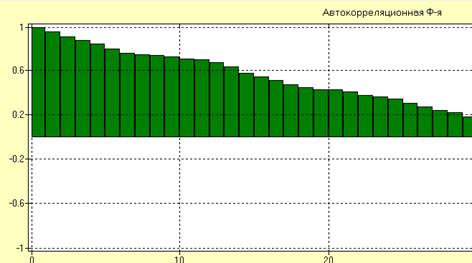
Для проверки стационарности ряда остатков и оценки его дисперсии на практике чаще всего используется выборочная автокорреляционная функция (коррелограмма) и частная автокорреляционная функция.

Для временного ряда, содержащего тренд, коррелограмма не стремится к нулю с ростом лага .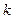

Для ряда с сезонными колебаниями коррелограмма также будет содержать периодические всплески, соответствующие периоду сезонных колебаний. Это позволяет устанавливать предполагаемый период сезонности после удаления из временного ряда линейного тренда.

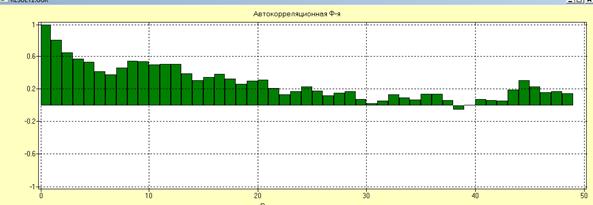
Автокорреляционная функция 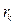белого шума равна 0 для всех .

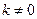Коррелограмма процессов скользящего среднего.

Пусть 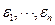-гауссовский белый шум. Обозначим через 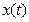процесс скользящего среднего первого порядка с коэффициентом 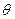и средним равным 0

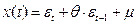или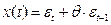

В этом процессе зависят между собой только соседние значения 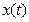и 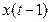. При этом их корреляция 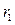равна:

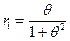
Корреляция процессов авторегрессии: пусть 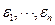- гауссовский белый шум. Общий вид уравнения авторегрессии первого порядка:

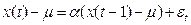
Процесс авторегрессии с нулевым средним задаётся, как

, где 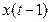не зависит от . Члены этого процесса не становятся независимыми с ростом промежутка времени между ними. Однако при определённых условиях на коэффициенты эта зависимость быстро убывает.

Уравнение авторегрессии второго порядка:

 

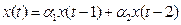
Задание №6

Осуществить прогноз на 20 точек.

График временного ряда.

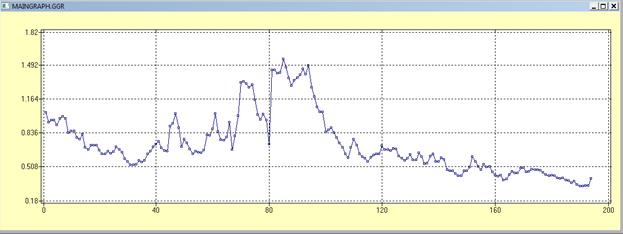
Для прогноза надо свести временной ряд к стационарному. В теоретических исследованиях и практических задачах важную роль играют последовательности случайных величин, вероятностные свойства которых не изменяются во времени. Такие случайные последовательности называют стационарными.

После удаления детерминированной компоненты(тренд, циклическая, сезонная составляющая) временной ряд должен свестись к стационарному процессу.

1. Определим наличие сезонности и ее период T_сез.

Сезонная компонента отражает присущую миру и человеческой деятельности повторяемость процессов во времени. Она состоит из последовательности почти повторяющихся циклов.

 

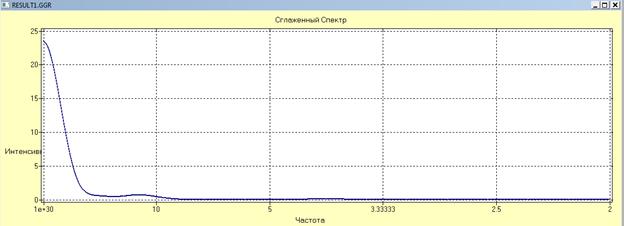
Выбираем метод/спектральный анализ/ сглаженная периодограмма:

{тип шкалы – периодический};

T_сез = максимальному выбросу на графике

Выбираем граф/XY координаты, находим T_сез =23.

2. Удаление сезонной составляющей

Для удаления сезонной составляющей с помощью разностных операторов есть: метод наименьших квадратов и метод сезонных разностей. Для мультипликативной модели эта процедура сводится к делению значений исходного ряда на соответствующие сезонные индексы.

 

Выбираем предварительный анализ/сез. компонента

{Мультипликативная, т.к. амплитуда убывает

Сезонность устранена}

Результат: остались тренд и случайная составляющая.

Сохраняем результат, добавляем в таблицу.

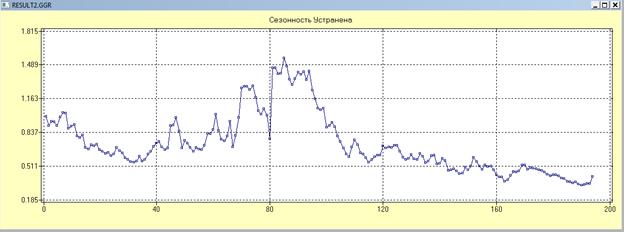
3. Удаление тренда

Трендом временного ряда при 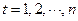называют плавно изменяющуюся не циклическую компоненту, описывающую влияние долговременных факторов, эффект которых сказывается постепенно.

 

Выбираем метод/предварительный анализ/разности {1 порядок}

Результат/сохранить и добавить в таблицу

Полученный ряд – только случайная составляющая.

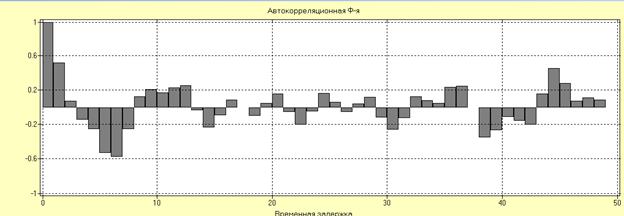
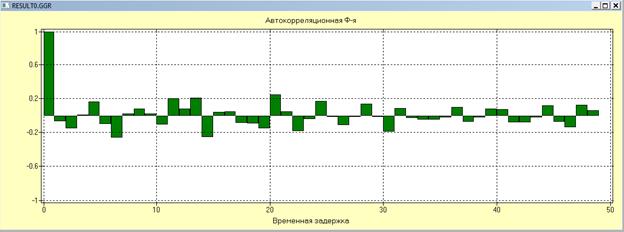
4. Проверяем ряд с остатками на стационарность.

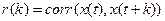Автокорреляционной функцией стационарного процесса называют функцию , где 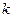>0-целое число.

Величину 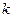часто называют задержкой или лагом.

 

 

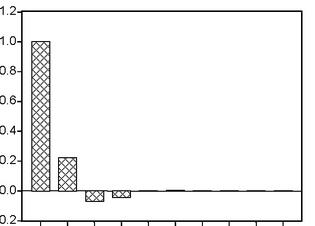
5. Определяем порядок авторегрессии (для случайной составляющей)

Выбираем Метод/ARCC-модели/порядки AR модели (машинный способ)

Отсюда запоминаем что AR-порядок 0, СС-порядок - 6

 

6. Строим модель для случайной составляющей

Выбираем метод/ARCC-модели/AR-модель {выбор порядка вручную, спектральная плотность периодическая}

Сохраняем полученную модель.

 

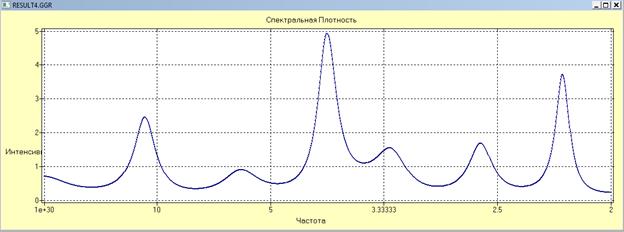
7. Строим результат полученной модели через прогнозирование

Это нужно для проверки порядков выбранной модели.

Выбираем метод/прогнозирование/ARCC-прогнозирование {порядок разностей 0} и модель.

 

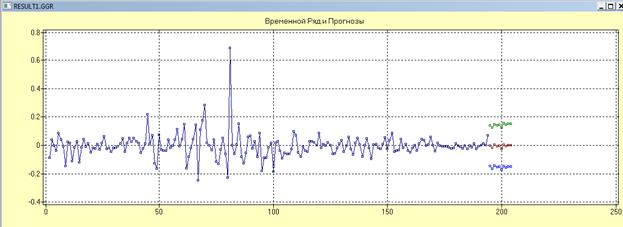
8. Прогноз исходного ряд

Выбираем метод/ARCC-модель/сезонная ARCC-модель

AR-порядок 1 СС 0

сез. AR-порядок 1 Сез. СС 0

Период = 23, периодическая шкала.

Сохраняем модель 2.

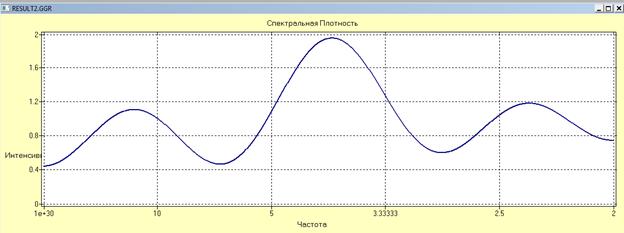
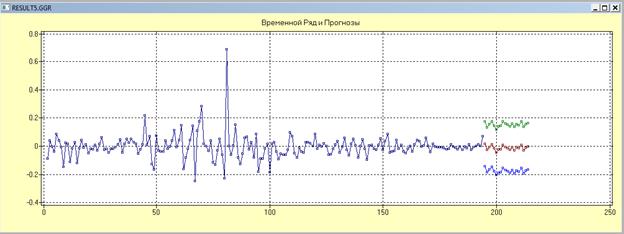
9. Метод/прогнозирование/сез. ARCC-прогнозирование {порядок разностей 0; сезонные разности 1; модель 2}

Количество прогнозов выбираем =20.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: