 |
Для цепей с индуктивностями
|
|
|
|
t = L/R Э. (6.4)
для цепей с емкостями
t = R Э C, (6.5)
где R Э – входное сопротивление цепи, из которой удалены все источники, относительно зажимов реактивного элемента.
Связь между постоянной времени t и корнем характеристического уравнения p задается зависимостью p = – 1 / t.
Принуждённая составляющая совпадает со значением искомой величины тока (напряжения) в новом установившемся (стационарном) режиме, наблюдающемся в послекоммутационной цепи после окончания переходного процесса. Таким образом, расчет принужденной составляющей производится любыми известными методами расчета стационарных режимов в линейных электрических цепях постоянного или переменного тока в зависимости от вида источников. При расчете цепей на постоянном токе следует помнить, что сопротивление идеальной емкости постоянному току бесконечно, а сопротивление идеальной индуктивности постоянному току равно нулю.
Расчет постоянной интегрирования A ведется с учетом начальных (граничных) условий.
Согласно правилам коммутации
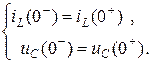(6.6)
Значения iL (0–)или uC (0–) в докоммутационной цепи (считается, что до коммутации в цепи был установившийся режим) и определяют независимые начальные условия.
Прочие величины не подчиняются правилам коммутации, поскольку в момент коммутации t = 0 возможно их скачкообразное изменение. Поэтому необходимо также остановиться на правилах определения значений таких величин в момент t = 0+, являющихся зависимыми начальными значениями.
Существуют два способа определения значений величин, не подчиняющихся правилам коммутации, в момент t = 0+.
Первый способ связан с составлением системы уравнений Кирхгофа для послекоммутационной цепи. В полученную систему подставляется момент t = 0+, и искомая величина выражается через известные независимые начальные условия: емкостное напряжение uC (0+), если расчетная цепь содержит емкость, или через индуктивный ток iL (0+), если цепь содержит индуктивность. В случае разветвленной цепи путь довольно трудоемкий.
|
|
|
Второй способ основан на построении схемы замещения [2] в 0+ в соответствии со следующими правилами:
а) источники и резисторы остаются на своих местах без изменений;
б) индуктивности с нулевыми начальными условиями (iL (0–) = 0) заменяются на обрыв цепи; с ненулевыми начальными условиями (iL (0–) ¹ 0) – на содействующие источники тока с задающим током JL = iL (0–);
в) емкости с нулевыми начальными условиями (uC (0–) = 0) заменяются на замыкающий накоротко провод; с ненулевыми начальными условиями (uC (0–) ¹ 0) – на противодействующие источники напряжения с задающей ЭДС ЕС = = uC (0–).
В результате получается простая резистивная цепь, в каждой ветви которой течет ток, значение которого совпадает с соответствующим током i (0+), а между любыми точками приложено напряжение u (0+). Расчет данной цепи любым известным методом позволит определить значение искомой величины в момент 0+.
Полученное значение искомой величины в момент t = 0+ позволяет определить неизвестную постоянную интегрирования. Для этого записывается полное решение
i (t) = iпр + Aept (6.7)
для момента времени t = 0+ и составляется уравнение
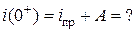(6.8)
В правой части уравнения (6.8) подставляется значение 
, полученное при помощи системы уравнений Кирхгофа в t = 0+ или схемы замещения для момента времени t = 0+
. (6.9)
В завершение работы следует построить график изменения искомой величины во времени. Единица масштаба по временной оси выбирается в соответствии с величиной постоянной времени переходного процесса:
(6.10)
При этом принимается во внимание то обстоятельство, что время переходного процесса t пп» (3 ¸ 5)t.
|
|
|
Таким образом, алгоритм расчета переходных процессов в цепях первого порядка следующий.
1. Расчет докоммутационного режима (t = 0-): определение в RC -цепи напряжения uC (0–), а в RL -цепи тока iL (0–), значения которых находятся любыми известными методами расчета цепей постоянного или переменного тока.
2. Запись полного решения в общем виде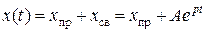 
.
3. Определение принужденной составляющей 
по виду цепи в новом стационарном (установившемся) режиме любыми известными методами расчета цепей постоянного или переменного тока.
4. Определение корня характеристического уравнения любым из перечисленных методов:
· алгебраизация дифференциального уравнения цепи;
· входного сопротивления (проводимости);
· главного определителя;
· с помощью постоянной времени.
5. Определение постоянной интегрирования при помощи
· системы уравнений Кирхгофа в 0+;
· схемы замещения в 0+.
6. Запись окончательного решения.
7. Построение графика изменения искомой величины x (t) в переходном режиме.
Пример расчета
Дана цепь (рис. 6.2) с параметрами E = 200 B, R1 = R3 = R5 = 100 Ом,
R 2 = R 4 =400 Oм, L = 0,2 Гн.
Определить закон изменения тока i 4(t) в переходном режиме при условии, что срабатывание ключей происходит в моменты времени:
1) K 1 в t = 0,
2) K 2 в t = 2t1, где t1– постоянная времени цепи, образованной в результате первой коммутации.
Решение
Первая коммутация
Расчет докоммутационной цепи (рис. 6.3). Следует помнить, что индуктивность в цепях с источниками постоянных воздействий представляет собой короткозамкнутый участок.
1. Запишем правила (законы) ком-мутации:
,
индуктивный ток
, 
после подстановки численных значений
,
искомый ток в докоммутационном режиме
Расчет послекоммутационной цепи
2. Запишем полное решение в виде суммы принужденной и свободной составляющей:
.
3. Расчет принужденной составляющей.
Цепь в принужденном режиме будет иметь вид, представленный на рис. 6.4.
,
.
4. Определение корней характеристического уравнения
4.1. Составим характеристическое уравнение по методу входного сопротивления (рис. 6.5):
,
.
4.2. Проверим правильность полученных результатов методом, основанным на определении постоянной времени цепи.
Для индуктивной цепи первого порядка t = L/R Э, где R Э – эквивалентное сопротив-ление пассивной цепи, полученной из рассматриваемой путем удаления источников, относительно зажимов реактивного элемента (в нашем случае индуктивности). Правило удаления источников: ветви с источниками тока обрываются, источники напряжения замыкаются накоротко.
|
|
|
В нашем случае пассивная цепь имеет вид (см. рис. 6.6):
t = L/R Э = 0,2/542,857 = 0,368мc.
Следовательно, p = –1/t = –1/0,368 = 2714,286 c-1.
5. Определение постоянной интегрирования.
Схема замещения в момент времени 0+ представлена на рис. 6.7, а, где JL 1 = iL (0 –) = 0,345 A.
Определим ток i 4(0 +) методом наложения. По схеме (рис. 6.7, б)
 |
По схеме (рис. 6.7, в)
.
,
.
Полный ток
.
Таким образом,
.
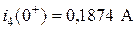Определим постоянную интегрирования:
i 4(0+) = 0,211+ A 1 = 0,1874; A 1 = – 0,0236.
Таким образом,
i 4(t) = 0,211 – 0,0236 e –2714 t
на промежутке t = (0+, t k2), где t = 0+ – момент первой коммутации.
Вторая коммутация
Для расчета переходных процессов в цепи после второй коммутации введем дополнительную переменную t 1 = t – 2t1.
Расчет докоммутационной цепи
1.Определим независимые начальные условия для второй коммутации (рис. 6.8).
.
Определим закон изменения iL (t) после первой коммутации (см. расчет первой комму-тации):
,
,
,
.
С помощью правил коммутации определим постоянную интегрирования:
,
0,263 + A 2 = 0,345, A 2 = 0,082.
Следовательно,
.
Для второй коммутации
.
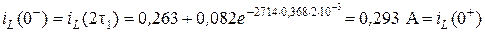Расчет послекоммутационной цепи
2. Определение корней характеристического уравнения
Составим характеристическое уравнение методом входного сопротивления (рис. 6.9):
,
.
3. Запишем полное решение:
.
4. Расчет принужденной составляющей (рис. 6.10):
,
,
, 
.
5. Расчет свободной составляющей. Схема замещения в t 1 = 0+ для второй коммутации имеет вид (рис. 6.11), на которой величина задающего тока источника тока
.
Определим ток i 4(0+) методом наложения (рис. 6.12).
Составляющая от действия источника ЭДС (см. рис. 6.12, а):
.
Составляющая от действия источника тока (см. рис. 6.12, б):
Полный ток
.
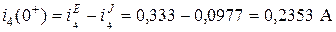Определим постоянную интегрирования:
i 4(0+) = 0,25 + A 3 = 0,2353; A 3 = – 0,0147.
Таким образом,
|
|
|
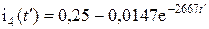
для промежутка времени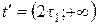 
.
Итак, закон изменения тока после срабатывания первого коммутатора
i 4(t)1 = 0,211 – 0,0236e–2714 t
после срабатывания второго коммутатора
i 4(t 1)2 = 0,25 – 0,0147e–2667 t ¢, где t 1 = t – 2t1.
На рис. 6.13 изображен график изменения i 4(t) в переходных режимах после срабатывания первого и второго коммутаторов.
|
|
[1] Что эквивалентно приравниванию нулю задающих воздействий (параметров) источников, т.е. исключению источников из цепи.
[2] Схемная реализация системы уравнений Кирхгофа, составленной для момента t =0+
|
|
|
