 |
Процесс коммутации тока вентилями в простой нулевой
|
|
|
|
m -пульсовой схеме выпрямления. Влияние процесса коммутации
на показатели выпрямителя
При рассмотрении электромагнитных процессов в m-пульсовой нулевой схеме выпрямления принимались следующие допущения: процесс коммутации принимался мгновенным (рис. 7, в), то есть трансформатор и вентили принимались идеальными, а индуктивные сопротивления Хd = ∞ и Xв = 0. При Xв = 0 Lтр=0 и Lс=0.
При значениях индуктивностей трансформатора Lтр и сети Lс, отличных от нуля, коммутация вентильных токов мгновенной быть не может, так как индуктивность, сосредоточенная в цепи протекания тока, создает противоЭДС (ЭДС самоиндукции).
(30)
При этом, начиная с момента равенства мгновенных значений фазных напряжений вентильных обмоток (точка 2 на рис. 7, е), ток в цепи вентиля VD1 будет постепенно уменьшаться до нуля, а в цепи вентиля VD2 – возрастать до значения Id (рис. 7, з):
(31)
(32)
Время одновременной работы двух вентилей (при прекращении работы одного и вступлении в работу другого) называется временем коммутации, а угол, пропорциональный этому времени – углом коммутации γ.
В интервале времени, равном γ, в рассматриваемых схемах открыты два вентиля, что равносильно короткому замыканию двух фаз вторичной обмотки трансформатора.
Закон изменения тока в период коммутации можно получить, воспользовавшись методом суперпозиции (наложения).
При этом рассматриваются следующие токи (рис. 12):
– токи, протекающие через нагрузку и две обмотки трансформатора
Id=I’d+I”d; (33)
|
|
|
– ток, протекающий через две обмотки трансформатора и два вентиля – ток коммутации iK.
Фактические токи в вентилях будут равны:
(34)
Ток коммутации возникает за счет разности фазных ЭДС вентильных обмоток ΔUк. Векторная диаграмма, поясняющая причину возникновения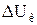 
, приведена на рис. 13.
Рис. 12. Контуры протекания токов при рассмотрении процесса коммутации
Рис. 13. Векторная диаграмма, поясняющая причину возникновения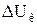 
На рис. 13 
и 
– векторы фазных ЭДС коммутирующих фаз.
Из треугольника АВС:
(35)
Амплитудное значение
(36)
Мгновенное значение
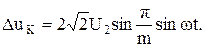(37)
Для упрощения полагаем, что:
– активные сопротивления трансформатора и питающей сети равны нулю (Rтр = 0; Rс = 0);
– индуктивность трансформатора и питающей сети сосредоточены в цепи вентильной обмотки, то есть приведены к напряжению вентильной обмотки.
Тогда ток iК, протекающий через две фазы вентильной обмотки, будет равен:
(38)
В этом выражении учтено отставание тока коммутации iК на 90о от напряжения в цепи с индуктивным сопротивлением.
Ранее получена система уравнений (34), из нее:
; (39)
(40)
Отметим граничные условия режима коммутации (рис. 14)
Рис. 14. Характер изменения токов 
и 
на интервале коммутации
При ωt=0: iVD1 = Id, iVD2 = 0.
Из выражений (39) и (40) с учетом (38) имеем:
; (41)
. (42)
Подставив (38), (41) и (42) в (39) и (40), получим:
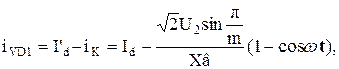(43)
(44)
При ωt = γ (рис. 14): iVD1 = 0, iVD2 = Id.
Из выражения (44) имеем:
; (45)
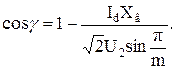(46)
|
|
|
По выражениям (43) и (44) можно определить и построить вентильные токи в период коммутации, а по выражению (46) рассчитать продолжительность процесса. С увеличением тока и сопротивления цепи значение угла γ растет, а с ростом напряжения U2 – уменьшается.
Определим мгновенное значение выпрямленного напряжения ud в период коммутации вентильных токов. Кривые фазных напряжений коммутирующих фаз приведены на рис. 15.
Рис. 15. Кривые фазных напряжений коммутирующих фаз выпрямителя
Так как ЭДС самоиндукции es = | esa | = | esb |, то
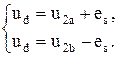(47)
Откуда
. (48)
Таким образом, в период коммутации мгновенное значение выпрямленного напряжения равно полусумме мгновенных значений напряжений коммутируемых фаз (см. рис. 15 и 7, е).
Явление коммутации приводит к:
– снижению среднего значения выпрямленного напряжения на значение 
;
– искажению формы кривой выпрямленного напряжения, а, следовательно, к изменению его гармонического состава;
– уменьшению среднего значения выпрямленного напряжения.
Из-за процесса коммутации уменьшается среднее значение выпрямленного напряжения:
(49)
В соответствии с рис. 15 определим потери на коммутацию:
(50)
Учитывая (45), имеем
. (51)
Уравнение внешней характеристики выпрямителя имеет вид:
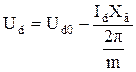. (52)
Ранее было получено выражение (29) для определения 
, с учетом
(53)
Уравнение внешней характеристики может быть представлено
(54)
Введем обозначение: 
– коэффициент наклона внешней характеристики. С учетом этого
(55)
или в относительных единицах
(56)
Для трехфазных выпрямителей
. (57)
В соответствии с (57) для шестипульсовых выпрямителей А = 0,5, для двенадцатипульсовых А = 0,26, для двадцатичетырехпульсовых А = 0,13 и т.д.
Внешней характеристикой выпрямителя называется зависимость среднего значения выпрямленного напряжения от среднего значения тока нагрузки Ud = f (Id).
|
|
|
Очевидно, чем меньше значение коэффициента А, тем меньше потери на коммутацию, тем стабильнее уровень напряжения и лучше схема выпрямления.
Внешняя характеристика нулевого выпрямителя в относительных единицах представлена на рис. 16.
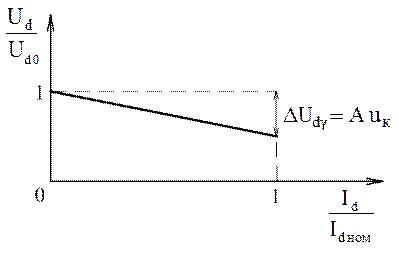
Рис. 16. Внешняя характеристика нулевого выпрямителя
Коммутация тока повлияет и на условия работы вентилей. При сохранении токового режима и величины максимального обратного напряжения последнее в момент окончания коммутации (рис. 17) восстанавливается скачком до величины
UVD0 = UVD max sin γ, (58)
что несколько утяжеляет условия работы вентилей.
а
б
Рис. 17. Кривая выпрямленного (а) и обратного (б) напряжения
на вентиле с учетом процесса коммутации
Из-за процесса коммутации форма потребляемого тока преобразователя изменяется в лучшую сторону, но из-за появления сдвига относительно кривой напряжения уменьшается значение коэффициента мощности и снижаются энергетические показатели выпрямителя.
3. Сложные нулевые схемы выпрямления
Любая сложная схема выпрямления – результат параллельного или последовательного соединения простых схем. Рассмотрим следующие сложные схемы выпрямления.
|
|
|
