Качество выпрямленного напряжения

 

Кривая выпрямленного напряжения является пульсирующей кривой. Для нулевых схем – это огибающая максимальных фазных напряжений (рис. 19), для мостовых – максимальных линейных.

Рис. 19. Кривая выпрямленного напряжения m-пульсового нулевого

 выпрямителя () и переменная составляющая () этого напряжения

в режиме холостого хода

 

     Кривая выпрямленного напряжения для любой m-пульсовой схемы в пределах одной пульсации с периодом Т_пульс = 2π/m выражается функцией

                                        (11)

где а – коэффициент схемы, равный отношению амплитуды выпрямленного напряжения к амплитуде фазового.

     Для двухполупериодных нулевой и мостовой схем и трехпульсовой нулевой схемы a = 1; для шестипульсовой нулевой схемы параллельного типа a = 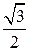; для шестипульсовой мостовой схемы a = .

     Уравнение (11) справедливо только в пределах одной пульсации напряжения в режиме холостого хода.

Выпрямленное напряжение является периодической функцией и состоит из постоянной составляющей U_d0, численно равной среднему значению, и переменной составляющей u_d0ν, представляющей сумму высших гармонических составляющих:

                                           (12)

Разложение кривой выпрямленного напряжения на постоянную составляющую и гармоники производится с помощью ряда Фурье.

Кривая выпрямленного напряжения симметрична относительно оси ординат, то есть является четной функцией, и при разложении ее в ряд Фурье синусные коэффициенты (b_n) равны нулю, т.е.:

                      (13)

или с учетом того, что угловая частота пульсации

                                                (14)

получим

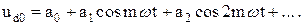                 (15)

В выражениях (13) и (15) а₀ – постоянный член ряда Фурье, определяемый по выражению:

                               (16)

Для неуправляемого выпрямителя:

          (17)

для управляемого выпрямителя:

                                           (18)

для инвертора:

                                           (19)

Переменная составляющая  представляет собой сумму ряда высших гармоник, порядок (номер) которых обозначается n.

Так как порядок гармоники n выражается относительно кривой питающего напряжения, то:

                                                (20)

где  Т_пит = 2π – период питающего напряжения;

Т_n – период гармоники n-го порядка.

В кривой выпрямленного напряжения могут содержаться только те гармоники, период которых укладывается целое число раз l в интервале одной пульсации.

Следовательно

                                                (21)

где – число пульсаций в кривой выпрямленного напряжения;

l – ряд целых чисел.

Из этого следует, что порядок n-ой гармоники определяется по выражению:

                                   (22)

Таким образом, в кривой выпрямленного напряжения любого преобразователя (неуправляемого или управляемого выпрямителя, зависимого инвертора) содержатся гармоники, порядковые номера которых кратны числу пульсаций в кривой выпрямленного напряжения m. Такие гармоники получили название канонических.

Приведем примеры:

– при m = 2    n = 2, 4, 6, 8, …;

– при m = 3    n = 3, 6, 9, 12, …;

– при m = 6    n = 6, 12, 18, 24, …;

– при m = 12    n = 12, 24, 36, 48, …;

– при m = 24    n = 24, 48, …;

– при m → ∞    n → ∞.

Значение амплитуды n-ой гармоники:

       (23)

В относительных единицах амплитудное значение n-ой гармоники:

                                         (24)

Действующее значение n-ой гармоники:

                                            (25)

Из этих выражений видно, что доля n-ой гармоники зависит лишь от ее порядкового номера. При увеличении числа пульсаций m уменьшается число гармоник, доля же каждой данной n-ой гармоники остается прежней.

Действующее значение n-ой гармоники любого преобразователя (неуправляемого или управляемого выпрямителя, зависимого инвертора) определяется по выражению:

                              (26)

амплитудное же значение n-ой гармоники будет в  раз больше.

     Для неуправляемого выпрямителя в выражении (26) следует принимать α = 0, для управляемого выпрямителя α ≠ 0, для зависимого инвертора α = ß.

Действующее значение переменной составляющей выпрямленного напряжения при холостом ходе:

                    (27)

Основным критерием, характеризующим относительную величину переменной составляющей кривой выпрямленного напряжения, является коэффициент полной волнистости, то есть отношение эффективного (действующего) значения переменной составляющей к среднему значению выпрямленного напряжения.

Для неуправляемого выпрямителя коэффициент полной волнистости:

                                              (28)

для управляемого выпрямителя или зависимого инвертора:

                                           (29)

Приведем примеры значений для неуправляемых преобразователей:

– при m = 2 = 0,483;

– при m = 3 = 0,183;

– при m = 6 = 0,042;

– при m = 12 = 0,01;

– при m = 24 = 0,003;

– при m → ∞  → 0.

Приведенные значения свидетельствуют о преимуществе преобразователей с бóльшим числом пульсаций, так как из-за меньшей суммарной доли высших гармоник в кривой напряжения уменьшается влияние преобразователей на смежные линии связи, работу тяговых двигателей и рельсовых цепей.

Форма кривой напряжения при нагрузке при синусоидальном и симметричном питающем напряжении искажается из-за процесса коммутации. Кроме того, происходит искажение кривой из-за наличия угла α, но порядок гармоник, содержащихся в кривой, сохраняется (n =m l), так как период и продолжительность пульсаций не изменяются. Однако, доля гармоник несколько увеличится, так как теперь кривая выпрямленного напряжения не симметрична относительно оси ординат. В составе ряда Фурье для нее появятся и косинусные (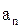), и синусные () члены.

Амплитуда гармоники в этом случае определяется как

                                                  (30)

 

 

123456

Поделиться:

Воспользуйтесь поиском по сайту: