Краткие теоретические сведения

Частотные свойства биполярного транзистора

Цель работы: исследование зависимости коэффициента усиления по току биполярного транзистора от частоты сигнала.

Краткие теоретические сведения

Одним из основных факторов, определяющим пригодность транзистора для использования в той или иной электрической схеме, является зависимость его параметров от частоты. Особенно большое значение имеют зависимости усилительных свойств транзистора от частоты. Известно, что уже на частотах в несколько сот килогерц сплавные триоды заметно теряют свои усилительные свойства. Наряду с этим, с увеличением частоты сигнала растет шунтирующее действие емкостей р - n переходов, особенно емкости коллектора, так как в этом случае шунтируется большое сопротивление коллекторного перехода, включенного в запирающем направлении.

В силу конечного времени пролета носителей через базу происходит фазовый сдвиг выходного сигнала относительно входного. Фазовый сдвиг между током эмиттера и током коллектора обусловлен тем, что изменения коллекторного тока происходят позднее вызвавших их изменений тока эмиттера на среднее время распространения процесса диффузии через базу t_D (рис. 1). Пока частота сигнала невелика и t_D << T (T – период повторения процесса), можно считать, что изменения тока эмиттера практически мгновенно следуют за изменениями тока эмиттера. С ростом частоты сигнала период T уменьшается и становится соизмеримым со временем диффузии. Чем больше толщина базы, тем больше время диффузии и больше сдвиг фаз между токами, чем в транзисторах с малым расстоянием между переходами.

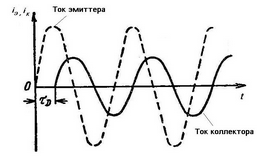
Рис. 1. Диаграмма фазового сдвига тока коллектора относительно тока эмиттера на среднее время диффузии t_D

Кроме того, в силу хаотичности диффузионного движения неосновных носителей зарядов в области базы они приходят на коллектор неодновременно, что вызывает искажение формы выходного сигнала и уменьшение коэффициента усиления по току с повышением частоты. Группа зарядов, одновременно вошедших в область базы, достигнет коллекторного перехода в разное время. Если предположить, что эмиттерный ток имеет вид короткого импульса с идеальным, мгновенно достигающим максимального значения фронтом и идеальным, мгновенно спадающим до нуля срезом, то ток коллектора таких фронтов иметь не будет. Из-за разницы в скорости движения зарядов, как фронт, так и срез импульса коллекторного тока окажутся растянутыми.

Если амплитуду импульсов тока в эмиттере принять за единицу, то из-за рекомбинации неравновесных носителей амплитуда импульсов коллекторного тока будет в α₀раз меньше. Временные диаграммы приращений токов эмиттера и коллектора Δ i_э и Δ i_к для этого случая представлены на рис. 2,а. Для большего удобства сравнения диаграмм временная диаграмма тока коллектора сдвинута по оси на время t_D, соответствующее среднему времени распространения. Для простоты время нарастания фронта импульса коллекторного тока до максимальной величины t ₁ считается равным времени спадания среза.

Рис. 2. Временные диаграммы приращений токов эмиттера и коллектора: а) низкая частота, α ≈ α₀; б) повышенная частота, α ≈ α₀; в) более высокая частота α₁ < α₀;. Диаграммы токов эмиттера и коллектора сдвинуты на среднее время диффузии t_D и совмещены для удобства сравнения.

Если уменьшить длительность импульсов и соответственно интервал между ними до величины, равной 2 t ₁ (рис. 2,б), то в этом случае форма импульса будет искажена более значительно, но величина импульса коллекторного тока останется по-прежнему равной α₀.

При дальнейшем уменьшении длительности импульсов и интервалов между ними величина импульсов коллекторного тока уменьшится до величины α₁ при неизменной величине импульсов эмиттерного тока, как показано на рис. 2, в.

Аналогичная картина будет наблюдаться и в случае синусоидального сигнала. Следовательно, различие в тепловых скоростях зарядов, распространяющихся диффузионно, с ростом частоты приводит к уменьшению амплитуды тока периодического сигнала в коллекторе. При неизменной амплитуде тока эмиттера это равносильно падению величины коэффициента передачи тока.

Так как коэффициент передачи тока биполярного транзистора α в схеме с общей базой представляет собой отношение тока сигнала в цепи коллектора к току сигнала в цепи эмиттера, то, следовательно, α зависит от частоты и характеризуется модулем |α| и фазой φ:

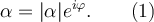
Частота входного сигнала, при которой модуль коэффициента передачи уменьшается в √2 раз по сравнению со статическим значением α₀, называется предельной частотой усиления по току ω_α в схеме с общей базой.

Статический коэффициент передачи α₀ определяется как

где γ₀ - коэффициент инжекции; β₀ - коэффициент переноса; , U _КБ – напряжение между коллектором и базой; I _к – ток коллектора; I _э – ток эмиттера; I _pк и I _nк– дырочный и электронный токи коллектора, соответственно; I _pэ и I _nэ – дырочный и электронный токи эмиттера, соответственно.

При U _КБ < U _пробоя, M _к = 1, т.к. при малом уровне инжекции дырок в базу транзистора эмиттерный ток не управляет электронной составляющей тока через коллектор. Если коллекторное напряжение достаточно близко к напряжению лавинного пробоя, то M _к = коэффициенту лавинного умножения.

Таким образом, можно считать, что α = γ×β, тогда основное значение в зависимости α(ω) имеет зависимость β(ω), т.к.γ ≈ 1 и не изменяется с частотой в диапазоне до нескольких МГц. Для определения частотной зависимости β нужно решить уравнение непрерывности при наличии постоянных и переменных составляющих в эмиттерном токе и напряжении, , . Уравнение непрерывности

где p – концентрация дырок, D_p – коэффициент диффузии дырок, τ_p – время жизни дырок.

Решение уравнения (4) дает

где L_p – длина диффузии дырок, W – ширина базы биполярного транзистора.

В области низких частот (ωτ _p << 1) . При работе на высокой частоте усиление по току становится комплексной величиной, зависящей от частоты:

Модуль α:

Граничная частота, при которой модуль α уменьшается в √2 раз, находится из условия:

Откуда

где .

Более точное решение дает

где G (α₀) = 2,43 для случая α₀ ≈ 1.

Тогда

Модуль коэффициента передачи

Сдвиг по фазе определяется из условия

При значении частоты входного сигнала, равной ω_α, |α(ω_α)| = 0,71; φ_α = 60°. Амплитудо-частотная и фазо-частотная характеристики строятся обычно в нормированных координатах (рис. 3). Можно заметить, что они похожи на характеристики RC – цепи. Амплитудная кривая RC – цепи весьма точно воспроизводит ход теоретической амплитудной кривой. Фазовая кривая такой цепи дает существенные отклонения, особенно в области частот выше предельной.

Рис. 3. Зависимость нормированного коэффициента передачи и угла фазового сдвига φ_α от частоты входного сигнала ω. Сплошная линия – точное решение, пунктир – приближение RC- цепи.

Из выражения (9) следует, что предельную частоту усиления транзистора можно увеличивать за счет уменьшения толщины базы. Также ω_α можно повысить за счет создания в базе транзистора встроенного электрического поля, вектор напряженности которого должен быть направлен от эмиттера к коллектору. Предельные частоты дрейфовых транзисторов примерно в 10 раз превосходят значение этого параметра для транзисторов с однородным распределением примесей в базовой области. В настоящее время дрейфовый транзистор является основным типом высокочастотного транзистора.

Поделиться:

Воспользуйтесь поиском по сайту: