Основы технической термодинамики

ОПД.Ф.02.06 ТЕПЛОТЕХНИКА

УЧЕБОЕ ПОСОБИЕ

Для решения задач по разделу «Техническая термодинамика»

Специальности:

 

050501 – Профессиональное обучение

140106- Энергообеспечение предприятий

110301- Механизация сельского хозяйства

190601- Автомобили и автомобильное хозяйство

110302- Автоматизация и электрификация сельского хозяйства

 

Уфа 2008

 

УДК 621.1

ББК 31.3

М54

 

Методические указание разработаны доцентом Д.Х. Миграновым и переработаны

ст. преподавателем Инсафуддиновым С.З.

 

Рекомендовано к печати кафедрой «Автотракторные двигатели и теплотехника» (протокол № 30 от «28» января 200 8 г.) и методической комиссией факультета механизации сельского хозяйства (протокол № 43 от «28» января 200 8 г.).

 

Рецензент: доцент, кандидат технических наук Катков А.А.

 

Ответственный за выпуск: профессор Баширов Р.М.

 

 

ФГОУ ВПО «Башкирский ГАУ»,

кафедра «Автотракторные двигатели и теплотехника»

ВВЕДЕНИЕ

Настоящее методическое пособие предназначено для проведения практических занятий по курсу «Техническая термодинамика» со студентами факультетов «Механизация сельского хозяйства», «Энергетический», «Пищевых технологий» и «Землеустройства и лесного хозяйства» очного и заочного обучения.

В пособие включены разделы и задачи, связанные с процессами протекающими в машинах и аппаратах сельскохозяйственного назначения. Часть задач носит общетехнический характер, как и теоретический курс, применительно и программе которого написана пособие.

Все разделы пособия начинаются с краткого изложения основных сведений из теории, даны необходимые расчетные уравнения. В каждом разделе приведены решения нескольких характерных и наиболее сложных задач.

В приложениях к пособию приведен справочный материал, необходимый для решения задач.

 

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ

 

Величина	Размерность
Наименование	Обозначение	Обозначение	Наименование
Длина	l	м	метр
Диаметр	d	м	метр
Радиус	R	м	метр
Масса	m	кг	килограмм
Время	t	с	секунда
Температура: - термодинамическая - международная практическая	T t	К °С	кельвин градус Цельсия
Площадь	А	м²	метр квадр.
Объем	V	м³	метр кубич.
Объем удельный	υ	м³/кг	метр кубич. на кг
Плотность	ρ	кг/м³	килограм на кубич.метр
Количество теплоты	Q	Дж	джоуль
Теплота удельная	q	Дж/кг	Джоуль на кг
Сила	F	Н	Ньютон
Сила тяжести	P	Н	Ньютон
Вес удельный	γ	Н/м²	Ньютон на метр кубич.
Скорость: - линейная - угловая - звука	υ ω c	м/с рад/с м/с	метр в секунду радиан в сек. метр в секунду
Давление	p	Па	Паскаль
Мощность тепловая	Ф	Вт	Ватт
Подача насоса (компрессора, вентилятора): - массовая - объемная	mt Vt	кг/с м³/с	килограмм в сек. метр кубич в сек.
Постоянная газовая универсальная	R	Дж/(кмоль·К)	джоуль на киломоль-Кельвин
Постоянная газовая удельная	Ro	Дж/(кг·К)	Джоуль на килограм-Кельвин

Работа	W	Дж	Джоуль
Работа удельная	w	Дж/кг	Джоуль на килограмм
Расход -массовый -объемный	mt Vt	кг/с м³/с	килограммы в сек. метр кубич. в сек.
Градиент температуры	grad T	К/м	кельвин на метр
Теплопроводность (коэффициент теплопроводности)	λ	Вт/(мК)	Ватт на метр-Кельвин
Теплоемкость системы удельная при постоянном давлении при постоянном объеме	C C Cр сv	Дж/К Дж/(кг·К) Дж/(кг·К) Дж/(кг·К)	Джоуль на Кельвин   Джоуль на килограмм-Кельвин
Частота вращения	n	c-1	сек. в минус первой ст.
Ширина	b	м	метр
Энергия	E	Дж	Джоуль
Энергия внутренняя	H	Дж	Джоуль
Энергия внутренняя удельная	u	Дж/кг	Джоуль на килограмм
Энергия потенциальная	Ep	Дж	Джоуль
Энергия кинетическая	Ek	Дж	Джоуль
Энтальпия	H	Дж	Джоуль
Энтальпия удельная	h	Дж/кг	Джоуль на килограмм
Энтропия	S	Дж/К	Джоуль на Кельвин
Энтропия удельная	s	Дж/(кг·К)	Джоуль на килограмм-Кельвин
Частота колебаний	ν	c-1	сек.в минус первой степени
Теплота парообразования	r	Дж/кг	Джоуль на килограмм
Коэффициент теплоотдачи	α	Вт/(м2·К)	Ватт на квадратный метр -Кельвин
Коэффициент объемного расширения	β	К-1	Кельвин в минус первой степени
Температуропроводность	a	м2/с	квадратный метр на секунду
Коэффициент динамической вязкости	p	Па·с	Паскаль-секунда
Коэффициент кинематической вязкости	y	м2/с	квадратный метр на секунду
Степень черноты	ε
Коэффициент излучения	c	Вт/(м2·К4)	Ватт на квадратный метр - Кельвин в четвертой степени

ОСНОВЫ ТЕХНИЧЕСКОЙ ТЕРМОДИНАМИКИ

Параметры состояния термодинамической системы. Уравнение состояния рабочего тела.

В качестве рабочего тела в тепловых машинах используют газы и пары, обладающие способностью легко и быстро расширяться или сжиматься.

Физическое состояние рабочего тела определяется время основными параметрами состояния: температурой, давлением и удельным объемом.

Температура характеризует степень нагретости тела и измеряется в градусах. В настоящее время используются три температурные шкалы: абсолютная или термодинамическая шкала – Т, К, практическая международная шкала – t, °С, шкала Фаренгейта – t, °F.

Термодинамическая шкала установлена по температуре абсолютного нуля и тройной точки воды, равной 273,16 К, при которой могут существовать одновременно лед, вода и пар. Эту шкалу называют еще и абсолютной, так как температура измерения по ней не зависит от свойства теплоносителя. Цена деления шкалы в градусах Цельсия совпадает с ценой деления шкалы Кельвина (I К = I °С).

Численные значения температуры, определяемые по этим шкалам связаны соотношением

Т = t + 273,15, 1.1

По шкале Фаренгейта, применяемой в Англии и США, температура плавления льда 32 °F и температура кипения воды при нормальных физических условиях (Р₀ =I0I325 Па, Т₀=273,15 К) равна 212⁰ F следовательно

t°C= 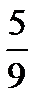(t°F­32), 1.2

Давление – это сила, действующая по нормам на единицу поверхности.

p = , 1.3

где F – сила, нормальная к поверхности и равномерно распределенная по поверхности площадью А.

Единицей давления в системе СИ является Паскаль (1 Па=1 Н/м²).

Очень часто в технике для практических измерений используют высоту столба жидкости. В основном применяется в качестве жидкости вода, спирт или ртуть. Полезно вспомнить, что при 0°C или 273,16 К.

I мм вод. ст.= 9,81 Па I мм рт. ст.= 133,3 Па

За параметр состояния в термодинамике принимают абсолютное давление. Абсолютное давление обычно, подчитывается по показаниям двух приборов.Если давление больше атмосферного (Р_б>Р_а ), то оно измеряется манометром и абсолютное давление равно:

Р_а=Р_б+Р_и, 1.4

где Р_б – атмосферное давление, измеренное барометром;

Р_и – показание манометра, измеряющего избыточное давление,

Если Р_б<Р_а , то Р_а=Р_б-Р_в, 1.5

где Р_в – показание вакуумметра, измеряющего разряжение.

Удельный объем тела:

, 1.6

где v - удельный объем, м³/кг;

V – полный объем, м³;

m – масса тела, кг.

Величина, обратная удельному объему называется плотностью вещества:

, 1.7

где - масса единицы, кг/м³.

Уравнение состояние тела устанавливают зависимость между параметрами состояния. Для идеального газа уравнение состояния выражается законом Клапейрона:

для 1 кг газа R₀T, 1.8

для m кг газа R₀T. 1.9

Для моля идеального газа уравнение предложено Менделеевым и имеет вид

МR₀Т=RT, 1.10

где V – объем моля газа, м³/кмоль;

R₀ – газовая постоянная, Дж/(кгК);

М – молекулярная масса, кг/кмоль;

R – универсальная газовая постоянная; её значение для всех газов 8314,3 Дж/(кмольК)

При нормальных физических условиях любой килограмм-моль газа занимает объем V=22,4 м³/кмоль. Поэтому для вычисления их удельного объема в м³/кг при этих условиях можно использовать зависимость

, 1.11

Газовая постоянная отдельного газа определяется по выражению

_,1.12

Объем газа V, находящегося при произвольных физических условиях (ρ и Т) может быть приведен к нормальным физическим условиям ( и ) по формуле

, 1.13

Значения удельной газовой постоянной, молекулярной массы и плотности при нормальных условиях для наиболее распространенных газов приведены в таблице

Таблица 1.1 Значение М, R₀ и ₀ при нормальных условиях некоторых газов.

Наименование газа	Химическое обозначение	Молекулярная масса М, кг/кмоль	Удельная газовая постоянная (R0, Дж/кгК)	Плотность при нормальных ф. у. ρ0, кг,м3
Воздух	­­-	28,96	287,0	1,293
Кислород	О2	32,00	259,68	1,429
Азот	N2	28,03	269,8	1,251
Аммиак	NH3	17,03	488,3	0,771
Аргон	Az	39,99	208,2	1,783
Атмосферный воздух	-	28,16	(295,3)	(1,257)
Водород	Н2	2,02	4124,0	0,090
Водяной пар	Н 2О	18,02	(461,0)	(0,804)
Гелий	На	4,00		0,179
Окись углерода	СО	28,01	296,8	1,260
Двуокись углерода	СО2	44,01	188,9	1,907
Сернистый газ	SО2	64,06	129,0	2,926
Метан	СН4	16,03	518,8	0,51
Этилен	С 2Н4	28,05	296,6	1,251
Коксиный газ	-	11,50	721,0	0,515

Примечание:

1. Атмосферный азот – углекислый газ, состоящий из азота воздуха вместе с двуокисью углерода и редкими газами, содержащимися в воздухе.

2. Приведение водяного пара к нормальному состоянию является условным.

Задачи.

Задача 1.1. Определить абсолютное давление в ресивире нересорной установки, если присоединенный к нему манометр подключает 0,3 Ма. Барометрическое давление по ртутному барометру составляет 240 мм рт.ст. при температуре ртути 20⁰С.

Решение: Для решения задачи необходимо перевести давление, измеренное по ртутному барометру в давление, выраженное в паскалях, и учесть температурную поправку.

Приведем показания барометра к 0⁰С по следующему соотношению

 

Р₀=Р(1-0,000172t),

где Р₀ - барометрическое давление, приведенное к 0⁰С;

Р - действительное давление при температуре воздуха 20⁰;

0,000172 – коэффициент объемного расширения ртути.

Р₀ = 740(1-172·10^-6·20)=737,45 мм. рт. ст.=98,3 кПа

Тогда абсолютное давление воздуха в ресивере

Р₀ = Р₀+Р_и=98,3+300=398,3 кПа.

 

Задача 1.2. Определить абсолютное давление в молокопроводе доильной установки, если вакуумметр, присоединенный к молокопроводу показывает разряжение 48 кПа, а барометрическое давление атмосферного воздуха 765 мм.рт.ст. при температуре 25⁰С.

Задача 1.3. Для предупреждения испарения ртути из трубки из ртутного манометра над уровнем ртути наливают слой воды. Определить абсолютное давление в сосуде, если высота столба ртути в манометре составляет 560 мм, а высота столба воды над ртутью равна 160 мм. Барометрическое давление равно 750 мм рт.ст.

Задача1.4. Разряжение на выходе дымохода парового котла измеряется тягомером с углом наклона трубки К горизонту 30⁰. Длина столба воды, отчитанная по шкале тягомера, равно 140 мм. Определить абсолютное давление газа в Мга, если показание барометра равно 750 мм рт.ст.

Задача1.5. В ресивере находится воздух массой 50 кг, плотностью 15 кг/м³. Определить емкость ресивера и удельный объем воздуха.

Задача1.6. Цилиндр, диаметром d=150 мм плотно закрыт подвешенном на пружине поршнем, условно невесомым и скользящим без трения. В цилиндре образован вакуум, составляющий 90% от барометрического давления ρ_б=0,1 МПа. Определить силу натяжения пружины, если поршень неподвижен.

Задача1.7. Для производства газосварочных работ привезли баллон с кислородом емкостью 40 л. Определить время расхода и массу израсходованного кислорода, если производительность горелки 1280 л/ч при абсолютном давлении 100 кПа и температуре 20⁰С, а избыточное давление в баллоне снизилось с 15 до 0,4 МПа.

Решение. Определяем абсолютное давление кислорода в баллоне до и после сварочных работ по формуле Р_а =Р_б+Р_и, так как параметром является только абсолютное давление.

Количество израсходованного кислорода определяется как разность кислорода, которая содержалась в баллоне до начала сварочных работ и после работ.

 

Δm=m₁-m₂=

За 1 час израсходовано

m_t= =1,68 кг/ч

 

Время расхода кислорода

 

t= 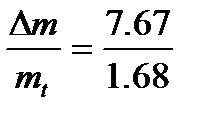=4,5 ч

 

Задача 1.8. Определить расход метана в газопроводе диаметром d=600 мм, если скорость истечения газа υ=15 м/с при абсолютном давлении 1,6 МПа и температуре 20⁰С.

Задача 1.9. Определить объемную подачу компрессора при температуре 25⁰С и барометрическом давлении 750 мм рт.ст., если при нормальных физических условиях она равна 3 м³/мин.

Задача 1.10. Определить площадь поперечного сечения воздуха вода дутьевого вентилятора, если каждую секунду в топку котла требуется подводить 10 кг воздуха плотностью 1,2 кг/м³. Скорость перемещения воздуха по воздуховоду принять равной 8 м/с.

 

СМЕСИ ИДЕАЛЬНЫХ ГАЗОВ

В практике очень часто приходится встречаться с газовыми смесями. Например, рабочее тело тепловых двигателей, компрессоров, других теплотехнических устройств, дымовые газы представляют собой смесь газов.

При рассмотрении газовых смесей исходят из того, что смесь состоит из идеальных химически не взаимодействующих между собой газов. При этом каждый газ, входящий в состав смеси, ведет себя так, как будто бы он один при данной температуре занимает весь объем смеси и оказывает на стенки сосуда свое давление, называется парциальным.

По закону Дальтона давление смеси р_см равно сумме парциальным давлений газов, входящих в состав смеси:

 

Р_см= Р₁+Р₂+····+Р_п= _j, 2.1.

 

Где Pι – прапорциональное давление компонента, входящего в смесь.

Состав смеси может выдан одним из следующих способов.

Массовый состав смеси

В абсолютных единицах массы

 

m_см=m₁+ m₂·····+ m_n= , 2.2

 

m₁, m₂, m_n –массы отдельных компонентов смеси

в относительных массовых долях

=q₁+ q₂ +···· + q_n=1; 2.3

 

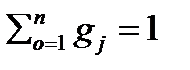, 2.4

где q_ι=m_ι/m_см – массовая доля отдельного компонента смеси.

Объемный состав смеси

V см=V₁+ V₂+·····+ V_n= 2.5

где V₁, V₂ и тд. – приведены объемы отдельных компонентов смеси, м³;

в относительных объемных долях

=1; 2.6

 

2.7

где - объемная доля отдельного компонента.

Задание состава смеси числом молей соответствует заданию состава смеси по объему, так как мольная доля компонента равна его объемной доле.

Между массовыми и объемными долями смеси существует следующая зависимость

, 2.8

Следовательно,

=qι ρ_см/ρ_ι 2.9

На основании следствия закона Авагадро

 

и

Соответственно

 

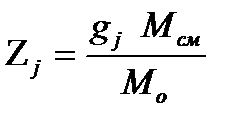, 2.10

Кажущая молекулярная масса газовой смеси

, 2.11

Газовая постоянная смеси может быть определена по составу смеси и газовым постоянным отдельных компонентов:

 

R_см= , 2.12

 

R_см= , 2.13

Или же по кажущейся молекулярной массе и универсальной газовой постоянной

 

R_см= , 2.14

 

Теплоемкость смеси газов определяется по ее составу. Массовая теплоемкость смеси газов

с_см=q₁с₁+ q₂с₂+····+q_nс_n= 2.15

 

где С₁, С₂····С_n – массовые теплоемкости отдельных компонентов

q₁, q₂····q_n – массовые доли отдельных компонентов.

Парциальное давление отдельного компонента.

 

Р_ι= 2.16

 

 

Задачи

Задача 2.1. Определить массовый состав сухого воздуха, его удельную газовую постоянную, кажущуюся относительную молекулярную массу и плотность при абсолютном давлении 110 кПа и температуре 20% кислорода и 79% азота.

Решение. Между массовыми и объемными составами газовой смеси существует зависимость

Кажущуюся молекулярную массу газовой смеси можно определить по формуле 2.11

 

м_см== ₀М₀+ _NМ_N=0,21·32+0,79·28=28,84

Тогда

g_N= ·М_N/М_см=0,79 ·28/28,84=0,767

g₀=1-g_N=1-0,767=0,233

Удельная газовая постоянная смеси определяется по формуле 2.14

R_см=8314,3/М_см=8314,3/28,84=288,3 кДж/(кг·K)

 

Плотность газовой смеси определяем из формулы

_см = == 1,182 кг/м³.

 

Задача 2.2. Смесь двух объемов водорода и одного объема кислорода называют гремучим газом. Определить кажушуюся молекулярную массу, газовую постоянную и массовый состав гремучего газа.

Задача 2.3. Смесь газов состоит из 1,0 м³ генераторного газа и 1,5 м³ воздуха, взятых при нормальных физических условиях. Определить газовую постоянную смеси газов и парциальные давления составляющих смеси. Плотность генераторного газа ρ₂ принять равной 1,2 кг/м³.

Задача 2.4. В цилиндр газового двигателя засасывается газовая смесь, состоящая из 20 массовых долей воздуха и одной доли коксового газа в смеси.

Задача 2.5. Анализ продуктов сгорания, произведенный с помощью газоанализатора показал их следующий объемный состав: СО₂=12,2%; О₂=7,1%; СО=0,4%; N₂=80,3%. Определить массовый состав входящих в смесь газов.

Задача 2.6. Определить объем смеси газов при абсолютном давлении 100 кПа и температуре 90⁰С, образовавшийся при смешивании 100 кг топочных газов с 50 кг воздуха. Массовый состав топочных газов _со=0,18; q_Но=0,08; q_о=0,02, и q_N=0,72.

 

 

ТЕПЛОЕМКОСТЬ ГАЗОВ

Теплоемкостью газа называют количество теплоты, необходимое для повышения его температуры на 1 К. Теплота, затраченная на повышение температуры единицы количества газа на 1 К называется удельной теплоемкостью. Принято удельную теплоемкость называть просто теплоемкостью.

В зависимости от выбранной количественной единицы различают теплоемкости: мольную С_m-кДж/(кмоль·К), массовую С – кДж/(кгК), и объемную С¹ – кДж/(м³К).

Так как в 1 м³ газа могут содержаться, в зависимости от параметров его состояния, разные количества газа, принято относить 1 м³ газа к нормальным условиям (Р₀= 101325 Па, Т₀=273,15 К).

Между теплоемкостями существует следующее соотношение

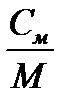С= 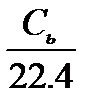; С^´= ; С= ; С^´=ρ₀·С, 3.1

где ρ₀ – плотность газа при нормальных условиях.

Теплоемкость газа зависит от его температуры. По этому признаку отличают истинную и среднюю теплоемкость.

Если q – удельное количество теплоты, сообщаемой единице количества вещества (или отнимаемый от него) при изменении температуры от t₁ до t₂, то величина

 

С=q/(t₂- t₁)=q/(Т₂- Т₁), 3.2

 

Представляет собой среднюю теплоемкость в пределах от t₂ до t₁.

Предел этого отношения, когда разность температур стремиться к нулю, называют истинной теплоемкостью. Аналитически последняя определяется как

3.3.

Теплоемкость зависит от вида процесса сообщаемая газу теплоты.

Для теплотехнических расчетов особое значение имеют теплоемкости газов при постоянном давлении и при постоянном объеме .

Между массовыми теплоемкостями и существуют соотношения:

где к- показатель адиабаты.

Постоянная теплоемкость политропного процесса с показателем n находитcя из выражения:

3.5

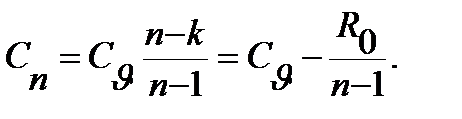
Для приближения расчетов при невысоких температурах теплоемкость можно считать постоянной.

Таблица 3.1 Приближенные значения мольных теплоемкостей при 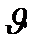= const, р- const

Газы	Теплоемкость,КДж/(кмольК)	Теплоемкость, КДж/(кмольК)	Показатель адиабаты,К
Одноатомные	20,93	12,56	1,67
Двухатомные	29,31	20,93	1,4
Трех- и многоатомные	37,68	29,31	1,2

При точных расчетах учитывают криволинейную зависимость теплоемкости от температуры и пользуются табличными значениями средних теплоемкостей в интервале от 0°С до t °С (Приложение1. ). Их отмечают сверху черточкой и указанием границ температур. Например: и т.д.

Менее точные расчеты, применяемые в технике получаются при использовании линейной зависимости теплоемкости от температуры. (Приложение 2)

Средняя теплоемкость в этом случае определяется в интервале температур от t1 до t2 по уравнению

3.6

где a и b величины, зависящие от физических свойств газа и постоянные для данного газа.

При пользовании таблицами значения истинных теплоемкостей, а также средних теплоемкостей в пределах от 0°С до t°С берутся не­посредственно из таблиц, причем в необходимых случаях проводится интерполирование.

Количество теплоты, которое необходимо затратить для нагре­вания или охлаждения рабочих тел определяются из соотношений:

а) для 1 кг: 3.7

для mкг 3.8

б) для 1 нормального кубического метра газа

3.9

для объема Vo вм^Э:

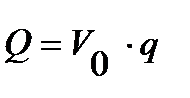3.10

В зависимости от условий, при "которых протекают нагревание (охлаждение) газа (V- const, p- const) в формулах 3.6...З.10 ставятся соответствующие значения теплоемкости.

Теплоемкость смеси идеальных газов:

массовая 3.11

объемная 3.12

Задачи.

Задача 3.1 Вычислить количество теплоты необходимой на нагревани е при постоянном давлении р=100 кПа,60 м³ воздуха от 10° до 500°С. Задачу решить в трех вариантах:

а) считая зависимость теплоемкости от температуры криволиней­ной;

б) пользуясь формулой линейной зависимости средней теплоемкос­ти воздуха от температуры;

в) полагая, что теплоемкость не зависит от температуры.

Решение. Количество теплоты, необходимое на нагревание воздуха, исходя из криволинейной зависимости теплоемкости от температуры определяем по следующей формуле, полученной на основании уравнений (3.7)и(3.8)

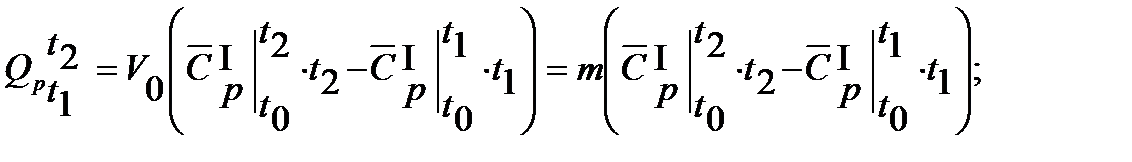
Если использовать при решении задачи объемные теплоемкости, то нужно найти объем воздуха при нормальных условиях (Р0=101325 Па и Т0=273,15 К). Можно определить массу воздуха и при­менить массовые теплоемкости.

Определяем массу воздуха по уравнению

Из приложения 1 выбираем средние изобарные массовые теплоем­кости от 0 до 10 и от 0 до 500°С.

В случае линейной зависимости теплоемкости от температуры формула для определения количества теплоты будет выглядеть

а при постоянной теплоемкости

Во второй случае использовали уравнения (.3.6), (3.8) и при­ложение 2, а в третьем-(3.1),. (3.8).и таблицу 3.1.

Задача 3.2. В котел-утилизатор поступают дымовые газы с температурой I200°С следующего объемного состава: С0₂=12%; О₂=6%,N=74%; пары воды H2O=8% при давлении 200 кПа. Определить количество подаваемой теплоты нагреваемой воде, если температура газов при выходе из котла 200°С, кпд котла – 70% и расход дымовых газов 10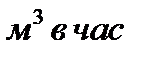

Решение. Определяем количество теплоты, отведенной от дымовых газов по уравнению

где V_o - объём газовой смеси при нормальных условиях;

- объемные доли отдельных компонентов дымовых газов.

Из уравнения состояния для m кг идеального газа необходим объем дымовых газов при нормальных условиях

Среднюю теплоемкость газов, входящих в состав дымовых газов берем из приложения I

Задача 3.3. Вычислить количество теплоты, удаляемое из птичника с отсасываемым воздухом, если температура внутри помещения 16,а наружного - 0°С. Объемная подача вентилятора20 тыс. стандартных м³/ч.

Задача 3.4.В конденсатор холодильной установки с водяным охлаждением поcтупает газообразный аммиак давлением р =1,05 MПa и температурной 122°С, охлаждается до t=27°C. Объемный расход аммиака V t=0_,04 м³/с. Вода в конденсаторе нагревается на 6⁰С. Определить количество отведенной теплоты и массовый расход воды на охлахдение конденсатора. Зависимость теплоемкости от температуры не учитывать.

Задача 3.5. В баллоне объемом 60л находится кислород при давлении 5 МПа и температуре 20°С. Какое количество тепла подведено.

к кислороду, если его температура повысилась до 150°С

Какое давление установится при этом в сосуде? Зависимость теплоемкости от температуры. принять криволинейной.

Задача 3.6. В воздухоподогревателе котельного агрегата дутьевой воздух нагревается дымовыми газами, от 20 до 200°С. При этом температура, дымовых газов понижается от 350 до 160°С. Объемный состав дымовых газов: С0₂=12%; О₂=6%,N=74%, H2O=8% Определить соотношение расходов воздуха и дымовых газов. Зависимость теплоем­кости газов и воздух от температуры считать прямолинейной.

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: