Перевод вещественных чисел

Представление данных в памяти ЭВМ

Для представления информации в памяти ЭВМ (как числовой, так и не числовой) используется двоичный способ кодирования.

Элементарная ячейка памяти ЭВМ имеет длину 8 бит (байт). Каждый байт имеет свой номер (его называют адресом). Наибольшую последовательность бит, которую ЭВМ может обрабатывать как единое целое, называют машинным словом. Длина машинного слова зависит от разрядности процессора и может быть равной 16, 32, 64 битам и т.д.

Кодирование символов

Для кодирования символов достаточно одного байта. При этом можно представить 256 символов (с десятичными кодами от 0 до 255). Набор символов персональных ЭВМ, совместимых с IBM PC, чаще всего является расширением кода ASCII (American Standard Code for Information Interchange — стандартный американский код для обмена информацией). В настоящее время используются и двухбайтовые представления символов.

В некоторых случаях при представлении в памяти ЭВМ чисел используется смешанная двоично-десятичная система счисления, где для хранения каждого десятичного знака нужен полубайт (4 бита) и десятичные цифры от 0 до 9 представляются соответствующими двоичными числами от 0000 до 1001. Например, упакованный десятичный формат, предназначенный для хранения целых чисел с 18-ю значащими цифрами и занимающий в памяти 10 байт (старший из которых знаковый), использует именно этот вариант.

Другой способ представления целых чисел - дополнительный код. Диапазон значений величин зависит от количества бит памяти отведенных для их хранения. Например, величины типа Integer лежат в диапазоне от
-32768 (-2¹⁵) до 32677 (2¹⁵-1) и для их хранения отводится 2 байта: типа LongInt - в диапазоне от -2³¹ до 2³¹-1 и размещаются в 4 байтах: типа Word - в диапазоне от 0 до 65535 (2¹⁶-1) используется 2 байта и т.д.

Как видно из примеров, данные могут быть интерпретированы как числа со знаком, так и без знаков. В случае представления величины со знаком самый левый (старший) разряд указывает на положительное число, если содержит нуль, и на отрицательное, если - единицу.

Вообще, разряды нумеруются справа налево, начиная с нуля.

Ниже показана нумерация бит в двухбайтовом машинном слове.

Дополнительный код положительного числа совпадает с его прямым кодом. Прямой код целого числа может быть представлен следующим образом: число переводиться в двоичную систему счисления, а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число. Например, если число 37₍₁₀₎ = 100101₍₂₎ объявлено величиной типа Integer, то его прямым кодом будет 0000000000100101, а если величиной типа LongInt, то его прямой код будет 00000000000000000000000000100101. Для более компактной записи чаще используют шестнадцатеричный код. Полученные коды можно переписать соответственно как 0025₍₁₆₎ и 00000025₍₁₆₎.

Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:

1. записать прямой код модуля числа;

2. инвертировать его (заменить единицы нулями, нули - единицами);

3. прибавить к инверсионному коду единицу.

Например, запишем дополнительный код числа -37, интерпретируя его как величину типа LongInt:

1. прямой код числа 37 есть 000000000000000000000000000100101

2. инверсный код 11111111111111111111111111011010

3. дополнительный код 11111111111111111111111111011011 или FFFFFFDB₍₁₆₎

При получении по дополнительному коду числа, прежде всего, необходимо определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему исчисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:

1. вычесть из кода 1;

2. инвертировать код;

3. перевести в десятичную систему счисления. Полученное число записать со знаком минус.

Примеры. Запишем числа, соответствующие дополнительным кодам:

a. 0000000000010111.

Поскольку в старшем разряде записан нуль, то результат будет положительным. Это код числа 23.

b. 1111111111000000.

Здесь записан код отрицательного числа, исполняем алгоритм:

1. 1111111111000000₍₂₎ - 1₍₂₎ = 1111111110111111₍₂₎;

2. 0000000001000000;

3. 1000000₍₂₎ = 64₍₁₀₎

Ответ: -64

Самостоятельно:

1) 1101100010-111=1101011011

2) 1101010000-111=1101001001

3) 100001-1011=10110

4) 1011-100001 (в 8 бит представление)= 11101010

a. 100001-1011=10110

b. Инвертируем: 10110 -> 01001

c. Прибавляем единицу: 01001+1=01010

d. Добавляем единицы СЛЕВА до 8 бит: 11101010

 

Почему отрицательные числа представляются в дополнительном коде? Дело в том, что в этом случае операция вычитания двух чисел сводится к сложению с дополнительным кодом вычитаемого, и процессору достаточно уметь лишь складывать числа. В самом деле:

А - В = А + (-В).

Проверим, действительно ли в ячейке памяти получится О в результате сложения числа 5628 с числом -5628 в форме дополнительного кода.

00000000 00000000 00010101 11111100 + 11111111 11111111 11101010 000000100 =

1 00000000 00000000 00000000 00000000

Что и требовалось доказать! Единица в старшем разряде, получаемая при сложении, выходит за границу разрядной сетки машинного слова и исчезает.

Двоичное 32-разрядное число 2₃₁ является «отрицательным самому себе». Получим его дополнительный код:

Определим по этим правилам внутреннее представление числа -5628₁₀ в 32-разрядной ячейке.

1.

2.

3.

Полученный код используется для представления значения

-2³¹ = -2147483648.

Следовательно, диапазон представления целых чисел в 32-разрядном машинном слове:

-2³¹ <= Х <= 2³¹-1,

или

-2147483648 <= Х <= 2147483647.

В общем случае для N-разрядного машинного слова этот диапазон такой:

-2^N-1 <= X <= 2^N-1-1.

В современных компьютерах часто используется 16- разрядное представление целых чисел. В этом случае их диапазон следующий:

-2¹⁵ <= Х <= 2¹⁵-1,

или

-32768 <= Х <= 32767.

Выход результатов вычислений за границы допустимого диапазона называется переполнением.

Переполнение при вычислениях с фиксированной точкой не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.

 

Вещественные числа. Числовые величины, которые могут принимать любые значения (целые и дробные) называются вещественными числами. В математике также используется термин «действительные числа». Решение большинства математических задач сводится к вычислениям с веществен-ными числами.

Перевод вещественных чисел

Перевод дробного числа из двоичной системы счисления в десятичную производится по следующей схеме:

101101,101₂ = 1·2 ⁵+ 0·2 ⁴+ 1·2 ³+ 1·2 ²+ 0·2 ¹+ 1·2 ⁰+ 1·2 ^-1+ 0·2 ^-2+ 1·2 ^-3= 45,625

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

1. Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

2. Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

3. В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

4. Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0. 232

.232 • 2 = 0. 464

.464 • 2 = 0. 928

.928 • 2 = 1. 856

.856 • 2 = 1. 712

.712 • 2 = 1. 424

.424 • 2 = 0. 848

.848 • 2 = 1. 696

.696 • 2 = 1. 392

.784 • 2 = 0. 784

И т.д.

Получим: 206₁₀=11001110,0001110110₂

Как же такие числа представляются в памяти компьютера?

Вещественные числа в памяти компьютера представляются в форме с плавающей точкой.

Любое действительное число можно записать в стандартном виде M*10^p, где 1 ≤ M < 10, р- целое число. Например, 120100000 = 1,201*10⁸. Поскольку каждая позиция десятичного числа отличается от соседней на степень числа 10, умножение на 10 эквивалентно сдвигу десятичной запятой на 1 позицию вправо. Аналогично деление на 10 сдвигает десятичную запятую на позицию влево. Поэтому приведенный выше пример можно продолжить: 120100000 = 1,201*10⁸ = 0,1201*10⁹ = 12,01*10⁷... Десятичная запятая плавает в числе и больше не помечает абсолютное место между целой и дробной частями.

В приведённой выше записи М называют мантиссой числа, а р - его порядком. Порядок указывает, на какое количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка».

Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа в форме с плавающей точкой.

Для того чтобы сохранить максимальную точность, вычислительные машины почти всегда хранят мантиссу в нормализованном виде, что означает, что мантисса в данном случае есть число, лежащее между 1₍₁₀₎ и 2₍₁₀₎ (1 ≤ М < 2).

Основные системы счисления здесь, как уже отмечалось выше, двоичные. Способ хранения мантиссы с плавающей точкой подразумевает, что двоичная запятая находится на фиксированном месте. Фактически подразумевается, что двоичная запятая следует после первой двоичной цифры, т.е. нормализация мантиссы делает единичным первый бит, помещая тем самым значение между единицей и двойкой. Место, отводимое для числа с плавающей точкой, делится на два поля. Одно поле содержит знак и значение мантиссы, а другое содержит знак и значение порядка.

Пусть в памяти компьютера вещественное число представляется в форме с плавающей точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы. Вот как эта информация располагается в ячейке:

± машинный порядок

М А

Н Т И С

С А

1-й байт 2-й байт 3-й байт 4-й байт

 

В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы.

Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. В десятичной системе это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка. В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие:

Машинный порядок					...			...
Математический порядок	-64	-63	-62	-61	...			...

Если обозначить машинный порядок Мр, а математический — р, то связь между ними выразится такой формулой:

Мр = р + 64.

или

Мр = р + 2⁶.

Внимание! Под порядок отводится 7 бит. Из них один - это 0 по середине между отрицательными и положительными. Остается 6. Поэтому смещение 2⁶=64.

Итак, машинный порядок смещен относительно математического на 64 единицы и имеет только положительные значения. При выполнении вычислений с плавающей точкой процессор это смещение учитывает.

Полученная формула записана в десятичной системе. Поскольку 64₁₀=40₁₆ (проверьте!), то в шестнадцатеричной системе формула примет вид:

Мр₁₆ = р₁₆ + 40₁₆

И, наконец, в двоичной системе:

Мр₂ = р₂+100 0000₂

Алгоритм 1. для получения представления действительного числа в памяти ЭВМ:

1. перевести модуль данного числа в двоичную систему счисления;

2. нормализовать двоичное число, т.е. записать в виде М*2^p, где М - мантисса (ее целая часть равна 1₍₂₎) и р - порядок, записанный в десятичной системе счисления;

3. перевести порядок в двоичную систему и прибавить к порядку смещение в двоичной системе;

4. учитывая знак заданного числа (0 - положительное; 1 - отрицательное), выписать его представление в памяти ЭВМ.

 

Пример: Записать внутреннее представление числа 25,324 в форме с плавающей точкой.

1. Переведем его в двоичную систему счисления с 24 значащими цифрами.

25,324₁₀= 11001,0101001011110001101₂

2. Запишем в форме нормализованного двоичного числа с плавающей точкой:

0,110010101001011110001101*10¹⁰¹

Здесь мантисса, основание системы счисления (2₁₀=10₂) и порядок (5₁₀=101₂)записаны в двоичной системе.

3. Вычислим машинный порядок.

Мр₂ = 101 + 100 0000 = 100 0101

4. Запишем представление числа в ячейке памяти.

Это и есть искомый результат. Его можно переписать в более компактной шестнадцатеричной форме:

CA

8D

Для того, чтобы получить внутреннее представление отрицательного числа -25,324,достаточно в полученном выше коде заменить в разряде знака числа 0 на 1.

Получим:

А в шестнадцатеричной форме:

C5

CA

8D

Никакого инвертирования, как для отрицательных чисел с фиксированной точкой, здесь не происходит.

Персональный компьютер IBM PC с математическим сопроцессором 8087 позволяет работать со следующими действительными типами (диапазон значений указан по абсолютной величине):

Тип	Диапазон	Мантисса	Байты
Real	2,9*10-39..1,7*1038	11-12
Single	1,5*10-45..3,4*1038	7-8
Double	5,0*10-324..1,7*10308	15-16
Extended	3,4*10-4932..1,1*104932	19-20

Покажем преобразование действительного числа для представления его в памяти ЭВМ на примере величины типа Double.

Как видно из таблицы, величина этого типа занимает в памяти 8 байт. На рисунке показано, как здесь представлены поля мантиссы и порядка:

	S	Смещенный порядок	Мантисса

Можно заметить, что старший бит, отведенный под мантиссу, имеет номер 51, т.е. мантисса занимает младшие 52 бита. Черта указывает здесь на положение двоичной запятой. Перед запятой должен стоять бит целой части мантиссы, но поскольку она всегда равна единице, здесь данный бит не требуется и соответствующий разряд отсутствует в памяти (но он подразумевается). Значение порядка храниться здесь не как целое число, представленное в дополнительном коде. Для упрощения вычислений и сравнения действительных чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к настоящему значению порядка, перед записью его в память, прибавляется смещение. Смещение выбирается так, чтобы минимальному значению порядка соответствовал нуль. Например, для типа Double порядок занимает 11 бит, поэтому смещение равно 2¹⁰=1023₍₁₀₎ = 1111111111₍₂₎ и значения имеют диапазон от 2^-1023 до 2^1023. Наконец, бит с номером 63 указывает на знак числа.

Алгоритм 2. для получения представления действительного числа в памяти ЭВМ:

5. перевести модуль данного числа в двоичную систему счисления;

6. нормализовать двоичное число, т.е. записать в виде М*2^p, где М - мантисса (ее целая часть равна 1₍₂₎) и р - порядок, записанный в десятичной системе счисления;

7. прибавить к порядку смещение и перевести смещенный порядок в двоичную систему счисления;

8. учитывая знак заданного числа (0 - положительное; 1 - отрицательное), выписать его представление в памяти ЭВМ.

Пример: Запишем код числа -312,3125.

1. Двоичная запись модуля этого числа имеет вид 100111000,0101.

2. Имеем 100111000,0101 = 1,001110000101*2⁸.

3. Получаем смещенный порядок 8 + 1023 = 1031. Далее имеем 1031₍₁₀₎ = 10000000111₍₂₎.

4. Окончательно

Очевидно, что более компактнополученный код стоит записать следующим образом: C073850000000000(16).

 

Пример: Обратный переход от кода действительного числа к самому числу.

Пусть дан код 3FEC600000000000₍₁₆₎ или

1. Прежде всего, замечаем, что это код положительного числа, поскольку в разряде с номером 63 записан нуль, Получим порядок этого числа. 01111111110₍₂₎ = 1022₍₁₀₎. 1022 - 1023 = -1.

2. Число имеет вид 1,1100011*2^-1 или 0,11100011.

3. Переводом в десятичную систему счисления получаем 0,88671875.

 

Рассмотрим, наконец, вопрос о диапазоне чисел, представимых в форме с плавающей точкой. Очевидно, положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю: Rmax = |Rmin|. Наименьшее по абсолютной величине число равно нулю. Чему же равно Rmax? Это число с самой большой мантиссой и самым большим порядком:

0,111111111111111111111111*10₂^1111111

Если перевести в десятичную систему, то получится

Rmax = (1 - 2^-24) * 2⁶⁴ = 10¹⁹

Очевидно, что диапазон вещественных чисел значительно шире диапазона целых чисел. Если в результате вычислений получается число по модулю большее, чем Rmax, то происходит прерывание работы процессора. Такая ситуация называется переполнением при вычислениях с плавающей точкой. Наименьшее по модулю ненулевое значение равно:

(1/2)*2^-64=2^-66.

Любые значения, меньшие данного по абсолютной величине, воспринимаются процессором как нулевые.

Как известно из математики, множество действительных чисел бесконечно и непрерывно. Множество же вещественных чисел, представимых в памяти ЭВМ в форме с плавающей точкой, является ограниченным и дискретным. Каждое следующее значение получается прибавлением к мантиссе предыдущего единицы в последнем (24-м) разряде. Количество вещественных чисел, точно представимых в памяти машины, вычисляется по формуле:

N = 2^t (U - L+ 1) + 1.

Здесь t — количество двоичных разрядов мантиссы; U — максимальное значение математического порядка; L — минимальное значение порядка. Для рассмотренного нами варианта (t = 24, U = 63, L = -64) получается:

N = 2 146 683 548.

Все же остальные числа, не попадающие в это множество, но находящиеся в диапазоне допустимых значений, представляются в памяти приближенно (мантисса обрезается на 24-м разряде). А поскольку числа имеют погрешности, то и результаты вычислений с этими числами также будут содержать погрешность. Из сказанного следует вывод: вычисления с вещественными числами в компьютере выполняются приближенно.

Вопросы и задания

1. Что такое форма с фиксированной точкой? Для представления каких чисел в компьютере она используется?

2. Как в форме с фиксированной точкой представляются целые положительные и отрицательные числа?

Работа с С++

Пример 1. Запуск программы в Dev-C++

system("pause");- пауза в программе до нажатия любой клавиши;

Пример:

#include <stdio.h> (для функции printf)

#include <stdlib.h> (для функции system)

main()

{

int x=2;

printf("x=%d ",x);

system("pause");

}

 

 

Пример 2. Вывод размеров типов и их максимальных значений.

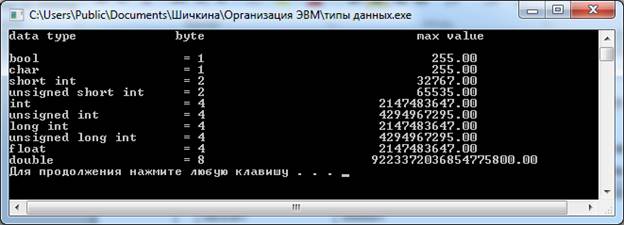
По программе:

#include <stdio.h>

#include <math.h>

#include <stdlib.h>

main()

{

int x=2;

printf("data type byte max value ");

printf("bool = %d %14.2f ", sizeof(bool), (pow(2,sizeof(bool) * 8.0) - 1));

printf("char = %d %14.2f ", sizeof(char), (pow(2,sizeof(char) * 8.0) - 1));

printf("short int = %d %14.2f ", sizeof(short int), (pow(2,sizeof(short int) * 8.0-1) - 1));

printf("unsigned short int = %d %14.2f ", sizeof(unsigned short int), (pow(2,sizeof(unsigned short int) * 8.0) - 1));

printf("int = %d %14.2f ", sizeof(int), (pow(2,sizeof(int) * 8.0-1) - 1));

printf("unsigned int = %d %14.2f ", sizeof(unsigned int), (pow(2,sizeof(unsigned int) * 8.0) - 1));

printf("long int = %d %14.2f ", sizeof(long int), (pow(2,sizeof(long int) * 8.0-1) - 1));

printf("unsigned long int = %d %14.2f ", sizeof(unsigned long int), (pow(2,sizeof(unsigned long int) * 8.0) - 1));

printf("float = %d %14.2f ", sizeof(float), (pow(2,sizeof(float) * 8.0-1) - 1));

printf("double = %d %14.2f ", sizeof(double), (pow(2,sizeof(double) * 8.0-1) - 1));

system("pause");

return 0;

printf("x=%d, Size=%d (byte) ",x,sizeof(5));

for(int i=sizeof(x)*8-1; i>=0; --i){

printf("%d", x&(1<<i)?1:0);}

printf(" ",x);

system("pause");

}

 

Функция sizeof(x) – возвращает объем занимаемой памяти в байтах.

Пример: sizeof(int); sizeof(x); sizeof(A) где А – массив; sizeof(23)

 

Расхождение с интернет:

Максимальное значение некоторого типа данных вычисляется по такой формуле:

· для типов данных с отрицательными и положительными числами

max_val_type = 2^(b * 8 - 1) - 1;

где, b - количество байт выделяемое в памяти под переменную с таким типом данных Умножаем на 8, так как в одном байте 8 бит. Вычитаем 1 в скобочках, так как диапазон чисел надо разделить надвое для положительных и отрицательных значений. Вычитаем 1 в конце, так как диапазон чисел начинается с нуля.

· для типов данных с приставкой unsigned (для типов данных только с положительными числами)

max_val_type = 2^(b * 8) - 1;

Пояснения к формуле аналогичные, только в скобочка не вычитается единица

Таблица 1 — Типы данных С++

Тип	байт	Диапазон принимаемых значений
целочисленный (логический) тип данных
bool		0 / 255
целочисленный (символьный) тип данных
char		0 / 255
целочисленные типы данных
short int		-32 768 / 32 767
unsigned short int		0 / 65 535
int		-2 147 483 648 / 2 147 483 647
unsigned int		0 / 4 294 967 295
long int		-2 147 483 648 / 2 147 483 647
unsigned long int		0 / 4 294 967 295
типы данных с плавающей точкой
float		-2 147 483 648.0 / 2 147 483 647.0
long float		-9 223 372 036 854 775 808.0 / 9 223 372 036 854 775 807.0
double		-9 223 372 036 854 775 808.0 / 9 223 372 036 854 775 807.0

 

 

Пример 3. Печать десятичного числа в двоичном виде:

#include <stdio.h>

#include <math.h>

#include <stdlib.h>

main()

{

int x=2;

printf("x=%d, Size=%d (byte) ",x,sizeof(int));

for(int i=sizeof(x)*8-1; i>=0; --i){

printf("%d", x&(1<<i)?1:0);}

printf(" ",x);

system("pause");

}

 

Побитовые операторы

Побитовые операции рассматривают операнды как упорядоченные наборы битов, каждый бит может иметь одно из двух значений – 0 или 1. Такие операции позволяют программисту манипулировать значениями отдельных битов. Объект, содержащий набор битов, иногда называют битовым вектором. Он позволяет компактно хранить набор флагов – переменных, принимающих значение “да” “нет”. Например, компиляторы зачастую помещают в битовые векторы спецификаторы типов, такие, как const и volatile. Библиотека iostream использует эти векторы для хранения состояния формата вывода.

При работе с битовыми векторами также можно применять подход, заимствованный из С, – использовать для представления такого вектора объект встроенного целого типа, обычно unsigned int, или класс bitset стандартной библиотеки С++. Этот класс инкапсулирует семантику вектора, предоставляя операции для манипулирования отдельными битами. Кроме того, он позволяет ответить на вопросы типа: есть ли “взведенные” биты (со значением 1) в векторе? Сколько битов “взведено”?

В общем случае предпочтительнее пользоваться классом bitset, однако, понимание работы с битовыми векторами на уровне встроенных типов данных очень полезно. В этом разделе мы рассмотрим применение встроенных типов для представления битовых векторов, а в следующем – класс bitset.

При использовании встроенных типов для представления битовых векторов можно пользоваться как знаковыми, так и беззнаковыми целыми типами, но мы настоятельно советуем пользоваться беззнаковыми: поведение побитовых операторов со знаковыми типами может различаться в разных реализациях компиляторов.

Таблица 2. Побитовые операторы

Символ операции	Значение	Использование
~	Побитовое НЕ	~expr
<<	Сдвиг влево	expr1<<expr2
>>	Сдвиг вправо	expr1>>expr2
&	Побитовое И	expr1 & expr2
^	Побитовое Исключающее ИЛИ	expr1 ^ expr2
|	Побитовое ИЛИ	expr1 | expr2
&=	Побитовое И с присваиванием	expr1 &= expr2
^=	Побитовое ИсклИЛИ с присваиванием	expr1 ^= expr2
|=	Побитовое ИЛИ с присваиванием	expr1 |= expr2
<<=	Сдвиг влево с присваиванием	expr1 <<= expr2
>>=	Сдвиг вправо с присваиванием	expr1 >>= expr2

Побитовое отрицание

Побитовое НЕ (~) меняет значение каждого бита операнда. Бит, установленный в 1, меняет значение на 0 и наоборот.

Битовые сдвиги

При сдвиге значения битов копируются в соседние по направлению сдвига. Различают несколько видов сдвигов — логический, арифметический и циклический, в зависимости от обработки крайних битов.

Также различают сдвиг влево (в направлении от младшего бита к старшему) и вправо (в направлении от старшего бита к младшему).

Операторы сдвига (<<, >>) сдвигают биты в левом операнде на указанное правым операндом количество позиций. “Выталкиваемые наружу” биты пропадают, освобождающиеся биты (справа для сдвига влево, слева для сдвига вправо) заполняются нулями. Однако нужно иметь в виду, что для сдвига вправо заполнение левых битов нулями гарантируется только для беззнакового операнда, для знакового в некоторых реализациях возможно заполнение значением знакового (самого левого) бита.

Логический сдвиг

При логическом сдвиге значение последнего бита по направлению сдвига теряется (копируясь в бит переноса), а первый приобретает нулевое значение.

12	Поделиться:

Воспользуйтесь поиском по сайту: