Задания для самостоятельного решения

Основные понятия.

Мощность алфавита – это количество различных символов, которые можно получить с помощью кодовой цепочки, состоящей из I битов. Биты для измерения информации используются тогда, когда каждый элемент цепочки может принимать 2 устойчивых состояния.

N =2 ^I (1)

Информационная емкость символа, т.е. количество информации, которое несет один знак, зависит от количества символов в алфавите:

I = ­ log₂ N (2)

Количество информации, которое содержит сообщение V, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак I, умноженному на количество знаков в сообщении n.

V = I×n (3)

Пример 1: Каждый символ закодирован одним байтом. Оцените информационный объем (в битах) следующего предложения в этой кодировке:

В одном килограмме 1000 грамм.

Решение.

Количество символов в фразе n =30. Каждый символ равен 1 байту, следовательно, фраза будет занимать 30 байт информации, что составит:

I = 30 · 8 =240 бит информации.

Пример 2: Пользователь компьютера, хорошо владеющий навыками ввода ин­формации с клавиатуры, может вводить в минуту 100 знаков. Мощ­ность алфавита, используемого в компьютере, равна 256. Какое ко­личество информации в байтах может ввести пользователь в компьютер за 12 минут?

Решение.

Найдем количество символов n, которые пользователь может ввести за 12 минут: n =12 × 100=1200 символов. Информационная емкость символа при мощности N =256 составит: I = ­ log₂ 256=8 бит=1 байт на 1 символ. Следовательно, количество информации,которое может ввести пользователь V= 1байт × 1200=9600 =1200 байт.

Информация может рассматриваться как уменьшение неопределенности состояния системы, а количество информации определяется как разность энтропий:

I (X)= H (X)- H '(X). (4)

Для случая, когда система имеет n состояний, и все они равновероятны, используется формула Хартли:

I = ­ log₂ n. (5)

Пример 3: Световое табло состоит из лампочек, каждая из которых может находиться в двух состояниях ("включено" или "выключено"). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

Решение.

Количество сигналов n =50, лампочки могут находиться в 2-х состояниях, следовательно, необходимо найти показатель степени (целое число), в которое необходимо возвести 2, чтобы получилось число большее 50, и наиболее близко к нему расположено: I = log₂ 50» 6; минимально потребуется 6 лампочек, т.к. с помощью 5-ти лампочек можно закодировать лишь 32 сигнала.

Из формул (4) и (5) можно получить:

I= log₂ n ₁–log₂ n ₂=log₂ n ₁/ n ₂. (6)

Пример 4: В стопке дисков находятся 8 дисков с прикладными программами, 6 дисков с обучающими программами и 10 игр. Какое количество информации получено, если известно, что случайно извлеченный диск – это диск с обучающей программой?

Решение.

Первоначально количество исходов извлечения диска n ₁=8+6+10=24, после получения сообщения n ₂=6, можно применить формулу 6:

I = log₂ 24 – log₂ 6 = log₂ 24/6 = log₂4 =2 бита информации.

Под собственной информацией будем понимать информацию, содержащуюся в данном конкретном сообщении, которое дает получателю информацию о возможности существования конкретного состояния системы. Тогда количество собственной информации, содержащееся в сообщении S_i, определяется как:

I (S_i)= –log ₂ P (S_i) (7)

Собственная информация имеет следующие свойства:

1. Неотрицательна.

2. Чем меньше вероятность возникновения сообщения, тем больше информации оно содержит.

3. Информация равна 0, если вероятность возникновения сообщения равна 1.

4. Количество собственной информации нескольких независимых сообщений равно их сумме.

I (X_i, Y_i)= –log ₂ P (X_i) – log ₂ P (Y_i)= I (X_i)+ I (Y_i).

Пример 5: У скупого рыцаря в сундуке золотые, серебряные и медные монеты. Каждый вечер он извлекает из сундука одну из лежащих в нем 96 монет, любуется ею, и кладет обратно в сундук. Количество информации, содержащееся в сообщении «Из сундука извлечена серебряная монета», равно 4 бита. Информационный объем сообщения «Из сундука извлечена золотая монета» равен 5 бит. Сколько медных монет было в сундуке.

Решение.

Обозначим сообщение «Из сундука извлечена золотая монета» за S ₁; а сообщение «Из сундука извлечена серебряная монета» за S ₂; k ₁ – количество золотых монет; k ₂ – количество серебряных монет; k ₃ – количество медных монет; общее количество монет k = k ₁+ k ₂ + k ₃ = 96.

По формуле (7) I (S_i) = -log₂ P (S_i) = log₂

и соотношения можно найти:

I (S ₁) = 5 бит, ;

– в сундуке 3 золотых монеты

 

I (S ₂) = 4 бита, ;

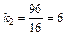– в сундуке 6 серебряных монет

k ₃ = k – (k ₁+ k ₂) = 96 – (6+3) =87 – в сундуке 87 медных монет.

 

Теорема Шеннона. Если система X обладает дискретными состояниями, их количество равно n, а вероятность нахождения в каждом из состояний p (A ₁), p (A ₂),…, p (A_n), то энтропия система H (X) равна:

(8)

Свойства энтропии

1. H= 0 в двух случаях: Какая-либо из P (A_j) = 1, следовательно, все остальные P (A_i) = 0 (i ¹ j) или все P (A_i) = 0.

2. a и b независимые опыты: H(aÙb)=H(a)+H(b).

3. a и b зависимые опыты: H(aÙb)=H(a)+H_a(b), где

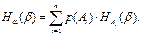
Пример 6: Имеются 2 ящика, в каждом по 12 шаров. В первом 3 белых, 3 черных и 6 красных. Во втором – каждого цвета по 4. Опыт состоит в извлечении по одному шару из каждого ящика. Найти энтропию извлечения.

Решение.

a – извлечение шара из I ящика; A ₁ – извлекли белый шар; A ₂ – извлекли черный шар; A ₃ – извлекли красный шар; A ₁ и A ₂ – события равновероятны: p (А ₁)= p (А ₂ )=3/12=1/4=0,25; p (А ₃ )=6/12=1/2.

H (a) = –0,25 log₂ 0,25–0,25 log₂ 0,25–0,5 log₂ 0,5 = 1,5 бит

a и b – независимые опыты. Вероятность извлечения шаров определенного цвета из II ящика – одинаковая, по формуле (5) при n = 3 H (b) =­ log₂ 3» 1,585 бита.

H(aÙb)=H(a)+H(b). H(aÙb) = 1,5+1,585=3,085 бита.

Пример 7: В ящике 2 белых, 4 черных и 6 красных шара. Из ящика извлекают последовательно 2 шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.

Решение.

Опыт a – извлекли I шар: А ₁ – шар белого цвета, А ₂ – шар черного цвета; А ₃ – шар красного цвета события равновероятны p (А ₁)= 1/6; p (А ₂)= 1/3; p (А ₃)=1/2, по теореме Шеннона при n =3:

H (a) = – p (А ₁) log₂ p (А ₁) – p (А ₂) log₂ p (А ₂) – p (А ₃) log₂ p (А ₃) = .

Опыт b – извлекли II шар возможны исходы: В₁ – шар белого цвета; В₂ – шар черного цвета; В_{3 _} – шар красного цвета.

,

аналогично, H_A2 (b)= 1,43; H_A3 (b)= 1,45

H_a (b) = p (А₁) H_A1 (b) + p (А ₂) H_A2 (b) + p (А ₃) H_A3 (b) =

= 0,17 ×1,32+0,33×1,43+0,5×1,45 = 0,22+0,47+0,73=1,42 бита.

Энтропия сложного опыта: H (aÙb)= H (a)+ H_a (b)= 1,46+1,42 = 2,88 бита.

 

Коэффициент содержательности С как мера семантической информации:

С = I_c / V (9)

Пример 8: Чему равен коэффициент содержательности информации, если из 100 страниц учебника студенту непонятно 20 страниц, а на 10 страницах находится информация, которая ему была уже известна?

Решение.

С=I_c / V, V = 100 страниц – общий объем учебника;

I_c = 100-20-10=70страниц семантической информации, которая для студента является новой и понятной, т.е. он может ее понять (интерпретировать).

Коэффициент содержательности информации учебника для этого студента составит: С= 70/100=0,7.

Количественная мера прагматической информации:

(10)

p_o – вероятность достижения цели до получения информации;

p₁ – вероятность достижения цели после получения информации.

Пример 9: Водитель автомобиля нарушил правила, случайный свидетель смог лишь вспомнить, что все цифры номера нечетные и разные. Какое количество прагматической информации получено от случайного свидетеля?

Решение.

, вероятность определения номера до получения информации от свидетеля;

, вероятность определения номера после получения информации, тогда по формуле (9):

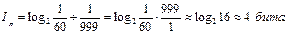
Задания для самостоятельного решения

Задание 1. Система оптического распознавания символов позволяет преобразо­вывать отсканированные изображения страниц документа в тексто­вый формат со скоростью 4 страницы в минуту и использует алфа­вит мощностью 65536 символов. Какое количество информации будет нести текстовый документ после 5 минут работы приложения, страницы которого содержат 40 строк по 50 символов?

Задание 2. Какова мощность алфавита, с помощью которого записано сообще­ние, содержащее 2048 символов, если его объем составляет 1/128 часть одного мегабайта?

Задание 3. При угадывании результата броска игральной кости задается вопрос «Выпало 3?». Какое количество информации содержит ответ?

Задание 4. Злой экзаменатор никогда не ставит пятерок по информатике. По причине своей зловредности он заранее определил количество отметок каждого вида и произвольно расставил их абитуриентам. Количество информации, содержащееся в сообщении «Абитуриент Иванов не провалился на экзамене», равно log ₂3 бит. Информационный объем сообщения «Абитуриент Сидоров получил тройку» равен двум битам. 22 абитуриента получили двойку или тройку. Сколько абитуриентов сдавали информатику?

Задание 5. В некоторой местности имеется две близкорасположенные деревни: А и В. Известно, что жители А всегда говорят правду, а жители В – всегда лгут. Известно также, что жители обеих деревень любят ходить друг к другу в гости, поэтому в каждой деревни можно встретить жителя соседней деревни. Путешественник, сбившись ночью с пути, оказался в одной из двух деревень и, заговорив с первым встречным, захотел выяснить, в какой деревне он находится и откуда его собеседник. Какое минимальное количество вопросов с бинарными ответами требуется задать путешественнику?

Вопросы для самоконтроля

1. Какова связь между понятиями «энтропия» и «информация»?

2. Почему для измерения энтропии выбрана логарифмическая функция?

3. Почему за основание логарифма выбрали 2?

4. Приведите примеры независимых опытов.

5. Приведите примеры зависимых опытов.

Индивидуальные задания

1. В спартакиаде участвуют 215 учеников. Какое минимальное количество бит необходимо, чтобы закодировать номер каждого ученика?

2. Случайным образом вынимается карточка из стопки в 32 карточки. Какое количество информации требуется, чтобы угадать, что это за карточки?

3. Приветствие от марсиан записано с помощью всех символов марсианского алфавита: ТЕВИРП!КИ! Сколько информации оно содержит?

4. Какое количество информации несет сообщение о том, что нужная вам тетрадь находится в одном из восьми ящиков стола?

5. Считая, что каждый символ кодируется 16-ю битами, оцените информационный объем следующей пушкинской фразы в кодировке Unicode: «Привычка свыше нам дана: Замена счастью она.»

6. Световое табло из лампочек, каждая из которых может находиться в двух состояниях («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 299 разных сигналов?

7. Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100%, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Каков информационный объем результатов наблюдений?

8. Азбука Морзе позволяет кодировать символы для радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее 5 и не более 6 сигналов (точек и тире)?

9. Какое наименьшее число символов должно быть в алфавите, чтобы при помощи всевозмозможных трехбуквенных слов, состоящих из символов данного алфавита, можно было передать не менее 12 различных сообщений?

10. По выигранному гранту в школу поступила партия ноутбуков, принтеров и сканеров. Из них 27 ноутбуков. Для проверки качества поступившей аппаратуры заместитель директора по хозяйственной части случайным образом выбирает одну из коробок. Информационный объем сообщения «Для проверки выбран не ноутбук» равен 4-log₂7 бит. Количество собственной информации, содержащееся в сообщении «Для проверки выбран не принтер», равно log₂3-1 бит. Сколько сканеров поступило в школу?

11. Сколько секунд потребуется модему, передающему информацию со скоростью 64 000 бит/с, чтобы передать 16-цветное растровое изображение размером 1200´800 пикселей при условии, что в одном байте закодировано максимально возможное число пикселей?

12. Метеорологическая станция ведет наблюдение за атмосферным давлением. Результатом одного измерения является целое число, принимающее значение от 720 до 780 мм ртутного столба, которое записывается при помощи минимально возможного количества бит. Станция сделала 120 измерений. Каков информационный объем в байтах результатов наблюдений?

 

Поделиться:

Воспользуйтесь поиском по сайту: