 |
Этапы экспертного прогнозирования.
|
|
|
|
ТЕМА 4 Этапы прогнозирования
Этапы прогнозирования на базе временных рядов.
Этапы экспертного прогнозирования.
4.1 Разработка прогнозов на базе временных рядов осуществляется по этапам:
1. Построение и сглаживание исходных данных.
2. Обоснование вида и расчет параметров функции, отражающей динамику прогнозируемого показателя.
3. Расчет прогнозных оценок на перспективу и проверка надежности полученных прогнозов.
На первом этапе выявляется характер изменения прогнозируемого показателя во времени. Для этого исходные данные наносят на плоскость, имеющую одинаковый масштаб по горизонтальной и вертикальной осям. При таком построении сводится к минимуму искажение зависимости прогнозируемого признака от времени и обеспечивается наглядность.
Однако не всегда с помощью графического построения можно определить устойчивую закономерность. В этом случае исходные данные подвергаются дополнительной обработке: сглаживание рядов или определение последовательных разностей.
Наиболее простым методом сглаживания временных рядов является метод скользящей средней. С помощью этого метода осуществляется замена фактических значений усредненными показателями.
Из полученных средних формируется новый динамический ряд, в котором в значительной степени устранено влияние случайных внешних факторов.
В зависимости от периода различают скользящие средние для нечетного и четного числа интервалов времени. Более простой расчет средних – использование нечетного числа интервалов времени. Для трех- и пятичленных средних расчет выполняется по следующим формулам:
 , t=2, 3, 4,..., (n-1); (1)
, t=2, 3, 4,..., (n-1); (1)
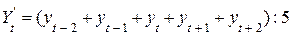 , t= 3, 4, 5,..., (n-2), (2)
, t= 3, 4, 5,..., (n-2), (2)
где  - скользящая средняя.
- скользящая средняя.
|
|
|
В том случае, когда имеется предположение, что зависимость анализируемого признака во времени характеризуется одним из многочленов:
 (3)
(3)

 ; (4)
; (4)

 ; (5)
; (5)

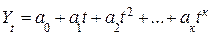 (6)
(6)
для выбора конкретного вида уравнения используется метод конечных разностей.
В основе этого метода лежит свойство полинома степени k обращать в нуль разности  и придавать одинаковые значения разностям
и придавать одинаковые значения разностям  .
.
Для расчета разностей n-го порядка применяются следующие формулы:
1-го порядка 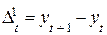 (t = 1, 2, 3,...n); (7)
(t = 1, 2, 3,...n); (7)
2-го порядка  ; (8)
; (8)
3-го порядка  . (9)
. (9)
Методы скользящих средних и конечных разностей упрощает выявление закономерностей изменения прогнозируемого показателя. Они позволяют наглядно представить динамику процесса, однако нельзя получение оценки рассматривать как безусловные доказательства для предвидения будущего.
Научно обоснованный прогноз требует предвидения глубокого качественного анализа причин, влияющих на признак, исследование тенденции его развития и взаимодействия с внешними факторами.
Найденная математическая зависимость прогнозирующей функции от фактора и представления в форме конкретного уравнения называемого трендом.
Для определения параметров тренда применяют различные методы, среди которых наибольшее распространение получил метод наименьших квадратов.
Применение метода наименьших квадратов позволяет устанавливать наличие связи между признаками временного ряда и определять константы и коэффициенты функции Yt = f (t). Во временных рядах в качестве независимой переменной выступает показатель времени – t.
Метод наименьших квадратов делает возможным найти такую функцию, отклонения которой от фактических значений динамического ряда (Yt) будут минимальными. Аналитически это выражается формулой:

 (10)
(10)
Подставив в уравнение (10) связи функции с фактором времени (t), получим следующее выражение:
 . (11)
. (11)
Приравняв частные производные выражения (11) нулю и после соответствующих преобразований, получим систему уравнений для линейного тренда:
|
|
|

 ;
;
 . (12)
. (12)
После подстановки в систему (12) имеющейся исходной информации (yt и t) рассчитывают параметры тренда «а» и «b». Значение «n» в парном нормальном уравнении системы означает длину исходного временного ряда.
Если характер изменения признака описывается полиномом 2-го и более высокого порядка, необходимо придерживаться следующего правила построения системы нормальных уравнений.
1. Записывается общий вид уравнения
yt= a+bt+ct  . (13)
. (13)
2. Выделяются искомые параметры:
а, b, c.
3. Умножается свободный член уравнения (13) «а» на общее число эллементов в динамическом ряду «n». Перед другими членами уравнения ставится знак суммирования -  .
.
 yt= na+b
yt= na+b  t+c
t+c  t
t  . (14)
. (14)
Если в уравнении (13) свободный член «а» отсутствует, действие третьего этапа не выполняется.
4. Умножаются все члены уравнения на t при втором искомом параметре «b». Перед всеми другими членами ставится знак суммирования -  .
.
 yt t= a
yt t= a  +b
+b  t
t  +c
+c  t
t 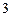 . (15)
. (15)
5. На последующих этапах умножение повторяется до тех пор, пока не будут использованы все сомножители, стоящие рядом с искомыми параметрами.
Общее количество нормальных уравнений должно соответствовать числу параметров, подлежащих определению.
Последнее (третье) уравнение в рассматриваемом случае имело бы следующий вид:
 yt t
yt t  = a
= a 
 +b
+b  t
t 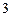 +c
+c  t
t  . (16)
. (16)
Рассчитав все суммы ( ), определяют константы уравнения (а, в, с,...,k).
), определяют константы уравнения (а, в, с,...,k).
В тех случаях когда, в качестве тренда используется гиперболическая, экспоненциальная, степенная, логистическая и некоторые другие функции, первоначально проводится линеризация кривой, позволяющая перейти от нелинейных связей к линейным (табл.2).
Таблица 2 - Линеризация функций
| Функция | Вид уравнения | Способы замены переменных | Линеризованное уравнение |
| Гиперболическая | 
| Заменяем

|

|
| Степенная | 
| 1.логарифмируем
 2.заменяем
2.заменяем



|

|
| Экспоненциальная | 
| 1.логарифмируем
 2.заменяем
2.заменяем


|

|
| Логистическая | 
| 1.преобразуем
 2.заменяем
2.заменяем

| 
|
| Простая модифицированная экспоненциальная | 
| заменяем

| 
|
Для оценки правильности выбора аналитической зависимости  наряду с вариациями расчетных значений по отношениям к исходным уровням динамического ряд, индексом корреляции и коэффициентом детерминации используется также и специальный показатель – критерий Р.Фишера (F). F-критерий определяется по формуле
наряду с вариациями расчетных значений по отношениям к исходным уровням динамического ряд, индексом корреляции и коэффициентом детерминации используется также и специальный показатель – критерий Р.Фишера (F). F-критерий определяется по формуле
|
|
|
 , (17)
, (17)
где  -факториальная дисперсия, характеризующая вариацию
-факториальная дисперсия, характеризующая вариацию  за счет фактора t;
за счет фактора t;
 - остаточная дисперсия, характеризующая отклонения между исходными и расчетными значениями переменной
- остаточная дисперсия, характеризующая отклонения между исходными и расчетными значениями переменной  .
.
Дисперсии  и
и  определяются путем деления суммы квадратов отклонений не на количество уровней динамического ряда, а на число степеней свободы. Эти расчеты ведутся по формулам:
определяются путем деления суммы квадратов отклонений не на количество уровней динамического ряда, а на число степеней свободы. Эти расчеты ведутся по формулам:
 ; (18)
; (18)
 . (19)
. (19)
где N –количество констант в уравнении регрессии;
n – количество элементов в динамическом ряду.
Правильность выбора уравнения тренда определяется сравнением F -критерия, рассчитанного по формуле (17) с табличной величиной  (см.приложение 1). Табличное значение критерия Р.Фишера устанавливается для
(см.приложение 1). Табличное значение критерия Р.Фишера устанавливается для  и
и  степеней свободы и выбираемой доверительной вероятности (Р). Доверительная вероятность определяет степень достоверности суждения о возможных значениях статистических характеристик. Чаще всего используется доверительные вероятности Р=0,95 или Р=0,99.
степеней свободы и выбираемой доверительной вероятности (Р). Доверительная вероятность определяет степень достоверности суждения о возможных значениях статистических характеристик. Чаще всего используется доверительные вероятности Р=0,95 или Р=0,99.
Степени свободы рассчитываются по формулам:
 ; (20)
; (20)
 . (21)
. (21)
Если F окажется больше F т, то уравнение тренда можно использовать для описания закономерности  .
.
Экстраполяция одиночных динамических рядов позволяет установить точечные значения переменной  на перспективу. Однако в следствии того, что отсутствует функциональная связь между показателем
на перспективу. Однако в следствии того, что отсутствует функциональная связь между показателем  и временем t, реальная величина переменной
и временем t, реальная величина переменной  после окончания периода упреждения может отличаться от прогнозной. Эти отклонения могут возникнуть по ряду причин:
после окончания периода упреждения может отличаться от прогнозной. Эти отклонения могут возникнуть по ряду причин:
- из-за того, что уровни временного ряда представляют не генеральную, а выборочную совокупность – так называемую выборку;
- воздействием на прогнозируемый показатель не только аргумента t, но и множества факторов, не включенных в уравнение.
Эти обстоятельства требуют выполнения специальной проверки результатов прогнозирования.
В ходе такой проверки решаются две задачи по оценке пригодности уравнения, построенного по выборочным данным, и определение возможных отклонений от точечного прогноза, полученного методом экстраполяции функции.
|
|
|
Статистическая значимость параметров уравнения тренда выполняется на основе расчета доверительной зоны выборочной линии регрессии, в рамках которой может располагаться линия тренда.
Для уравнения линейной зависимости -  построение доверительной зоны выполняется в следующем порядке:
построение доверительной зоны выполняется в следующем порядке:
- определяется значимость параметров «а» и «b» по формулам:
 ; (22)
; (22)
 , (23)
, (23)
где  - случайная ошибка параметра «a»;
- случайная ошибка параметра «a»;
 - случайная ошибка параметра «b»;
- случайная ошибка параметра «b»;
 - остаточное среднее квадратическое отклонение, рассчитываемое по формуле:
- остаточное среднее квадратическое отклонение, рассчитываемое по формуле:
 ; (24)
; (24)
- оцениваются расхождения между уравнениями выборочной и генеральной совокупности по t – критерию Стьюдента. Значение этого критерия рассчитывается по формулам:
 ; (25)
; (25)
 . (26)
. (26)
Полученные  и
и  сравниваются с табличными t т, найденными для K=n-2 степеней свободы и принятой вероятности 0,95 или 0,99 (см.приложение 2). Если t ф > t т, то параметры «а» и «b» считаются статистически значимыми и могут быть использованы для расчета переменной
сравниваются с табличными t т, найденными для K=n-2 степеней свободы и принятой вероятности 0,95 или 0,99 (см.приложение 2). Если t ф > t т, то параметры «а» и «b» считаются статистически значимыми и могут быть использованы для расчета переменной  . Если t ф < t т, то расхождения
. Если t ф < t т, то расхождения  от линии регрессии, полученной по всей генеральной совокупности, недопустимо велики;
от линии регрессии, полученной по всей генеральной совокупности, недопустимо велики;
- находятся доверительные границы параметров «а» и «b» по формулам:
 ; (27)
; (27)
 . (28)
. (28)
Зная 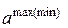 и
и  , можно в пределах точности выбранной вероятности утверждать, что в генеральном уравнении тренда, т.е. уравнении, построенном по всей генеральной совокупности признаков временного ряда, параметры «а г» и «b г» принимают одно из значений:
, можно в пределах точности выбранной вероятности утверждать, что в генеральном уравнении тренда, т.е. уравнении, построенном по всей генеральной совокупности признаков временного ряда, параметры «а г» и «b г» принимают одно из значений:
 и
и  .
.
Для графического отображения доверительной зоны для каждого значения t по формуле (29) определяют ординаты точек по верхней и нижней граничным кривым ( ).
).
 , (29)
, (29)
где  , (30)
, (30)
 .
.
Расположение граничных кривых определяется путем соединения плавными линиями отдельно точек  и
и  .
.
На точность прогноза оказывает воздействие не только расхождения между константами («а» и «b») уравнений, построенных по выборочным совокупностям. Конечный результат зависит также и от величины отклонений между расчетными значениями признака -  и их фактическими уровнями -
и их фактическими уровнями -  .
.
Для определения интервала колеблемости переменной на момент прогноза необходимо к уже рассмотренным источникам вариации (колеблемость параметров «а» и «b») добавить отклонения фактических значений переменной  по отношению к точкам на линии регрессии
по отношению к точкам на линии регрессии 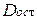 .
.
Доверительные интервалы для индивидуальных значений признака определяются по формуле:
 , (31)
, (31)
где 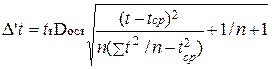 . (32)
. (32)
Зная  , можно с заданным уровнем вероятности утверждать, что фактическое значение прогнозируемой величины не выйдет за пределы доверительных интервалов.
, можно с заданным уровнем вероятности утверждать, что фактическое значение прогнозируемой величины не выйдет за пределы доверительных интервалов.
|
|
|
4.2 Этапы экспертного прогнозирования. Поскольку именно с помощью экспертного прогнозирования может быть решена большая часть проблем, возникающих при разработке прогнозов, рассмотрим в систематизированном виде основные этапы экспертного прогнозирования.
1. На стадии подготовки к разработке прогноза должны быть решены следующие задачи:
1) Подготовлено организационное обеспечение разработки прогноза;
2) Сформулировано задание на прогноз;
3) Сформированы рабочая и аналитические группы сопровождения;
4) Сформирована экспертная комиссия;
5) Подготовлено методическое обеспечение разработки прогноза;
6) Подготовлена информационная база для проведения прогноза;
7) Подготовлено компьютерное сопровождение разработки прогноза.
После того, как принято решение о разработке прогноза, необходимо определить исполнителей, которым разработка будет поручена.
С одной стороны, это группа работников, которой поручается организационное обеспечение разработки прогноза, с другой стороны, - это группа специалистов, которая должна обеспечить методическое и информационное его сопровождение.
От хорошей подготовки и профессионального уровня разработчиков прогноза зависит его качество.
Действительно, поскольку качественный экспертный прогноз может быть разработан лишь в том случае. Если он хорошо подготовлен, если в его разработке задействованы компетентные специалисты, если использована достоверная информация, если оценки получены корректно и корректно обработаны.
|
|
|
12 |


