 |
Уравнение состояния и закономерности движения газа
|
|
|
|
Из термодинамики известно, что для равновесных систем состояние газа является определенным, если известны его основные параметры: давление, плотность, температура.
Для совершенных (идеальных) газов, у которых объем молекул пренебрежимо мал по сравнению с объемом, занимаемым газом, справедливо уравнение Менделеева-Клайнерона
, (1.1)
где р – абсолютное давление; r – плотность; Т – абсолютная температура; R – газовая постоянная, равная для воздуха 287 Дж/(кг×К).
Для промышленных пневмосистем, работающих при давлении много меньше 10 МПа, воздух можно рассматривать как идеальный газ и при расчетах использовать уравнение (1.1).
Из уравнения (1.1) выводятся уравнения состояния газа при различных термодинамических процессах.
Если ввести понятие удельный объем w, под которым понимается объем газа, занимаемый единицей массы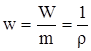 
, то для
изотермического процесса pw = const;
изобарного процесса 
;
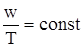изохорного процесса 
.
В пневмосистемах возможны различные условия теплообмена между газом и окружающей средой. Например, при малых скоростях течения газа в трубе с хорошим теплообменом процесс вполне можно рассматривать как изотермический.
Если процесс изменения параметров газа протекает быстро и теплообменом с окружающей средой практически можно пренебречь, то такой процесс называется адиабатным и описывается уравнением:
pwk = const или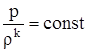 
,
где k – показатель адиабаты, равный отношению удельных теплоемкостей газа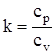 
, для воздуха можно принять k = 1,4.
Однако в общем случае в зависимости от конкретных условий процессы изменения параметров газа могут протекать с произвольным теплообменом. Такие процессы называются политропическими и характеризуются уравнением
|
|
|
pwn = const или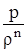 
= const,
где n – показатель политропы газа, величина которого обычно находится в пределах k 
n> 1.
Для некоторых газов при давлении, превышающем 10 МПа, n > k и может достигать значения n = 2 и более.
Для политропических процессов соотношение между давлением р, температурой Т, удельным объемом или плотностью можно выразить как
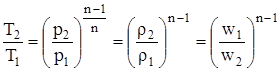. (1.2)
Эта формула будет справедлива и для адиабатического процесса при замене показателя политропы n на показатель адиабаты k.
Приведенные уравнения справедливы лишь для равновесных систем. При движении газа система будет неравновесной. Кроме параметров р, r, Т добавится еще и скорость течения газа V.
Рассмотрим особенности установившегося течения газа в пневмоси-стемах, которые необходимо учитывать при истечении газа через отверстие, при заполнении или опорожнении емкостей, при течении по трубам и через местные сопротивления.
При установившемся течении массовый расход газа одинаков во всех сечениях вдоль потока.
Qm =r∙V∙S = const,
где S – площадь сечения потока; V – скорость течения газа.
В отличие от течения несжимаемой жидкости, для газа не сохраняется постоянство объемного расхода Q, а расход увеличивается вследствие расширения, вызванного понижением давления вдоль потока, а расширение приводит к изменению температуры (1.1). Поэтому уравнение Бернулли для идеального газа отличается от уравнения для идеальной жидкости. Если не учитывать разность нивелирных высот z1 и z2, поскольку плотность газа мала (для воздуха при атмосферном давлении r = 1,29 кг/м3), то уравнение Бернулли для политропического процесса можно записать в таком виде
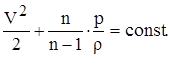(1.3)
Воспользуемся уравнением Бернулли (1.3) для определения скорости истечения газа через отверстие площадью 
(рис. 1.1).
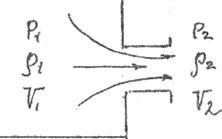
Рис. 1.1. Истечение газа через отверстие
Считая скорость V1 равной нулю и не пренебрегая потерями при истечении, получим
|
|
|
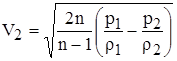
где p1 и p2 – давление газа, соответственно, в резервуаре и в среде, в которую происходит истечение, или, в общем случае, давление в начале и конце газового потока. Если учесть, что согласно соотношениям (1.2)
, (1.4)
то, проведя алгебраические преобразования, массовый расход газа, протекающего со скоростью V через сечение площадью S, можно определить по формуле:
В большинстве промышленных пневмосистем происходит адиабатный процесс изменения параметров воздуха или политропический процесс, когда показатель политропы n близок по своему значению к показателю адиабаты k = 1,4. Поэтому в формулу (1.4) для практических расчетов целесообразно вместо n подставить показатель адиабаты k. Кроме того, в реальных потоках воздуха через отверстия существуют потери, которые, как и при истечении несжимаемой жидкости, учитываются коэффициентом расхода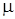 
, представляющим собой отношение реального расхода к теоретическому.
С учетом сказанного, а также используя уравнение состояния (1.1), преобразуем формулу (1.4) в общую формулу расчета массового расхода воздуха через отверстие площадью S
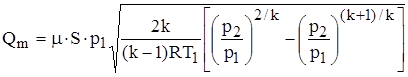. (1.5)
При p2/p1 = 0 и p2/p1 = 1 массовый расход Qm равен 0. Следовательно, значение p2/p1, при котором массовый расход Qm будет максимальный, можно получить, приравняв производную функции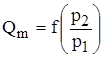 
к нулю.
В результате максимальный массовый расход Qm будет при:
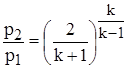(1.6)
Это значение для воздуха при k = 1,4 равно 0,528.
На рис. 1.2 пунктиром приведен график, соответствующий функции (1.5). На этом же графике сплошной линией показана реальная, экспериментально подтвержденная зависимость, полученная при условии p1 = const.
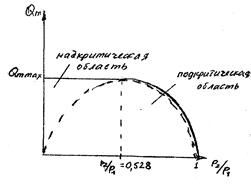
Рис. 1.2. Теоретическая и реальная характеристики истечения газа
Очевидно, что в диапазоне 0,528 <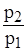 
< 1 теоретическая и реальная зависимости совпадают, а в диапазоне 0 < 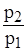< 0,528 существенно расходятся, причем массовый расход Qm в этой области не зависит от перепада давлений и остается постоянным, равным максимальному.
Отношение 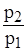= 0,528 получило название “критическое” 
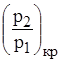. Скорость течения воздуха V2 при таком отношении давлений равна скорости звука, которая для идеального газа определяется формулой 
.
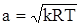Для воздуха при k = 1,4 и Т= 293°К получим а = 347 м/с. Поэтому при течении газа всегда рассматриваются две области:
|
|
|
а) докритическая (дозвуковая), для которой массовый расход определяется формулой (1.5);
б) закритическая (сверхзвуковая), для которой массовый расход определяется по следующей формуле, полученной путем подстановки в формулу (1.5) значения из формулы (1.6):
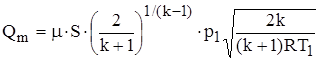. (1.7)
|
|
|
