 |
Дифференциальные уравнения в частных производных и метод разделения переменных
|
|
|
|
О математическом описании многомерных систем
Конфигурационное пространство
Ознакомившись со свойствами волновых функций и уровней одномерных стационарных систем, мы сделали лишь первый шаг к оформлению математических основ теории химической связи. Далее предстоит рассмотрение стационарных пространственных движений одной частицы. Такие модели реалистичнее передают черты физических явлений, но это связано с усложнением математического аппарата.
При переходе к описанию пространственного движения частицы число координат возрастает до трёх, т.е. конфигурационное пространство переменных в этом случае – обычное трёхмерное пространство, соответствующее трём степеням свободы. Геометрические образы волновых функций подобны образам полей, распределенным в объёме. Если же система содержит не одну, а две частицы, то независимых пространственных координат уже шесть, конфигурационное пространство шестимерно. Не следует считать, что это какая-то исключительная ситуация: атом водорода содержит два частицы – ядро и электрон, и эта система полностью описывается с помощью 6 координат. При переходе к N-частичной системе размерность конфигурационного пространства соответственно увеличивается до ЗN.
Геометрическая наглядность при анализе волновых функций таких многомерных систем недостижима. Поэтому для химии особенно важны такие модели, которые допускают построение наглядных графических образов. Этому условию отвечает пространственное движение одной частица.
Дифференциальные уравнения в частных производных и метод разделения переменных
4.1.2.1. Многие фундаментальные теоретические модели физики построены с использованием математического аппарата теории дифференциальных уравнений в частных производных. Напомним читателю, что само понятие частной производной восходит к стремлению изучить поведение многомерной функции при изменении лишь одной из независимых переменных без затрагивания прочих. Сложная многомерная проблема как бы разделяется на набор одномерных задач, которые по отдельности намного легче поддаются анализу. Позволим себе сравнить ситуацию с многоголосием в музыкальном произведении: каждая одноголосная партия проста, и её может воспроизвести даже нёискушенный исполнитель, но полифония требует уже изрядной подготовки.
|
|
|
4.1.2.2. Уравнение Шредингера относится к числу дифференциальных уравнений в частных производных второго порядка. В принципе оно должно включать все координаты каждой из частиц в качестве аргументов, т.е. соответствующее конфигурационное пространство 3N–мерно. Сложность решения уравнения Шредингера возрастает с увеличением числа переменных, поэтому необходимы физически обоснованные способы упрощения задач такого рода. К счастью, существует очень простой и эффективный прием, называемый методом разделения переменных, который предложен Фурье. Обсудим кратко основы этого метода.
4.1.2.3. Для простоты рассмотрим всего две независимые переменные  и определим в таком конфигурационном пространстве, во-первых, некоторую функцию F или семейство функций и, во-вторых, некоторый линейный оператор
и определим в таком конфигурационном пространстве, во-первых, некоторую функцию F или семейство функций и, во-вторых, некоторый линейный оператор  . Этот оператор может содержать в качестве слагаемых и сами переменные, и функции от них, например,
. Этот оператор может содержать в качестве слагаемых и сами переменные, и функции от них, например,  , и операторы частного дифференцирования первого порядка
, и операторы частного дифференцирования первого порядка  и
и  , и второго порядка, включая перекрёстное дифференцирование, т.е.
, и второго порядка, включая перекрёстное дифференцирование, т.е.  . Вообще говоря, можно и не ограничиваться вторым порядком дифференцирования, но для наших задач его достаточно. Перед производными в качестве коэффициентов могут быть также функции от переменных х и у. Так что дифференциальное уравнение для семейства функций представится в виде
. Вообще говоря, можно и не ограничиваться вторым порядком дифференцирования, но для наших задач его достаточно. Перед производными в качестве коэффициентов могут быть также функции от переменных х и у. Так что дифференциальное уравнение для семейства функций представится в виде
|
|
|
 . (4. I)
. (4. I)
4.1.2.4. В самом простом случае для разделения переменных в уравнении (4.1) необходимо, чтобы оператор  допускал группировку всех выражений и действий над каждой из переменных в отдельные слагаемые, например
допускал группировку всех выражений и действий над каждой из переменных в отдельные слагаемые, например 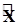 и
и  . Вводимые нами символы операторов красноречиво указывают на преобразуемые ими переменные и не требуют дополнительных пояснения. Итак, оператор
. Вводимые нами символы операторов красноречиво указывают на преобразуемые ими переменные и не требуют дополнительных пояснения. Итак, оператор  должен быть представлен в аддитивной форме
должен быть представлен в аддитивной форме
 (4.2)
(4.2)
Для разделения переменных в дифференциальном уравнении (4.1) искомую функцию F(x,y) следует представить в виде произведения двух сомножителей X(x) и Y(у), каждый из которых является неизвестной функцией лишь одного аргумента:
 , (4.3)
, (4.3)
или 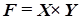
|
|
|


