 |
Решетки со стековой модуляцией.
|
|
|
|
Сейчас посмотрим на решетки, модулированные стеками. Схематически они выглядят примерно так:
2.2 2.2 2.2 2.2 2.2 2.2 2.2
 |
1.44 1.44 1.44 1.44 1.44 1.44 1.44
Рисунок 3. Схематичное представление одного стека бинарных
структур.
То есть в стеке происходит постепенное утолщение с последующим уменьшением толщины слоев с одним показателем преломления, и обратные этим изменения для слоев с другим показателем преломления.
Что это такое станет более очевидным, если посмотреть на графики № 19 и № 22.
График 19. Схематичное изображение оптического пути для
трехстековой модулированной структуры из ста слоев.
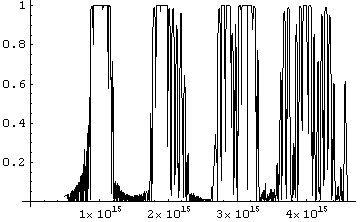
График 20. Зависимости отражения волны для
трехстековой модулированной структуры из ста слоев
при угле падения 00 от частоты.
График 21. Зависимости отражения волны для
трехстековой модулированной структуры из ста слоев
при угле падения 450 от частоты.
График 22. Схематичное изображение оптического пути для
пятистековой модулированной структуры из ста слоев.
График 23. Зависимости отражения волны для
пятистековой модулированной структуры из ста слоев
при угле падения 00 от частоты.
График 24. Зависимости отражения волны для
пятистековой модулированной структуры из ста слоев
при угле падения 450 от частоты.
Очень интересным представляется плато в области 1*1015 Гц при угле падения 00. То, что эта частота не является рабочей для лазеров, не должно пугать, ибо всегда можно ее сместить изменением толщины всех слоев (не меняя при этом отношения толщин между соседними). Но при увеличении угла падения, это плато расщепляется на несколько узких пиков, которые расплываются в сторону увеличения частоты.
|
|
|
Такая дисперсия может помешать управлению излучением, но в этом видятся некие другие возможности.
Бинарные решетки с гауссовыми модуляциями.
Ну и, наконец, последняя из предложенных модуляций – модуляция по функции Гаусса.
На самом деле здесь возможно два варианта (рисунок № 4 и рисунок № 5, график № 25 и графики № 26 и № 27). Для порядка вкратце рассмотрим оба. Первый из них (рисунок № 4 и график № 25) назовем псевдогауссовым, ввиду того, что параметр (в нашем случае – оптический путь) сначала уменьшается, а потом увеличивается, то есть функционально изменяется обратно функции Гаусса.
Схематически псевдогауссову модуляцию можно изобразить следующим образом:
2.2 2.2 2.2 2.2 2.2 2.2 2.2
 |
1.44 1.44 1.44 1.44 1.44 1.44 1.44
Рисунок 4. Схематичное представление структура с псевдогауссовой
модуляцией.
То есть происходит одновременное утолщение и утоньшение слоев с разными показателями преломления.
Оптический путь такой структуры схематично представлен на графике № 25.
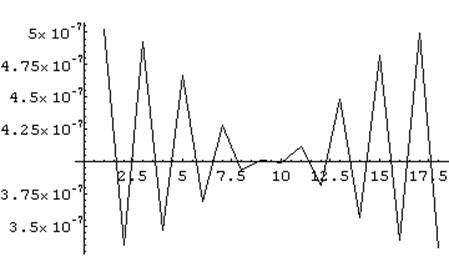
График 25. Схематичное изображение оптического пути для
псевдогауссовой модуляции структуры.
Второй вариант – сначала утолщение, а потом утоньшение (но обязательно одновременное для слоев с разными показателями преломления) по функции Гаусса, как это показано на рисунке 5.
|
|
|
2.2 2.2 2.2 2.2 2.2 2.2 2.2
 |
1.44 1.44 1.44 1.44 1.44 1.44 1.44
Рисунок 5. Схематичное представление структура с гауссовой
модуляцией.
Оптический путь при такой модуляции схематично показан на графике № 26 и графике № 27.
График 26. Схематичное изображение оптического пути для
гауссовой модуляции структуры (малое число слоев (18)).
График 27. Схематичное изображение оптического пути для
гауссовой модуляции структуры (большое число слоев (46)).
При псевдогауссовой модуляции появляется довольно беспорядочный набор узких пиков, чередующихся с сильно возмущенными зонами, с коэффициентом отражения от 0.2 до 0.7. И вся эта картинка «плавает» и диспергирует в зависимости от угла падения излучения. Приводить ее здесь не будем. Сейчас перейдем непосредственно к бинарным структурам, промодулированным с помощью функции Гаусса exp(-x2/s2), где параметр s = L/4. Здесь L – ширина всей структуры.
Поскольку все схематические изображения в данном случае выглядят так же, как на графиках № 26 и 27 только с разным числом слоев, не будем приводить их в дальнейшем.
Восьмислойная структура дает следующие результаты:
График 28. Зависимости отражения волны для
структуры из восьми слоев при угле падения 00 от частоты.
График 29. Зависимости отражения волны для
структуры из восьми слоев при угле падения 450 от частоты.
Получается довольно интересная картина. Четко вырисовывается пик на нужной частоте: 2*1015 – 2.5*1015 Гц. При этом подавляется отражение на смежных частотах. Подводит только малый коэффициент отражения. 0.8 для 00 падения и совсем малый 0.3 при 450 падения луча. Попробуем увеличить их за счет увеличения числа слоев.
График 30. Зависимости отражения волны для структуры
из восемнадцати слоев при угле падения 00 от частоты.
График 31. Зависимости отражения волны для структуры
из восемнадцати слоев при угле падения 450 от частоты.
|
|
|
Результат существенно улучшился. Но теперь ухудшилось пропускание на соседних частотах. Появляется бахрома с разбросом коэффициента отражения до 0.15.
Чтобы уловить общую тенденцию этого направления оптимизации посмотрим еще несколько графиков, постепенно увеличивая число слоев в решетке.
График 32. Зависимости отражения волны для структуры
из тридцати шести слоев при угле падения 00 от частоты.
График 33. Зависимости отражения волны для структуры
из тридцати шести слоев при угле падения 450 от частоты.
Теперь бахрома в области пропускания стала чаще. Посмотрим, что дальше будет.
График 34. Зависимости отражения волны для структуры
из пятидесяти шести слоев при угле падения 00 от частоты.
График 35. Зависимости отражения волны для структуры
из пятидесяти шести слоев при угле падения 450 от частоты.
Так выглядит частотный профиль отражения бинарной квазипериодической решетки при пятидесяти шести слоях в структуре. Дальнейшее увеличение числа слоев практически не изменяет пики отражения. Это видно, например, из графиков № 36 и № 37.
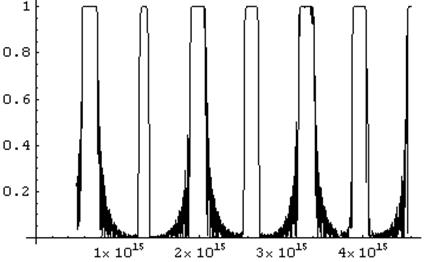
График 36. Зависимости отражения волны для структуры
из шестидесяти четырех слоев при угле падения 00 от частоты.
График 37. Зависимости отражения волны для структуры
из шестидесяти четырех слоев при угле падения 450 от частоты.
Вполне очевидно, что пики существенно не изменились, увеличилась частота бахромы в зоне пропускания. Профиль отражения становится вполне устойчивым примерно с сорока – пятидесяти слоев (в зависимости от того насколько требуется подавить или участить бахрому в области пропускания.). Видимо, это предел «хорошести» для отражения решетки при данной модуляции. Наверняка для улучшения этого профиля требуется либо смягчение ограничений, накладываемых на условие (возможность применения других материалов, например), либо некая принципиально другая идея для создания решетки. Интересно, что, начиная даже с малого числа слоев (около двадцати), на интересующей нас частоте наблюдается расщепление пика справа при увеличении угла падения. И, начиная с тридцати слоев, вторичная мода справа при угле падения излучения 450 становится неизменной.
|
|
|
Заключение.
Предложенные методы модуляции бинарных квазипериодических анизотропных структур дают метод практического решения некоторых задач, связанных с передачей излучения и его управлением.
В первую очередь хотелось бы отметить некоторые общие закономерности. Что характерно для любой оптимизирующей структуры: луч, направленный со стороны более тонких слоев, дает лучший профиль отражения при малых углах падения, но который сильнее расплывается и дробится на множество пиков при увеличении этого угла. Луч же, направленный со стороны более широких слоев (нисходящие ступени и псевдогауссова модуляция), хотя и дает несколько худший профиль (что можно пытаться исправить другими методами), зато является более устойчивым к изменению угла падения. Также важно отметить четкую зависимость расположения пиков отражения от базовой толщины слоев (от оптического пути вообще). Так, если будет замечена устойчивая, хорошая область отражения в диапазоне, не соответствующем условию задачи, варьируя оптические пути (технологически – толщины слоев), можно сместить его до уровня нужных частот.
Теперь непосредственно по различным модуляциям. В зависимости от поставленной задачи, можно дать несколько рекомендаций. Так, если требуется хорошее отражение при малых углах падения, можно использовать ступенчатую модуляцию (графики № 11, № 14 и № 17), но, если требуется узкая направленность (полное отсутствие отражения при других углах), лучше использовать стековую модуляцию (графики №№ 20, 21 и №№ 23, 24). С другой стороны, если требуется совсем узкая частотная полоса, лучше использовать большие углы падения луча (близкие к 450) при той же стековой модуляции (графики № 21 и № 24). Сознательно стараемся избегать гауссовой модуляции всего лишь ввиду более трудоемкого производства таких элементов в технологическом смысле, так как требуется большая точность в толщине слоев и большее число самих слоев, напыляемых (или выращиваемых) на подложке.
Однако именно при этой модуляции достигнуты наиболее значимые результаты. Так, например, видится готовое узкополосное зеркало, отражающее при любых углах падения (от 00 до 450) (графики №№ 30, 31, №№ 32, 33, №№ 34, 35 и №№ 36, 37). Опять таки, варьируя общую толщину решетки, можно смещать отражаемую частоту вправо или влево, в зависимости от поставленных целей (источника излучения, например). Даже структуры, в которых зоны отражения зависят от угла падения излучения, могут найти себе применение (первые пики в решетках с гауссовой модуляцией). Например, пусть имеется источник белого или почти белого света (в том смысле, что присутствует довольно широкий спектр излучения), а нужна некоторая более узкая частотная полоса. Тогда достаточно модулированную по гауссу решетку просто расположить под необходимым углом к падающему лучу. Волны с требуемой частотой отразятся, а остальные пропустятся. Конечно, лучше выглядит первый пик при стековой модуляции (график № 20), и, чтобы вырезать нужную частоту, можно взять такую решетку и расположить ее перпендикулярно лучу. Но тогда для другой полосы частот требуется другая структура (другой толщины). Таким образом, под рукой придется иметь целый набор стековых решеток. В то время как гауссову структуру достаточно повернуть на нужный угол.
|
|
|
Та же идея может быть применена, если есть разнонаправленное излучение (от нескольких источников или сильно расходящиеся лучи) и необходимо выделить некоторое направление. Тогда можно, расположив структуру на поглощающей подложке, расположить ее под нужным углом. Часть излучения отразится в нужном направлении, а остальная часть – пропустится или поглотится.
В качестве дальнейшего направления исследований видится применение, возможно, смешанных модуляций, с перспективой получения более широких зон отражения, либо узких пиков, но с абсолютным пропусканием на остальных частотах (сглаживание бахромы и получение более вертикальных стенок профиля).
Предложенные методы модуляции могут найти применение в квантовой электронике и других разделах физики и техники, где существенную роль играет узкая частотная полоса излучения, а так же могут служить для создания селективных управляемых фильтров, зеркал и затворов.
Приложение.
При проведении вычислений настоящей работы и построении графиков использовался прикладной пакет «Mathematica 3.0». Этот пакет является достаточно мощным средством для решения многих задач линейной алгебры. Основными его достоинствами являются простота в использовании, удобный, интуитивно понятный интерфейс, большой спектр возможностей и богатейший хелп. Как особенность хочется подчеркнуть отсутствия у пакета компилятора.
Ниже приведен листинг программы, выполняющей все расчеты и построения, относящиеся к данному проекту.
Листинг программы к данному проекту.
В этой части программы подключается модуль пакета, работающий с матрицами, и задаются начальные диады и скорость света.
Здесь задаются свойства системы: число периодов решетки, базовые толщины слоев (от этих значений потом строится матрица слоев), показатели преломлений сред. Потом задается распределение Гаусса с последующей дискретизацией, ибо компьютер не умеет обращаться с непрерывными функциями. В случае не гауссовой модуляции вместо распределения Гаусса следует вводить требуемую функцию распределения значений толщин слоев.
В этой части были заданы значения показателя преломления n, вектор рефракции m, векторы a и b и вычислялись диады этих векторов.
После чего было вычислено значение Н 0 для последующего вычисления оператора отражения формальным образом.
В следующем блоке (приведенном ниже) происходит вычисление характеристической матрицы для одного слоя решетки.
Здесь вводятся операторы импеданса и вычисляются операторы пропускания H d и отражения H r. Осталось только построить графики при 00 и при 450 падения излучения, что и делается в последнем блоке (ниже). При желании можно ввести ту же команду, заменив Н r на Н d. Тогда построятся профили пропускания, а не отражения.
Список использованной литературы.
1. H.-H. Tung and C.-P. Lee, IEEE J. Quant. Electr. 32 (3), 507 – 512 1996г.
2. Д. В. Богомолов. Оптимизация профиля пропускания частотных
фильтров излучения с использованием модулированных
сверхрешеток. Курс. работа. Минск, БГУ, КМПФиИ, 1999г.
3. Л. М. Барковский, Г. Н. Борздов, Ф. И. Федоров. Волновые операторы
в оптике. Минск, АН, институт физики, 1983г.
4. Л. М. Барковский, Г. Н. Борздов, А. В. Лавриненко. Френелевские
операторы отражения и пропускания для плоскослоистых
гироанизотропных сред. Вести АН БССР, сер. физ-мат наук,
1986г., №2, стр. 79 – 84.
5. М. Борн, Э. Вольф. Основы оптики. Москва, «Наука», 1988г.
6. А. Ярив, П. Юх. Оптические волны в кристаллах. Москва, «Мир»,
7. Ф. Р. Гантмахер. Теория матриц. Москва, «Наука», 1988г.
8. Ф. И. Федоров. Оптика анизотропных сред. Минск, АН БССР, 1958г.
9. Ф. И. Федоров. Теория гиротропии. Минск, «Наука и техника», 1976г.
10. Ф. И. Федоров, Л. М. Барковский, Г. Н. Борздов, Ю. Э. Камач,
В. М. Овчинников. Расчет пропускания оптических каналов с произвольно ориентированными анизотропными элементами. I. Операторы пропускания и отражения для одной границы раздела. Вести АН БССР, сер физ-мат наук, 1982г., №3, стр. 59 – 64.
11. Г. Н. Борздов, Л. М. Барковский, В. И. Лаврукович. Тензорный
импеданс и преобразование световых пучков системами анизотропных слоев. П. Косое падение. ЖПС, 1976г., т.25, вып.3, стр. 526 – 531.
12. D. W. Berreman. Optics in stratified and anisotropic media: 4x4- matrix
formulation. Jorn. Optics Soc. Amer., 1972, v. 62, №4, p. 502 – 510.
13. А. В. Лавриненко, Д. Н. Чигрин, Д. В. Богомолов. Оптимизация
профиля пропускания частотных фильтров излучения с использованием модулированных сверхрешеток. Квантовая электроника. Материалы II Межгосударственной н-т. конференции. Минск, 23 – 25 ноября, 1998г., стр. 108.
14. Г. С. Ландсберг. Оптика. Москва, «Наука», 1976г. гл. 23
стр. 470 – 489.
15. Mathematica 3.0. Users guide & help.
|
|
|
12 |
