 |
Рассмотрим некоторые примеры.
|
|
|
|
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
1. Составим таблицу истинности и функциональную схему для структурной формулы 
, которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:
| Переменные | Промежуточные логические формулы | Формула | |||||
| 
| 
| 
| 
| 
| 
|
|
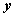
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.
Функциональная схема.
2. Составим таблицу истинности и функциональную схему для структурной формулы 
.
Таблица истинности.
| Переменные | Промежуточные логические формулы | Формула | ||||
|
|
|
| 
| 
| 
|
|
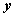
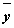
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.
Функциональная схема.
3. Таблица истинности для структурной формулы 
:
| Переменные | Промежуточные логические формулы | Формула | ||||||
|
|
| 
|
| 
| 
|
| 
|
|
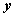
Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
|
|
|
Функциональная схема:
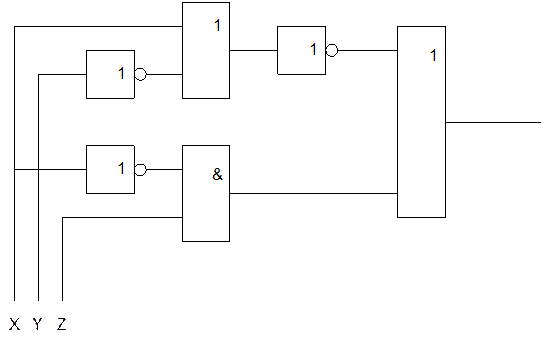
Упрощение формул.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) 
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);
2) 
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);
3) 
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания);
|
|
|
4) 
(вводится вспомогательный логический сомножитель (
); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
5) 
(сначаладобиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
6) 
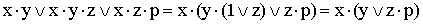
(выносятся за скобки общие множители; применяется правило операций с константами);
7) 
(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания);
8) 
(общий множитель x выносится за скобки, комбинируются слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции 
применяется правило операции переменной с её инверсией);
9) 
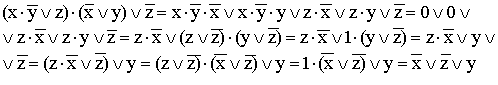
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);
10) 
(используются правило де Моргана, закон двойного отрицания и закон поглощения).
Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге. Навыки приходят с опытом.
Очевидно, что дом гораздо быстрее построить из блоков, чем из кирпича. Что то похожее наблюдается и в вычислительной технике. В принципе, можно построить сложные электронные устройства из рассмотренных элементов: И, ИЛИ, НЕ, но значительно удобнее использовать детали более крупные. Каждая такая деталь в целом выполняет вполне определенные функции, что и закрепило за ними название электронные функциональные элементы и устройства. Системы из таких автономных функциональных блоков проще конструировать, налаживать, обслуживать и ремонтировать.
|
|
|
