Вывод основного уравнения аэродинамики

 

Вокруг нас так много необыкновенного, что можно открывать новое в окружающем нас мире, лишь используя логику и здравый смысл. В физике, изучающей законы природы, до сих пор есть огромные белые пятна, например, не сформулированы основные законы физики в самых разных разделах. Например, до сих пор не сформулированы основные законы аэрогидростатики и аэрогидродинамики.

В аэрогидродинамике есть необъяснимое, с точки зрения физики, но очень важное физическое явление – возникновение подъёмной силы крыла самолёта. Подъёмная сила крыла самолёта возникает при его обтекании воздухом. Основной закон аэродинамики должен объяснять это физическое явление, но он впервые сформулирован только в этой публикации. Известно, что чем выше скорость потока воздуха вдоль поверхности крыла, тем меньше давление воздуха на крыло, но не известно, почему это происходит.

Этот пробел теории легко устранить самостоятельно. Для этого нужно вывести основное уравнение аэрогидродинамики, которое объяснит причину возникновения этого физического явления, и покажет взаимную зависимость трёх основных величин аэродинамики - полного давления газа, динамического давления и статического давления.

При отсутствии движения газа относительно твёрдой поверхности давление газа является вектором, направленным перпендикулярно к поверхности. Если мы приложим усилие, и начнем двигать газ относительно поверхности или с усилием проталкивать газ через трубку, наши усилия не пропадут даром. Возникнет малопонятный физический эффект: чем быстрее газ будет двигаться, тем меньшее давление его молекулы будут оказывать на поверхность. Причина возникновения этого эффекта до сих пор не объяснена.

Сейчас в физике есть уравнение, частично объясняющее это физическое явление, это уравнение для движения идеальной несжимаемой жидкости (без внутреннего трения), выведенное швейцарским физиком Д. Бернулли (опубликовано в 1738 г.). Это уравнение выведено из закона сохранения энергии всего для двух из трёх величин - динамического и статического давлений. Его невозможно применять для газа, поскольку несжимаемых газов не бывает. Очень странно, что уравнение Бернулли почти за три века своего существования так и не было преобразовано в основной закон аэродинамики, поскольку задача достаточно проста, нужно просто изменить подход.

Самое простое и наглядное решение этой задачи возможно при помощи векторной алгебры.

В аэродинамике мы имеем дело с векторами (давление это сила, с которой газ давит на единицу площади). У нас есть три вектора:

1. Статическое давление на поверхность . Направлено перпендикулярно поверхности.

2. Динамическое давление движения газа , заставляющее газ двигаться вдоль поверхности. Направлено горизонтально вдоль поверхности.

3. Полное давление газа . Является их векторной суммой.

 

 

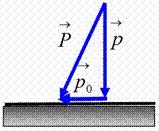Поверхность

 

Рис. 1

 

Для движения газа вдоль поверхности можно составить векторное уравнение:

 

(1)

Т.е. полное давление равно сумме динамического и статического давления.

Из рисунка видно, что чем больше мы прикладываем усилие для движения газа относительно поверхности, чем больше динамическое давление , тем меньше статическое давление , поскольку их сумма – полное давление газа 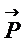, остаётся неизменным.

Если в уравнение (1) поставить значение динамического давления , и переставить местами и , то получим:

 

(2)

где и соответственно, плотность газа и квадрат скорости газа вдоль поверхности. Это уравнение можно назвать основным уравнением аэрогидродинамики, поскольку оно составлено относительно всех трёх величин - статического давления, динамического давления и полного давления газа (жидкости), а формулу (2) - формулой основного закона аэродинамики.

Если сравнить уравнение (2) с уравнением Бернулли (3), то увидим удивительное сходство:

 

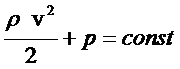(3)

 

 

Закон Бернулли

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

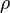— плотность жидкости,

— скорость потока,

— высота, на которой находится рассматриваемый элемент жидкости,

— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

— ускорение свободного падения.

В научной литературе закон Бернулли, как правило, называется уравнением Бернулли ^[1](не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли ^[2][3] или интегралом Бернулли ^[4][5].

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»^[6]).

Соотношение, близкое^[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы и уравнение Бернулли принимает вид: .

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности : .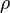

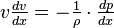Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового , статического и динамического давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.

Содержание 1 Одно из применений 2 Для сжимаемого идеального газа 3 Термодинамика закона Бернулли 4 Практические следствия 5 Приложение 6 См. также 7 Литература 8 Ссылки 9 Примечания

Одно из применений

Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.

Закон Бернулли позволяет объяснить эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем на участке трубы большего диаметра, в результате чего наблюдается разница высот столбов жидкости ; бо́льшая часть этого перепада давлений обусловлена изменением скорости течения жидкости, и может быть вычислена по уравнению Бернулли

Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:

,

где

— атмосферное давление,

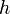— высота столба жидкости в сосуде,

— скорость истечения жидкости,

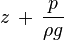— гидростатический напор (сумма геометрического напора z и пьезометрической высоты ).

Отсюда: . Это — формула Торричелли. Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты .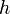

Часто уравнение Бернулли записывается в виде:

где

— гидродинамический напор,

— скоростной напор.

Поделиться:

Воспользуйтесь поиском по сайту: