 |
Дифференциальное уравнение Эйлера.
|
|
|
|
Гидродинамика.
Гидродинамика изучает движение жидкостей и газов. Различают внешнюю и внутреннюю задачу гидродинамики.
· Внутренняя: связана с движения жидкости внутри труб;
· Внешняя: связана с изучением закономерностей обтекания жидкостей или газов различных тел.
Движущей силой является разность давлений создаваемая насосами.
Основные характеристики движения жидкости.
1. Скорость и расход.
Количество жидкости, протекающее через поперечное сечение потока в единицу времени, называется расходом. Различают объемный и массовый расход.
По сечению трубы скорость движения жидкости не одинакова.
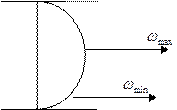
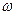- отношение объемного расхода жидкости к площади поперечного сечения.
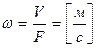
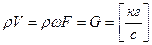- массовый расход
2. Эквивалентный диаметр.
При движении жидкости в трубах некруглого сечения вместо диаметра используют величину эквивалентного диаметра.
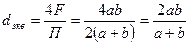
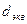- диаметр динамического круглого сечения у которого отношение площади поперечного сечения к смоченному периметру такое же как и трубопровода круглого сечения.
3. Потоки
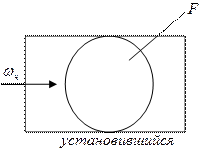
· Установившийся.
Движение жидкости является установившимся или стационарным, если скорость частиц жидкости и упругие параметры(плотность, температура, давление) не изменяются во времени для каждого сечения потока.
· Не установившийся.
Все выше перечисленные величины зависят не только от координат но и от времени.
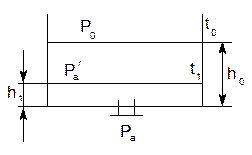
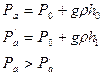
4. Режимы движения жидкости.
· Ламинарный режим движения жидкости наблюдается при малых скоростях или высокой вязкости жидкости при этом жидкость движется параллельными слоями, не смешиваясь друг с другом.
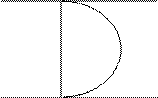
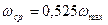
· Турбулентный режим движения жидкости характеризуется вихревым движением потока, в котором присутствуют пульсации и завихрения.
|
|
|
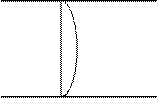
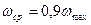
Создание турбулентного режима требует больших затрат энергии по сравнению с ламинарным.
Опыты Рейнольдса показали, что переход от ламинарного режима к турбулентному тем легче чем выше массовая скорость жидкости и диаметр трубы и чем меньше динамическая вязкость жидкости.
Критерий Рейнольдса.
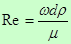- определяем режим движения жидкости
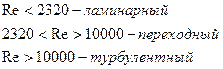Режим движения жидкости по аппаратам оказывает первостепенное влеяние па процессы тепло и массопередачи, для эффективности необходим турбулентный режим движения. Около стенки всегда будет ламинарный режим движения жидкости.
Уравнение неразрывности потока.
Уравнение неразрывности потока – это уравнение устанавливает общую зависимость между скоростями в потоке жидкости, для которого наблюдается условие неразрывности движения.
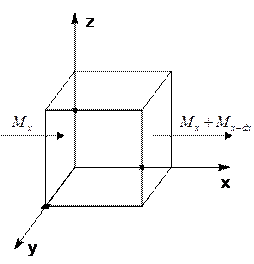
Рассмотрим движение массы жидкости по всем трем направлениям.
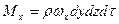[кг]
Количество вещества зашедшее по оси Х:
Количество вещества зашедшее по оси Y:
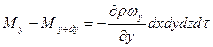
Количество вещества зашедшее по оси Z:
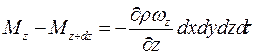
Общее накопление массы вещества в единице объема состовляет:
1) 
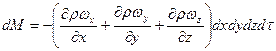
В соответствии с законом сохранения массы: сумма накоплений в единице объема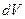 
должна быть равна убыли массы в объеме 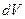за время 
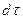, т.е.
2) 
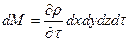
1 = 2
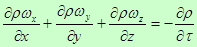
Полученное выражение представляет собой дифференциальное уравнение неразрывности потока для неустановившегося движения.
Дифференциальное уравнение неразрывности потока для неустановившегося движения.
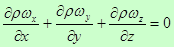
Система: «труба по которой движется материальный поток».
Ориентация по оси Х:
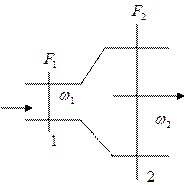
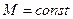
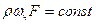- массовый расход
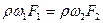
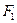
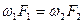
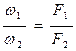
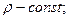
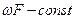
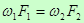- уравнение расхода.
Это уравнение позволяет при заданном режиме движения жидкости рассчитать площадь поперечного сечения(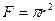
).
Дифференциальное уравнение Эйлера.
|
|
|
Рассмотрим установившийся поток идеальной жидкости, движущейся без трения, через элементарный объем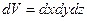 
.
Рассмотрим проекции всех сил на соответствующие оси:
Х: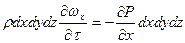 
Y: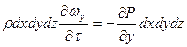 
Z: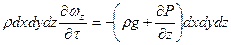 
Согласно основному закону динамики сумма проекций сил, действующих на элементарный объем жидкости по всем трем направлениям, равна произведению массы на ускорение:
Х: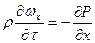 
Y: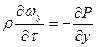 
Z: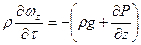 
Полученная система уравнений представляет собой дифференциальное уравнение движения идеальной жидкости для установившегося потока.
|
|
|
