 |
Уравнение прямой в пространстве по точке и
|
|
|
|
направляющему вектору.
Возьмем произвольную прямую и вектор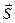 
(m, n, p), параллельный данной прямой. Вектор 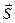называется направляющим вектором прямой.
На прямой возьмем две произвольные точки М0(x0, y0, z0) и M(x, y, z).
z
M1
M0
0 y
x
Обозначим радиус- векторы этих точек как и 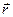, очевидно, что - = 
.
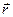Т.к. векторы и 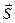коллинеарны, то верно соотношение = 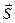t, где t – некоторый параметр.
Итого, можно записать: 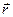= + 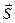t.
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
Это векторное уравнение может быть представлено в координатной форме:
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
.
Определение. Направляющими косинусами прямой называются направляющие косинусы вектора 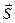, которые могут быть вычислены по формулам:
; 
.
Отсюда получим: m: n: p = cosa: cosb: cosg.
Числа m, n, p называются угловыми коэффициентами прямой. Т.к. 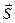- ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
Уравнение прямой в пространстве, проходящей
через две точки.
Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) и M2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
.
Кроме того, для точки М1 можно записать:
.
Решая совместно эти уравнения, получим:
.
Это уравнение прямой, проходящей через две точки в пространстве.
Общие уравнения прямой в пространстве.
|
|
|
Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.
Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:
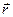× + D = 0, где
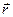- нормаль плоскости; - радиус- вектор произвольной точки плоскости.
Пусть в пространстве заданы две плоскости: 
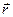× + D1 = 0 и 
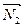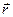× + D2 = 0, векторы нормали имеют координаты: (A1, B1, C1), 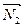(A2, B2, C2); 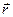(x, y, z).
Тогда общие уравнения прямой в векторной форме:
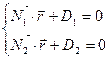
Общие уравнения прямой в координатной форме:
Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.
Для этого надо найти произвольную точку прямой и числа m, n, p.
При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.
Пример. Найти каноническое уравнение, если прямая задана в виде:
Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.
, т.е. А(0, 2, 1).
Находим компоненты направляющего вектора прямой.
Тогда канонические уравнения прямой:
Пример. Привести к каноническому виду уравнение прямой, заданное в виде:
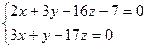
Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:
;
2x – 9x – 7 = 0;
x = -1; y = 3;
Получаем: A(-1; 3; 0).
Направляющий вектор прямой: 
.
Итого: 
Угол между плоскостями.
 |
j1
j 0
Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j1 соотношением: j = j1 или j = 1800 - j1, т.е.
cosj = ±cosj1.
Определим угол j1. Известно, что плоскости могут быть заданы соотношениями:
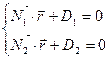, где
(A1, B1, C1), 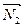(A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения:
.
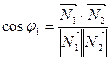Таким образом, угол между плоскостями находится по формуле:
|
|
|
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
|
|
|
