Давление жидкости. Задачи. Домашнее задание: №№ 1-7.

Задача 1. В цилиндрический стакан налита жидкость плотностью ρ. Высота уровня жидкости (над дном стакана) равна h. Разделив вес жидкости на площадь дна стакана, выведите формулу гидростатического давления столба жидкости p = ρgh.

Задача 2. При измерении давления в озере были обнаружены следующие результаты. Давление на расстоянии h = 5 м от дна в n = 3 раза больше давления на глубине h = 5 м. Найти глубину озера. Атмосферным давлением пренебречь.

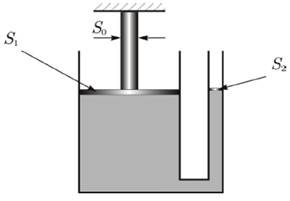
Задача 3. У гидравлического пресса большой поршень имеет площадь S₁ = 80 см², а малый поршень — площадь S₂ = 25 мм² (левый рисунок). На малый поршень пресса действуют направленной вертикально вниз силой F = 0,1 Н. При этом большой поршень давит на вертикально установленный металлический цилиндр, площадь горизонтального основания которого S₀ = 0,8 см² (верхнее основание цилиндра упирается в потолок). Какое давление оказывает большой поршень на нижнее основание цилиндра? Силой тяжести можно пренебречь.

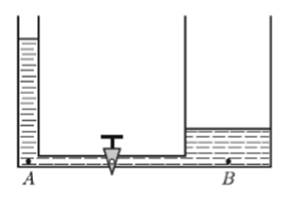
Задача 4. В сосуды, соединённые трубкой с краном, налита вода (см. правый рисунок). Гидростатическое давление в точках A и B равно p_A = 4 кПа и p_B = 1 кПа соответственно, площади поперечного сечения левого и правого сосудов составляют S_A = 3 дм² и S_B = 6 дм² соответственно. Какое гидростатическое давление установится в точках A и B, если открыть кран?

Задача 5. «Но как Вы догадались, Холмс, что это принадлежит полковнику Морану?», — воскликнул удивлённый Ватсон, разглядывая, как Холмс достаёт из сосуда с жидкостью плавающий кубик. «Элементарно, Ватсон!» — опять произнес Шерлок Холмс, подытоживая очередное запутанное дело. «Вот главная улика. Этот кубик весьма лёгок, а его ребро составляет треть фута. Вы заметили, Ватсон, на какую глубину был погружён кубик в жидкость? Нет? Это самое важное, Ватсон! Если не учитывать атмосферное давление, то можно получить очень интересный результат: сила давления жидкости на дно этого плавающего кубика в 5 раз больше, чем средняя сила давления этой жидкости на любую из его боковых стенок. Такой кубик мог быть только у одного человека — человека, вернувшегося из Индии». Определите, на какую глубину погружался в жидкость таинственный кубик. Ответ выразите в сантиметрах. 1 фут = 0,3 м.

Задача 6. В цилиндрическую мензурку, частично заполненную маслом, на тонкой нити полностью погрузили слиток золота. Гидростатическое давление около дна мензурки увеличилось на 50%. Во сколько раз масса золота больше массы масла? Плотность масла 900 кг/м³, плотность золота 19,3 г/см³. Масло через край не выливалось. Ответ округлить до десятых. Атмосферное давление не учитывать.

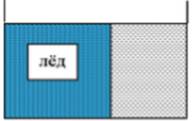
Задача 7. В прямоугольной кювете с солёной водой 0,28 часть объёма была занята пресным льдом, примороженным к стенкам и дну, причём уровень воды и льда совпадал (см. рисунок слева). После того как лёд растаял, гидростатическое давление около дна изменилось. Определите: на сколько процентов? Атмосферное давление не учитывать. Начальная плотность солёной воды 1050 кг/м³, плотность льда 900 кг/м³. Ответ округлите до целых.

Задача 8. Школьнику поручили полить сад на даче. Чтобы не таскать воду в лейке, он проложил толстый шланг через грядки на огороде так, как показано на рисунке справа, продул шланг, вставил в него небольшую воронку и начал медленно наливать в неё воду. Через некоторое время воронка заполнилась, вода в ней перестала опускаться, но из другого конца шланга не полилась. Тогда школьник поднял воронку выше и налил в неё ещё воды. Приблизительно до какой высоты H над землёй ему надо поднять воронку с водой, чтобы она начала вытекать из шланга? Высота каждой грядки h = 40 см, число грядок n = 5.

Решение задачи 8:

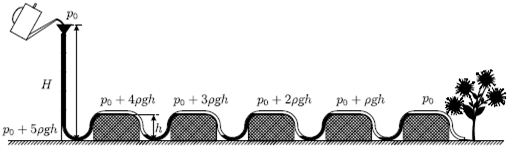
При медленном наливании воды в шланг она доходит до гребня первой грядки, стекает по шлангу вниз и начинает заполнять следующий его отрезок — до гребня второй грядки. При этом в куске шланга, спускающемся с первой грядки, остаётся воздушная пробка, запертая с двух сторон водой. При дальнейшем наливании воды в шланг и постепенном подъёме воронки процесс повторяется, образуются новые воздушные пробки, и вода потечёт из конца шланга, только когда дойдёт до гребня последней грядки (см. рисунок).

Если атмосферное давление на выходе из шланга и на уровне воронки равно p ₀, то давление в воздушных пробках при переходе через каждую грядку от конца шланга в сторону воронки возрастает приблизительно на ρgh. Перед первой грядкой оно будет равно, таким образом, p 0+ nρgh, и для его преодоления воронка с водой должна быть поднята на такую высоту H, чтобы давление воды в нижней точке шланга под воронкой было не меньше этой величины: p 0+ ρGH ≥ p 0+ nρgh, или H ≥ nh =2м.

Полученное значение слегка завышено, поскольку с ростом давления объёмы воздушных пробок и перепады высот на грядках немного уменьшаются. Однако полученная высота составляет всего 20% от высоты h 0= p ₀ ρg ≈10м, соответствующей атмосферному давлению p ₀, так что уменьшением объёмов пробок можно пренебречь и считать, что высота воронки над землёй в момент начала вытекания воды из шланга должна составлять примерно H ≈ nh =2м.