Что важно в оформлении решения?

Практикум по математическому анализу

Тема 5. Понятие предела функции. Пределы с неопределенностью вида , и методы их решений.

Понятие предела функции

Пример:

Запись читается как «предел функции при икс, стремящемся к бесконечности».

Что значит ? Это случай, когда неограниченно возрастает, то есть: сначала , потом , потом , затем и так далее до бесконечности.

Что в это время происходит с функцией ?
, , , …

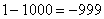Таким образом, если, то функциястремится к минус бесконечности:

Правило: когда дан любой предел, сначала просто пытаемся подставить число (бесконечность) в функцию.

Примеры: (их необходимо осознать и запомнить)

,,

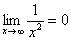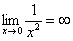
Пределы с неопределенностью вида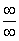и метод их решения

Пример:

Вычислить предел

Согласно правилу, подставить бесконечность в функцию. В числителе получается бесконечность, в знаменателе - также бесконечность. Таким образом, получилась так называемая неопределенность вида 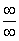. Как решать пределы данного типа?

Сначала смотрим на числитель и находим в старшей степени:

Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим в старшей степени:

Старшая степень знаменателя также равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Д ля того, чтобы раскрыть неопределенность 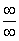необходимо разделить числитель и знаменатель на в старшей степени.

Разделим числитель и знаменатель на

Что важно в оформлении решения?

Во-первых, указать неопределенность, если она есть.

Во-вторых, в пределе помечать, что и куда стремится. Это удобнее сделать так:

 

Пример

Найти предел

 

В числителе и знаменателе найти в старшей степени:

Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно алгоритму, для раскрытия неопределенности поделить числитель и знаменатель на .

 

Разделим числитель и знаменатель на

Пример

Найти предел

 

Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1

Для раскрытия неопределенности необходимо разделить числитель и знаменатель на .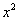

Разделим числитель и знаменатель на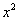

Под записью 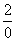подразумевается не деление на ноль (делить на ноль нельзя!!!), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида 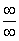у нас может получиться конечное число, ноль или бесконечность.

 

Пределы с неопределенностью видаи метод их решения

Группа следующих пределов чем-то похожа на только что рассмотренные: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Пример 4

Решить предел

 

Сначала попробуем подставить -1 в дробь:

В данном случае получена так называемая неопределенность .

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия необходимо разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.

Итак, решаем предел

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него: .

Далее находим корни:

Таким образом:

Знаменатель уже является простейшим множителем, и упростить его никак нельзя.

Можно сократить на :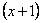

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Пример

Вычислить предел

 

Разложим числитель и знаменатель на множители.

Числитель:
Знаменатель:



,

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Чтобы они не мешали. Главное, потом эти числа не потерять по ходу решения.

! Важно
В ходе решения фрагмент типа встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.

 

Поделиться:

Воспользуйтесь поиском по сайту: