 |
III. Закрепление материала.
|
|
|
|
ГБОУ СПО «ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ»
План урока
Тема урока: Аксиомы стереометрии.
Цели урока:
1. Изучить аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве.
2. Ознакомить учащихся с некоторыми следствиями из аксиом.
3. Сформировать навык применения аксиом стереометрии и их следствий при решении задач.
4. Закрепить усвоение вопросов теории в процессе решения.
Тип урока: урок усвоения новых знаний.
Оборудование урока: чертёжные материалы.
Литература:
Основная: А.В. Погорелов. Геометрия.
Дополнительная: Л.С. Атанасян. Геометрия.
Ход урока:
I. Организационный момент (приветствие, сообщение темы урока, постановка цели урока, сообщение этапов урока, заполнение журнала).
II. Изучение нового материала.
Основными понятиями стереометрии являются точки, прямые и плоскости, которые являются идеализациями объектов реального пространства.
Точка является идеализацией очень маленьких объектов, то есть таких, размерами которых можно пренебречь.
Прямая является идеализацией тонкой натянутой нити, края стола прямоугольной формы. По прямой распространяется луч света.
Плоскость является идеализацией ровной поверхности воды, поверхности стола, доски, зеркала и т.п.
Обсуждаем с учащимися вопрос о том, как точки, прямые и плоскости могут располагаться друг относительно друга.
То, что точка  принадлежит прямой
принадлежит прямой  , обозначается
, обозначается  то, что точка
то, что точка  не принадлежит прямой
не принадлежит прямой  обозначается
обозначается 
Эти обозначения заносим в таблицу 1 и предлагаем учащимся изобразить соответствующие ситуации на рисунке (рис. 1).

Продолжение таблицы 1
| Запись | Чтение |

| Точка  принадлежит прямой принадлежит прямой 
|

| Точка  не принадлежит прямой не принадлежит прямой 
|
| …………………… | ………………………………………………………………….. |
Аналогично, если точка  принадлежит плоскости
принадлежит плоскости  , то пишем
, то пишем  , если точка
, если точка  не принадлежит плоскости
не принадлежит плоскости  , то пишем
, то пишем  . Делаем соответствующие записи в таблицу 1 и предлагаем учащимся изобразить соответствующие ситуации на рисунке (рис. 2).
. Делаем соответствующие записи в таблицу 1 и предлагаем учащимся изобразить соответствующие ситуации на рисунке (рис. 2).
|
|
|
Продолжение таблицы 1
| Запись | Чтение |

| Точка  принадлежит плоскости принадлежит плоскости 
|

| Точка  не принадлежит плоскости не принадлежит плоскости 
|
| …………………… | ………………………………………………………………….. |
Если прямая  лежит в плоскости
лежит в плоскости  , то пишем
, то пишем  , если прямая
, если прямая  пересекает плоскость
пересекает плоскость  в точке
в точке  , то пишем
, то пишем 

Учащимся предлагается модель (рис. 3). Нужно изобразить данную ситуацию и сделать соответствующие записи в таблицу 1.
Продолжение таблицы 1
| Запись | Чтение |

| Прямая  лежит в плоскости лежит в плоскости 
|

| Прямая  не лежит в плоскости не лежит в плоскости 
|

| Прямая  пересекает плоскость пересекает плоскость  в точке в точке 
|
Замечание: Данную модель легко изготовить из куска цветного картона, проткнув его спицей.
 Наконец, рассматриваем вопрос о том, как пересекаются две плоскости. Учащимся предлагается модель (рис. 4). В результате обсуждения делается вывод, что пересечением двух плоскостей является прямая. Нужно изобразить данную ситуацию и сделать соответствующую запись в таблицу 1.
Наконец, рассматриваем вопрос о том, как пересекаются две плоскости. Учащимся предлагается модель (рис. 4). В результате обсуждения делается вывод, что пересечением двух плоскостей является прямая. Нужно изобразить данную ситуацию и сделать соответствующую запись в таблицу 1.
Окончание таблицы 1
| Запись | Чтение |

| Плоскости  и и  пересекаются по прямой пересекаются по прямой 
|
Упражнения.
1. Изобразите точку  , принадлежащую прямой
, принадлежащую прямой  , и точки
, и точки  ей не принадлежащие. Сделайте соответствующие записи.
ей не принадлежащие. Сделайте соответствующие записи.
2. Изобразите точку 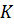 , принадлежащую плоскости
, принадлежащую плоскости  и точку
и точку  , ей не принадлежащую. Сделайте соответствующие записи.
, ей не принадлежащую. Сделайте соответствующие записи.
3. Изобразите две прямые  и
и  ,
,  лежит в плоскости
лежит в плоскости  ,
,  пересекает
пересекает  в точке
в точке  , не принадлежащей прямой
, не принадлежащей прямой  . Сделайте соответствующие записи.
. Сделайте соответствующие записи.
Переходим к введению аксиом. Вспоминаем, что аксиомы геометрии, относящиеся к прямой и плоскости, изучались ранее в курсе планиметрии. «Аксиомы» в переводе с греческого означает «достойная признания». За аксиомы берутся те факты, которые принимаются без доказательства. Остальные факты доказываются с помощью аксиом и носят название теорем, следствий, свойств, признаков и т.д.
|
|
|
В стереометрии изучаются свойства не только плоских, но и пространственных фигур. Так же, как в планиметрии, некоторые свойства принимаются без доказательства и называются аксиомами. Помимо аксиом планиметрии, справедливых для прямых и плоскостей, формулируем аксиомы стереометрии. Вопрос к учащимся: «Какие аксиомы планиметрии вы знаете?» Ответ: I. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
II. Из трёх точек на прямой одна и только одна лежит между двумя другими.
III. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
IV. Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
V. Каждый угол имеет определенную градусную меру, большую нуля. Развёрнутый угол равен  . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
VI. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один.
VII. От полупрямой на содержащей её плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей  , и только один.
, и только один.
VIII. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
IX. На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Введение каждой аксиомы проводим в следующей последовательности:
1) Разъяснение учителем содержания аксиомы и иллюстрация этого свойства на модели.
2) Чтение формулировки аксиомы учащимися (по учебнику, специально приготовленному плакату, через кодоскоп, компьютер и т.п.).
3) Выполнение схематического чертежа.
4) Запись содержания аксиомы с помощью математической символики.
В процессе рассмотрения аксиом с классом заполняем таблицу 2.
|
|
|
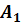 . Через любые три точки, не лежащие на одной прямой, проходит плоскость и при том только одна.
. Через любые три точки, не лежащие на одной прямой, проходит плоскость и при том только одна.
Важно отметить, что если взять не 3, а 4 произвольные точки, то через них может не проходить ни одна плоскость, то есть 4 точки могут не лежать в одной плоскости.
 . Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.
 . Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Говорят, плоскости пересекаются по прямой.
Таблица 2. Аксиомы стереометрии
| Аксиома | Чертёж | Запись |

| 
|  не принадлежат одной прямой не принадлежат одной прямой
  – единственная плоскость – единственная плоскость
|
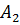
| 
|  все точки прямой все точки прямой  лежат в плоскости лежат в плоскости 
|

| 
| 
|
 Вопросы для учащихся:
Вопросы для учащихся:
1. Сколько плоскостей можно провести через одну прямую?
При ответе на этот вопрос учащимся демонстрируется модель, изображенная на рисунке 5.
2. Точки  и
и  принадлежат плоскости
принадлежат плоскости  . Как расположена прямая
. Как расположена прямая 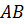 относительно плоскости
относительно плоскости 
3. Возьмем прямую и не принадлежащую ей точку. Можно через них провести плоскость? Почему? Как вы думаете, сколько таких плоскостей можно провести?
4. Даны две пересекающиеся прямые. Можно ли через них провести плоскость? Будет ли она единственной?
После ответов на эти вопросы мы говорим, что эти свойства являются следствиями из аксиом стереометрии, и заполняем следующую таблицу.
Таблица 3. Следствия из аксиом стереометрии
| Следствие | Чертёж | Формулировка |

| 
| Если прямая имеет с плоскостью две общие точки, то она лежит в этой плоскости |

| 
| Через прямую и не принадлежащую ей точку проходит единственная плоскость |

| 
| Через две пересекающиеся прямые проходит единственная плоскость |
Доказательства следствий – первых теорем стереометрии – представляем с подробной записью (дано, требуется доказать).
 Если прямая имеет с плоскостью две общие точки, то она лежит в этой плоскости.
Если прямая имеет с плоскостью две общие точки, то она лежит в этой плоскости.
Дано:  .
.
Доказать:  .
.
Доказательство:
1) Пусть прямая  имеет с плоскостью
имеет с плоскостью  две общие точки -
две общие точки -  и
и  .
.
|
|
|
2) Так как в плоскости  выполняются аксиомы планиметрии, то в этой плоскости через точки
выполняются аксиомы планиметрии, то в этой плоскости через точки  и
и  проходит единственная прямая.
проходит единственная прямая.
3) Если бы она не совпадала с прямой  то мы получили бы две прямые в пространстве, проходящие через две данные точки, а это противоречит аксиоме I. Следовательно, эти прямые совпадают, и значит, прямая
то мы получили бы две прямые в пространстве, проходящие через две данные точки, а это противоречит аксиоме I. Следовательно, эти прямые совпадают, и значит, прямая  лежит в плоскости
лежит в плоскости  .
.
Теорема доказана.
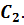 Через прямую и не принадлежащую ей точку проходит единственная плоскость.
Через прямую и не принадлежащую ей точку проходит единственная плоскость.
Дано: 
Доказать: 
Доказательство: Отметим, что теорема содержит два утверждения: 1. О существовании. 2. О единственности плоскости.
а) Рассмотрим прямую  и не лежащую на ней точку
и не лежащую на ней точку  Докажем, что через прямую
Докажем, что через прямую  и точку
и точку  проходит плоскость. Отметим на прямой
проходит плоскость. Отметим на прямой  две точки:
две точки:  и
и  Точки
Точки  не лежат на одной прямой, поэтому согласно аксиоме
не лежат на одной прямой, поэтому согласно аксиоме
 через эти три точки проходит некоторая плоскость
через эти три точки проходит некоторая плоскость  Так как две точки прямой
Так как две точки прямой 
 лежат в плоскости
лежат в плоскости  то по аксиоме
то по аксиоме 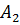 плоскость
плоскость  проходит через прямую
проходит через прямую 
б) Единственность плоскости, проходящей через прямую  и точку
и точку  , следует из того, что любая плоскость, проходящая через прямую
, следует из того, что любая плоскость, проходящая через прямую  и точку
и точку  , проходит через точки
, проходит через точки  . Следовательно, эта плоскость совпадает с плоскостью
. Следовательно, эта плоскость совпадает с плоскостью  , так как по аксиоме
, так как по аксиоме  через точки
через точки  проходит только одна плоскость.
проходит только одна плоскость.
Теорема доказана.
 . Через две пересекающиеся прямые проходит единственная плоскость.
. Через две пересекающиеся прямые проходит единственная плоскость.
Формулировку учащиеся записывают в тетрадь под руководством учителя.
Устно разбирают доказательство, а запись выполняют дома.
Дано: 
Доказать: 
Доказательство: Отметим, что теорема содержит два утверждения: 1. О существовании. 2. О единственности плоскости. Доказательство опирается не на аксиомы, а на следствие 2.
а) Рассмотрим прямые  и
и  , пересекающиеся в точке
, пересекающиеся в точке  . Докажем, что через эти прямые проходит плоскость. Отметим на прямой
. Докажем, что через эти прямые проходит плоскость. Отметим на прямой  какую – нибудь точку
какую – нибудь точку  , отличную от точки
, отличную от точки  , и рассмотрим плоскость
, и рассмотрим плоскость  проходящую через точку
проходящую через точку  и прямую
и прямую  Так как две точки прямой
Так как две точки прямой  лежат в плоскости
лежат в плоскости  , то по аксиоме
, то по аксиоме 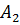 плоскость
плоскость  проходит через прямую
проходит через прямую  Итак, плоскость
Итак, плоскость  проходит через прямые
проходит через прямые 
б) Единственность такой плоскости следует из того, что любая плоскость, проходящая через прямые  , проходит через точку
, проходит через точку  Следовательно, она совпадает с плоскостью
Следовательно, она совпадает с плоскостью  поскольку через точку
поскольку через точку  и прямую
и прямую  проходит только одна плоскость.
проходит только одна плоскость.
Теорема доказана.
III. Закрепление материала.
1. Прочитать формулировки аксиом  -
-  и их следствий
и их следствий  -
-  .
.
2. Решаем задачи:
Задача №1: Точки  не лежат в одной плоскости. Докажите, что прямые
не лежат в одной плоскости. Докажите, что прямые 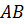 и
и  не пересекаются.
не пересекаются.
Доказательство (методом от противного): Допустим, что 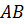 и
и  пересекаются, тогда по следствию
пересекаются, тогда по следствию  через них можно провести плоскость и при том только одну. И в этой плоскости лежат все четыре точки, что противоречит условию задачи. Итак, получили противоречие. Следовательно, прямые
через них можно провести плоскость и при том только одну. И в этой плоскости лежат все четыре точки, что противоречит условию задачи. Итак, получили противоречие. Следовательно, прямые 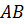 и
и  не пересекаются, что и т.д.
не пересекаются, что и т.д.
|
|
|
 Задача №2: Можно ли через точку пересечения двух данных прямых провести третью прямую, не лежащую с ними в одной плоскости? Объясните ответ.
Задача №2: Можно ли через точку пересечения двух данных прямых провести третью прямую, не лежащую с ними в одной плоскости? Объясните ответ.
Ответ: Можно. Пусть прямые  пересекаются в точке
пересекаются в точке  и лежат в плоскости
и лежат в плоскости  (следствие
(следствие  ). Тогда возьмём точку
). Тогда возьмём точку  вне плоскости
вне плоскости  и рассмотрим прямую
и рассмотрим прямую  . Эта прямая и не принадлежит плоскости
. Эта прямая и не принадлежит плоскости  , а плоскость, содержащая прямые
, а плоскость, содержащая прямые  , единственная (следствие
, единственная (следствие  ). Значит, прямая
). Значит, прямая  - удовлетворяет условию задачи.
- удовлетворяет условию задачи.
Задача №5: Даны две плоскости, пересекающиеся по прямой  и прямая
и прямая  которая лежит в одной из этих плоскостей и пересекает другую. Докажите, что прямые
которая лежит в одной из этих плоскостей и пересекает другую. Докажите, что прямые  и
и  пересекаются.
пересекаются.
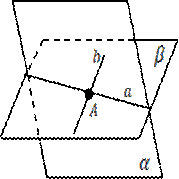 Доказательство: Пусть плоскости
Доказательство: Пусть плоскости  и
и  пересекаются по прямой
пересекаются по прямой  . И прямая
. И прямая  лежит в плоскости
лежит в плоскости  и пересекает плоскость
и пересекает плоскость  в точке
в точке  Точка
Точка  – общая точка двух плоскостей. Тогда по аксиоме
– общая точка двух плоскостей. Тогда по аксиоме  точка
точка  принадлежит прямой
принадлежит прямой  То есть
То есть  и
и  пересекаются. Что и требовалось доказать.
пересекаются. Что и требовалось доказать.
Задача №6: Четыре точки не лежат в одной плоскости. Могут ли какие – нибудь три из них лежать на одной прямой? Объясните ответ.
Ответ: Если какие – нибудь три точки лежат на одной прямой, тогда через эту прямую и четвёртую точку можно провести плоскость (следствие  ). В этой плоскости лежат все четыре точки. А это противоречит условию задачи. Значит, никакие три точки не могут лежать на одной прямой.
). В этой плоскости лежат все четыре точки. А это противоречит условию задачи. Значит, никакие три точки не могут лежать на одной прямой.
Задача №10: Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.
 Доказательство: Проведем плоскость
Доказательство: Проведем плоскость  через данную прямую
через данную прямую  и точку
и точку  (следствие
(следствие  ). Если прямая
). Если прямая  проходит через точку
проходит через точку  и пересекает прямую
и пересекает прямую  в точке
в точке  , то прямая
, то прямая  имеет с плоскостью
имеет с плоскостью  две различные общие точки
две различные общие точки  и
и  , а значит, лежит в полученной плоскости
, а значит, лежит в полученной плоскости  (следствие
(следствие  Что и требовалось доказать.
Что и требовалось доказать.
Задача №11: Докажите, что если прямые 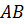 и
и  не лежат в одной плоскости, то прямые
не лежат в одной плоскости, то прямые  и
и  так же не лежат в одной плоскости.
так же не лежат в одной плоскости.
 Доказательство (методом от противного): Допустим, что прямые
Доказательство (методом от противного): Допустим, что прямые  и
и  лежат в одной плоскости
лежат в одной плоскости  , но тогда и
, но тогда и 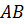 и
и  лежат в той же плоскости
лежат в той же плоскости  так как имеют с ней две различные общие точки. Получаем противоречие с условием задачи. Значит,
так как имеют с ней две различные общие точки. Получаем противоречие с условием задачи. Значит,  и
и  не лежат в одной плоскости. Что и требовалось доказать.
не лежат в одной плоскости. Что и требовалось доказать.
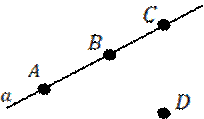 Задача №12: Даны четыре точки, не лежащие в одной плоскости. Сколько можно провести различных плоскостей, проходящих через три из этих точек? Объясните ответ.
Задача №12: Даны четыре точки, не лежащие в одной плоскости. Сколько можно провести различных плоскостей, проходящих через три из этих точек? Объясните ответ.
Ответ: Четыре различных плоскости.
Плоскость задается тремя точками не лежащими на одной прямой (по аксиоме  . Если точки
. Если точки  и
и  не лежат в одной плоскости, то все они и никакие три из них не лежат на одной прямой. Так что имеем четыре возможные тройки точек
не лежат в одной плоскости, то все они и никакие три из них не лежат на одной прямой. Так что имеем четыре возможные тройки точек 
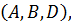 (A, C, D) и
(A, C, D) и  , которые определяют четыре различные плоскости.
, которые определяют четыре различные плоскости.
IV. Итоги урока. Рефлексия. Разбор интересующихся детей вопросов по данной теме. Анализ и успешность достижения цели.
Закончите предложение: «На уроке я узнал…», «Теперь я могу…».
V. Домашнее задание.
1. Повторить аксиомы планиметрии.
2. Выучить аксиомы  -
-  , следствия из аксиом
, следствия из аксиом  -
-  .
.
3. Теорема 3 записать доказательство.
4. Решение задач: стр.10 №3, пункт 1, §1; стр.10 №4, пункт 1, §1.
5. Разобрать задачи: стр.6 №7, пункт 2, §1; стр.7 №9, пункт 3, §1; стр.8 №13, пункт 4, §1.
Решение задач:
 Задача №3: Точки
Задача №3: Точки  лежат на каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.
лежат на каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.
Доказательство: По аксиоме  , так как плоскости
, так как плоскости  и
и  имеют общие точки
имеют общие точки  , то плоскости
, то плоскости  и
и  пересекаются по прямой, которая содержит эти точки. Следовательно, точки
пересекаются по прямой, которая содержит эти точки. Следовательно, точки  принадлежат одной прямой. Что и требовалось доказать.
принадлежат одной прямой. Что и требовалось доказать.
 Задача №4: Даны три различные попарно пересекающиеся плоскости. Докажите, что если две из прямых пересечения этих плоскостей пересекаются, то третья прямая проходит через точку их пересечения.
Задача №4: Даны три различные попарно пересекающиеся плоскости. Докажите, что если две из прямых пересечения этих плоскостей пересекаются, то третья прямая проходит через точку их пересечения.
Доказательство: Допустим, что плоскости  и
и  пересекаются по прямой
пересекаются по прямой  , а плоскости
, а плоскости  и
и  - по прямой
- по прямой  , причем прямые
, причем прямые  и
и  пересекаются в точке
пересекаются в точке  Тогда, по аксиоме
Тогда, по аксиоме  , точка
, точка  принадлежит всем трём плоскостям
принадлежит всем трём плоскостям  , а значит, и третьей прямой
, а значит, и третьей прямой  пересечения плоскостей
пересечения плоскостей  . Что и требовалось доказать.
. Что и требовалось доказать.
Разобранные задачи:
 Задача №7: Докажите, что через прямую можно провести две различные плоскости.
Задача №7: Докажите, что через прямую можно провести две различные плоскости.
Доказательство: Пусть  – данная прямая. По аксиоме I существует точка
– данная прямая. По аксиоме I существует точка  , не лежащая на прямой
, не лежащая на прямой  . По следствию
. По следствию  через прямую
через прямую  и точку
и точку  можно провести плоскость, обозначим её
можно провести плоскость, обозначим её  . По аксиоме (какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей) существует точка
. По аксиоме (какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей) существует точка  , не лежащая в плоскости
, не лежащая в плоскости  Проведем через прямую
Проведем через прямую  и точку
и точку  плоскость
плоскость  Плоскости
Плоскости  и
и  различны, так как точка
различны, так как точка  плоскости
плоскости  не лежит на плоскости
не лежит на плоскости 
Задача №9: Даны две различные прямые, пересекающиеся в точке  Докажите, что все прямые, пересекающие обе данные прямые и не проходящие через точку
Докажите, что все прямые, пересекающие обе данные прямые и не проходящие через точку 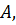 лежат в одной плоскости.
лежат в одной плоскости.
 Доказательство: Проведем через данные прямые
Доказательство: Проведем через данные прямые  плоскость
плоскость  . Это можно сделать по следствию
. Это можно сделать по следствию  . Прямая
. Прямая  , пересекающая данные прямые, имеет с плоскостью
, пересекающая данные прямые, имеет с плоскостью  две общие точки
две общие точки  (точки пересечения с данными прямыми). По аксиоме
(точки пересечения с данными прямыми). По аксиоме 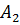 эта прямая должна лежать в плоскости
эта прямая должна лежать в плоскости 
Задача №13: Можно ли провести плоскость через три точки, если эти точки лежат на одной прямой? Объясните ответ.
Ответ: Пусть  – три точки, лежащие на прямой
– три точки, лежащие на прямой  . Возьмем точку
. Возьмем точку  , не лежащую на прямой
, не лежащую на прямой  (аксиома I). Через точки
(аксиома I). Через точки 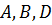 можно провести плоскость (аксиома
можно провести плоскость (аксиома  ). Эта плоскость содержит две точки прямой
). Эта плоскость содержит две точки прямой  – точки
– точки  а значит, содержит и точку
а значит, содержит и точку  этой прямой (аксиома
этой прямой (аксиома 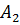 ). Следовательно, через три точки, лежащие на одной прямой, всегда можно провести плоскость.
). Следовательно, через три точки, лежащие на одной прямой, всегда можно провести плоскость.
Подпись преподавателя «___»_____________ 20__год ___________
|
|
|


