 |
Определение и нахождение процента
|
|
|
|
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Методическое пособие составлено в соответствии с Государственным образовательным стандартом среднего профессионального образования
Учебное пособие состоит из нескольких разделов
Каждый раздел имеет краткую теоретическую часть, упражнения для практических занятий. Учитывая профессиональную направленность курса математики, приведены примеры и предложены задачи по дисциплинам фармакологии, педиатрии, основ сестринского дела, акушерства.
Это способствует воспитанию у студентов уверенности в профессиональной значимости изучаемого предмета, студенты видят практическое применение математических методов в медицине и биологии.
По итогам изучения темы студент должен:
знать:
· определение процента;
· меры объема;
· концентрацию растворов;
· понятие пропорций,
уметь:
· составлять и решать пропорции;
· рассчитывать концентрацию растворов;
· получать нужную концентрацию раствора;
· оценивать пропорциональность развития ребенка, используя антропометрические индексы;
· вычислять долженствующую длину, массу, окружность груди и головы ребенка в зависимости от возраста;
· рассчитывать количество молока объемным и калорийным методами, применять вышеизложенные формулы на практике.
Области применения математических методов
в медицине и биологии.
Различные конкретные математические методы применяются к таким областям биологии и медицины, как таксономия, экология, теория эпидемий, генетика, медицинская диагностика и организация медицинской службы.
В том числе методы классификации в применении к задачам биологической систематики и медицинской диагностики, модели генетического сцепления, распространения эпидемии и роста численности популяции, использованию методов исследования операций в организационных вопросах, связанных с медицинским обслуживанием,
|
|
|
Пользуются также математические модели для таких биологических и физиологических явлений, в которых вероятностные аспекты играют подчиненную роль и которые связаны с аппаратом теории управления или эвристического программирования.
Существенно, важен вопрос о том, в каких областях применимы математические методы. Потребность в математическом описании появляется при любой попытке вести обсуждение в точных понятиях и что это касается даже таких сложных областей как искусство и этика. Мы несколько конкретнее рассмотрим области применения математики в биологии и медицине.
До сих пор мы имели в виду главным образом те медицинские исследования, которые требуют более высокого уровня абстракции, чем физика и химия, но тесно связаны с этими последними. Далее мы перейдем к проблемам, связанным с поведением животных и психологией человека, т. е. к использованию прикладных наук для достижения некоторых более общих целей. Эту область довольно расплывчато называют исследованием операций. Пока мы лишь отметим, что речь будет идти о применении научных методов при решении административных и организационных задач, особенно тех, которые непосредственно или косвенно связаны с медициной.
В медицине часто возникают сложные проблемы, связанные с применением лекарственных препаратов, которые еще находятся на стадии испытания. Морально врач обязан предложить своему больному наилучший из существующих препаратов, но фактически он не может сделать выбор. Пока испытание не будет закончено. В этих случаях применение правильно спланированных последовательностей статистических испытаний позволяетсократить время, требуемое для получения окончательных результатов.
|
|
|
Этические проблемы при этом не снимаются, однако такой математический подход несколько облегчает их решение
Простейшее исследование повторяющихся эпидемий вероятностными методами показывает, что такого рода математическое описание позволяет в общих чертах объяснить важное свойство таких эпидемий - периодическое возникновение вспышек примерно одинаковой интенсивности, тогда как детерминистская модель дает ряд затухающих колебаний, что не согласуется с наблюдаемыми явлениями. При желании разработать более детальные, реалистические модели мутаций у бактерий или повторяющихся эпидемий эта информация, полученная с помощью предварительных упрощенных моделей, будет иметь очень большую ценность. В конечном счете, успех всего направления научных исследований определяется возможностями моделей, построенных для объяснения и предсказания реальных наблюдений.
Одно из больших преимуществ, правильно построенной математической модели состоит в том, что она дает довольно точное описание структуры исследуемого процесса. С одной стороны, это позволяет осуществлять ее практическую проверку с помощью соответствующих физических, химических или биологических экспериментов. С другой стороны, математический анализ образом, чтобы в ней с самого начала была предусмотрена соответствующая статистическая обработка данных.
Разумеется, множество глубоких биологических и медицинских исследований было успешно выполнено без особого внимания к статистическим тонкостям. Но во многих случаях планирование эксперимента, предусматривающее достаточное использование статистики, значительно повышает эффективность работы и обеспечивает получение большего объема информации о большем числе факторов при меньшем числе наблюдений. В противном случае эксперимент может оказаться неэффективным и неэкономичным и даже привести к неверным выводам. В этих случаях новые гипотезы, построенные на таких необоснованных выводах, не смогут выдержать проверку временем.
Отсутствием статистического подхода можно в какой-то мере объяснить периодическое появление "модных" препаратов или метод лечения. Очень часто врачи ухватываются за те или иные новые препараты или методы лечения и начинают широко применять только на основании кажущихся благоприятных результатов, полученных на небольших выборках данных и обусловленных чисто случайными колебаниями. По мере того как у медицинского персонала накапливается опыт применения этих препаратов или методов в больших масштабах, выясняется, что возлагавшиеся, на них надежды не оправдываются. Однако для такой проверки требуется очень много времени и она весьма ненадежна и неэкономична; в большинстве случаев этого можно избежать путем правильно спланированных испытаний на самом начальном этапе.
|
|
|
В настоящее время специалисты в области биоматематики настоятельно рекомендуют применять различные статистические методы при проверке гипотез, оценке параметров, планировании экспериментов и обследований, принятии решений или изучении работы сложных систем.
ОПРЕДЕЛЕНИЕ И НАХОЖДЕНИЕ ПРОЦЕНТА
1°. Сотая часть числа называется, одним процентом этого числа, само число соответствует ста процентам. Слово “процент² заменяется символом %.
2°. Пусть дано число  и требуется найти
и требуется найти 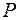 % этого числа. Это будет число
% этого числа. Это будет число  равное
равное


Например: Так, 20% числа 18 дают числа  а,150% числа 18 - число
а,150% числа 18 - число 
При заработной плате 4000 руб. и подоходном налоге 13% налоговые отчисления в бюджет составят  руб.
руб.
3°. Если число  принимается за 100%,то число
принимается за 100%,то число  соответствует
соответствует 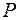 %, причем
%, причем
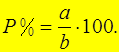

Эта формула позволяет находить какой процент составляет  от
от  .
.
Например: Так, 2 от 4 составляет  , а 12 от 4 составляет
, а 12 от 4 составляет 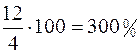 .
.
4°. Если известно, что число  составляет
составляет 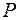 % числа
% числа  , то само число
, то само число  находятся так
находятся так
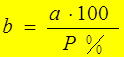

Например: При ставке налога на прибыль 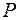 =2 % налоговые отчисления составили 3 млн. руб. Прибыль (до уплаты налога) была равна
=2 % налоговые отчисления составили 3 млн. руб. Прибыль (до уплаты налога) была равна 
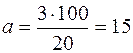 млн. руб.
млн. руб.
МЕРЫ ОБЪЕМА.
1литр (л) = 1 куб. дециметру (дм3)
1 куб. дециметр (дм3) = 1000 куб. сантиметрам (см3)
1 куб. метр (м3) = 1000 000 куб. сантиметрам (см3)
1 куб. метр (м3) = 1000 куб. дециметрам (дм3)
1 мг = 0,001 г
1 г = 1000 мг

ДОЛИ ГРАММА
0,1 г – дециграмм
0,01 – сантиграмм
0,001 – миллиграмм (мг)
0,0001 – децимиллиграмм
|
|
|
0,00001 – сантимиллиграмм
0,000001 – миллимиллиграмм или промилли или микрограмм (мкг)
КОЛИЧЕСТВО МЛ В ЛОЖКЕ
1 ст.л. – 15 мл
1 дес.л. – 10 мл
1 ч.л. – 5 мл
КАПЛИ
1 мл водного раствора – 20 капель
1 мл спиртового раствора – 40 капель
1 мл спиртово-эфирного раствора – 60 капель
|
|
|


