Сдача семестровой работы – последняя лабораторная работа

АТП-121

Акользин №1

1. Определить значение абсолютной температуры воздуха Т на различных высотах и выдать его на печать. Значение высоты в метрах h (0<h<46000)ввести с клавиатуры. На высоте ниже 11000 метров температура вычисляется как Т=288.16-0.0065h. На высоте от 11000 до 25000 метров температура постоянна и равна 216.16. При высоте выше 25000 метров температура определяется по формуле Т=216.16+0.00276098(h-25000).

2.. Выполнить табулирование функции

t принадлежит отрезку [1;5], шаг изменения 0,5; а=2,5

3. Ввести массив В(n) целых чисел. Определить количество k отрицательных элементов. Если K>=A(А задается с клавиатуры), то в исходном массиве найти max среди отрицательных элементов и распечатать его. Если K<A, то сделать соответствующее сообщение.

4.Ввести массив A(n). Все положительные элементы массива переписать в массив В. Если его последний элемент больше 2, то заменить его суммой элементов массива. Массив В распечатать.

Кадыгрова №2

1.Значения переменных X, Y, Z поменять местами так, чтобы они оказались упорядоченными по убыванию.

2.Вычислить h=x³-sin(x+1) в интервале 1≤х≤2.5 с шагом х=0.15. для каждого h выполнить следующее:

Если h≥1.5 вычислить A=h³ -16

Если h<1.5 вычислить A=h³ +1/2Sin h.

Выводить на печать А и h.

3. Ввести массив А(n). Переписать его положительные элементы в массив А1, отрицательные – в массив А2, нулевые элементы игнорировать. Вывести на печать больший из массивов.

4. Ввести массив А(n). Найти максимальный по значению элемент массива и увеличить его в два раза. Все остальные элементы массива уменьшить в 10 раз.

Массив отпечатать.

Калашникова №3

1. Вычислить и напечатать:

Значение x ввести с клавиатуры.

2. Дана функция f(x)= 5/(x+1). Найти количество k значений функции, удовлетворяющих неравенству 1<= f(x)<2. Если k>=2, то отпечатать его, если нет – отпечатать соответствующее сообщение. хÎ[n;m]. Шаг по х=0.2. Учесть, что на 0 делить нельзя.

3. Ввести массив А(n) вещественных чисел. Вычислить квадрат разности между минимальным и максимальным элементами массива и записать его на место предпоследнего элемента. Массив распечатать.

4. Ввести массив А(n). Поменять местами минимумы 1-ой и 2-ой половин массива. Массив отпечатать.

Старостин №4

1. Дан номер месяца — целое число в диапазоне 1–12 (1 — январь, 2 — февраль и т. д.). Вывести название соответствующего времени года («зима», «весна», «лето», «осень»). Решение представить в виде вложенных развилок.

2. Ввести В. Если В<10, выдать на печать 2*В. Если В>=10, вычислить и напечатать значения функции y=x²-x+tg(1/B+x) для значений x, изменяющихся от –3 до 1, с шагом 0,1.

3. Ввести массив целых чисел Х(n). Найти среднее арифметическое значений элементов массива, не принадлежащих интервалу [-2;2]. Если среднее арифметическое значение>2, заменить значения первого и последнего элементов на 1, в ином случае – на 0. Массив распечатать.

4. Ввести массив А(n). Найти сумму положительных элементов массива, исключая при этом те элементы, которые кратны трём. Полученной суммой заменить элементы 2-ой половины массива. Массив отпечатать.

Чемогонов №5

1.Даны три переменные: X, Y, Z. Если их значения упорядочены по возрастанию или убыванию, то удвоить их; в противном случае заменить значение каждой переменной на противоположное.

2. Дана функция f(x)=1/ x⁴. хÎ[n;m]. Шаг по х=0.2. Найти сумму значений функции 0<= f(x)<1. Учесть, что на 0 делить нельзя.

3.Ввести массив К1(n) вещественных чисел. Найти сумму элементов массива. Разделить каждый элемент массива на модуль суммы. Массив распечатать.

4. Ввести массив А(n). Четные элементы массива переписать в массив В, нечетные в С. Вывести на печать тот массив, у которого первый элемент больше.

 

Поцелуйко №6

1.Значения переменных X, Y, Z поменять местами так, чтобы они оказались упорядоченными по возрастанию.

2.Вычислить S= 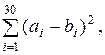где

=

 

=

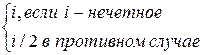
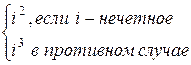
Печатать a, b на каждом шаге, сумму S в конце.

3. Ввести массив А(n). Найти его min и max. Все элементы между минимумом и максимумом возвести в квадрат. Массив отпечатать.

4. Ввести массив А(n). Если сумма его первой трети больше суммы элементов последней трети, то заменить элементы второй трети разностью этих сумм, иначе – нулем. Массив распечатать.

Мигович №7

1.Даны три числа. Вывести вначале наименьшее, а затем наибольшее из данных чисел.

2.На интервале -2.1<=x<=0 с шагом по x=0.01 определить максимальное значение функции

Y=|x|-sin x +0.11.

Результат отпечатать.

3.Ввести массив целых чисел В(n). Найти сумму S положительных элементов. Если S>5, поменять местами значения минимального и максимального элементов. Массив распечатать.

4. Ввести массив А(n). Если в массиве больше положительных элементов, то посчитать сумму первой половины массива, иначе – второй половины. Массив и сумму вывести на печать.

Сидоренко №8

1.Даны целые числа x,y. Если хотя бы одно из них четно, найти min из них. В ином случае – выдать сообщение и нечетности.

2.Дана функция f(x)=1/ x³. хÎ[n;m]. Шаг по х=0.5. Найти сумму S1 положительных значений функции и сумму S2 отрицательных значений функции. Если |S1|<|S2|, отпечатать S1, в ином случае - S2. Учесть, что на 0 делить нельзя.

3.Ввести массив В(n) целых чисел. Подсчитать количество k элементов, значение которых принадлежит интервалу [0;5]. Заменить количеством k элементы массива, значение которых меньше нуля. Массив распечатать

4. Ввести массив А(n). Переписать отрицательные элементы его в новый массив В. Найти сумму элементов, заменить ею последний элемент массива А. Оба массива вывести на печать.

Левченко №9

1.Ввести два числа a и b. Если а>b, то найти с= 1/(a²+b²). Если а=b, выдать об этом сообщение. В противном случае – выяснить, какое из чисел кратно двум и выдать сообщение об этом.

2.Найти среднее арифметическое среди значений функции f(x)= (x+1)², больших 5. На печать выдавать f(x)>5 и среднее арифметическое в конце. хÎ[n;m]. Шаг по х=0.1.

3. Ввести массив А(n) целых чисел. Найти min среди отрицательных элементов, имеющих четное значение. Поставить min на место 2-го, 4-го, 6-го и т.д. элементов. Массив распечатать.

4. Ввести массив А(n). Найти минимальный из положительных элементов матрицы и этим значением заменить все элементы второй половины массива. Массив распечатать.

Привалов №10

1) Составить таблицу значений функций

Y=sin x + cos x

Z= sin x/ cos x – 0.5 x,

x [-2.5;3.5] с шагом по х=0.1. Печатать х, отрицательные у, положительные z на каждом шаге.

 

2) Ввести массив Х(n) целых чисел. Все элементы массива 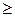3 и кратные 3, заменить на 1; элементы 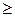3, но не кратные заменить на 0; элементы <3 заменить на (-1). Массив распечатать.

 

3) Ввести массив F(n) вещественных чисел и число Х. Если верно, что min<=X<=max, то массив оставить без изменений, если нет – то умножить все элементы массива на разность между максимумом и минимумом. Массив распечатать.

Русских №11

1) Ввести целое число а. Если а>0, то вычислить максимальное среди значений функции f(x)=e^x/(sin x+cos x) на отрезке [-5;5] с шагом 0.2. В ином случае распечатать все положительные значения функции.

 

2) Ввести массив А(n) вещественных чисел. Если последний элемент массива отрицательный, то найти max на массиве и заменить его значением последний элемент. Массив распечатать. В ином случае сделать сообщение «Массив не изменен».

3) Ввести массив целых чисел Х(n). определить количество элементов, равных первому элементу массива. Если k>0, то найти сумму положительных элементов массива и заменить ею элементы массива, находящиеся по четным адресам. Массив распечатать.

4) Дано x и y. Вычислить z=x²-5xy+tgy, если y=0. Если y=0, выдать сообщение ‘y=0 ’. Если z<10, напечатать b=12y + e^x+5. Если z>=10, вычислить и напечатать c=x² + y² -17.5.

Шмелева №12

1. Даны три действительных числа. Найти и вывести на печать f=min(x+y+z, xyz). Если f<0, то увеличить его в 10 раз и отпечатать, в ином случае – уменьшить в 10 раз и отпечатать.

2. Даны три неравных числа А,В,С. Найти среди них min- минимальное значение и max-максимальное значение. На интервале изменения x от min до max c шагом по х =0.1 вычислить y=1-|x|. Отпечатывать x,y.

3. Ввести массив С(n). Все его четные элементы переписать в массив Х, нечетные – в массив У. Вывести тот массив на печать, размер которого больше.

4. Ввести массив А(n). Преобразовать исходный массив путем сложения его элементов с минимумом средней трети массива. Массив отпечатать.

 

Жуков№13

1. Дано l,m,n. Если l<m, вычислить и отпечатать:

 

t= ln(1+n), при n>2

e^-n, при n<=2.

Если l>=m, то вычислить и отпечатать k=ml² –cos(n).

2. Найти среднее арифметическое среди значений функции f(x)= (x+1)², больших 5. На печать выдавать f(x)>5 и среднее арифметическое в конце. хÎ[n;m]. Шаг по х=0.1.

3. Ввести массив С(n) целых чисел. Подсчитать количество нулевых элементов. Если k составляет больше 50% элементов массива, то все нулевые элементы заменить на 1. Массив распечатать. Иначе дать сообщение – «Массив не преобразован».

4. Ввести массив А(n).Переписать элементы массива, кратные трем, в новый массив В. Найти сумму нового массива и заменить ею предпоследний элемент. Массив отпечатать.

 

Савченко №14

1. Дано целое число K. Вывести строку-описание оценки, соответствующей числу K (1 — «плохо», 2 — «неудовлетворительно», 3 — «удовлетворительно», 4 — «хорошо», 5 — «отлично»). Если K не лежит в диапазоне 1–5, то вывести строку «ошибка». Решение представить в виде вложенных развилок.

 

2. Задано вещественное х. x [n;m]. Шаг по х=0.2.

Составить таблицу значений функции y.

Y=

3. Ввести массивы С1(n) C2(m) и целых чисел. Найти min1 и min2 в каждом из них соответственно. Если min1<min2, распечатать массив С1, иначе – С2.

4. Ввести массив А(n). Найти сумму его чётных элементов. Если она положительна, заменить ею элементы первой половины массива, отрицательна – второй половины. Массив отпечатать.

Слащева №15

1. Вычислить и напечатать:

e^-x, если x>0,

z= 10+ |x|, если x<0,

50, если x=0.

2. Дана функция f(x)=x³-1. хÎ[n;m]. Шаг по х=0.2. Найти сумму отрицательных значений f(x). Отпечатать S.

3. Ввести массив F(n) вещественных чисел. Найти среднее арифметическое среди значений элементов массива. Выдать на печать адреса тех элементов, значения которых превышают значение среднего

4. Ввести массив А(n). Переписать элементы массива А, принадлежащие интервалу [1; 5], в новый массив В. Первый элемент заменить на количество элементов в новом массиве. Массив В распечатать.

Давыдова №16

1. Ввести целые числа x,y. Если x и y больше нуля, то каждое из них заменить на противоположное по знаку. Если больше нуля только х, записать в x, y единицу. В иных случаях – в x, y записать нули. Решать через вложенные развилки. x, y отпечатать.

2. Вычислить h=x³-sin(x+1) в интервале 1≤х≤2.5 с шагом х=0.15. для каждого h выполнить следующее:

Если h≥1.5 вычислить A=h³ -16

Если h<1.5 вычислить A=h³ +1/2Sin h.

Выводить на печать А и h.

3. Ввести массив А(n). Переписать в новый массив все элементы А(n), большие его среднего арифметического. Новый массив распечатать.

4. Ввести массив А(n). Найти минимальный элемент массива среди тех, значения которых кратны трём. Заменить все элементы, предшествующие минимуму, на 0. Массив распечатать.

Дмитриенко №17

1. Даны действительные числа x,y,z. Вычислить min²(x+y+z/2, xyz)+1.

2. Дана функция f(x)=1/ x⁴. хÎ[n;m]. Шаг по х=0.2. Найти сумму значений функции 0<= f(x)<1. Учесть, что на 0 делить нельзя.

3. Ввести массив С(n) целых чисел. Все отрицательные элементы массива заменить нулем, а положительные значения, превышающие некоторое х (задается с клавиатуры), заменить этим значением х. массив распечатать.

4. Ввести массив А(n). Все элементы, находящиеся до максимального переписать в новый массив С. Оба массива распечатать.

Полухин №18

1. Дано x и y. Вычислить z=x²-5xy+tgy, если y<>0. Если y=0, выдать сообщение ‘y=0 ’. Если z<10, напечатать b=12y + e^x+5. Если z>=10, вычислить и напечатать c=x² + y² -17.5.

2. Вычислить значения функции f(x)=1.6x³-1.5. хÎ[n;m]. Шаг по х=0.5. Выдать на печать значения функции f(x) Î[-2;-1].

3. Ввести массив F(n) вещественных чисел. Найти сумму его элементов. Если эта сумма не превышает заданное значение С (задается с клавиатуры), то каждый положительный элемент массива увеличить в два раза. Массив распечатать. Иначе выдать сообщение «Изменений не произошло».

4. Ввести массив А(n).Поменять местами максимумы первой и второй половин массива. Оба массива распечатать..

Шишкин №19

1. Даны целые числа x,y. Если хотя бы одно из них четно, найти min из них. В ином случае – выдать сообщение и нечетности.

2. Дана функция f(x)=1/ x³. хÎ[n;m]. Шаг по х=0.5. Найти сумму S1 положительных значений функции и сумму S2 отрицательных значений функции. Если |S1|<|S2|, отпечатать S1, в ином случае - S2. Учесть, что на 0 делить нельзя.

3. Ввести массив F(n) вещественных чисел. На место каждого отрицательного элемента поставить разность между первым и последним элементами массива. Массив распечатать.

4. Ввести массив А(n). Найти 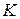– количество чётных элементов в последней трети массива. Если К отлично от нуля, то заменить им элементы первой трети массива, иначе – второй. Массив распечатать до и после преобразования.

Кабдулова №20

1. Вычислить и напечатать:

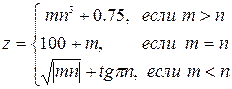
2. Дана функция f(x)= x²-25. хÎ[n;m]. Найти среднее арифметическое SA значений f(x). Шаг по х=0.5. Если SA>=1.5, то отпечатать его, в ином случае – «0».

3. Ввести массив вещественных чисел В(n). Если последний элемент массива отрицательный, то заменить его max значением среди всех положительных элементов. Иначе – сделать сообщение. Массив распечатать.

1. Ввести массив А(n). Найти сумму элементов массива. Если она >0, переписать в массив В положительные элементы, иначе – отрицательные. Сумму и новый массив В распечатать.

Царенко №21

1) Вычислить значения функции y=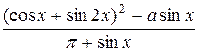

Если x [0;1] с шагом по х=0.1. a вводится с клавиатуры. Напечатать значения x и y.

 

2) Ввести массив В(n) целых чисел (n>=10). Найти сумму последних пяти элементов массива и заменить ею первый элемент массива, если он отрицателен. Массив и сумму распечатать.

 

3) Ввести массив А(n) вещественных чисел. Все положительные элементы переписать в массив А1, найти в нем максимум и поставить его на первое место в А1. Массивы А и А1 распечатать.

 

4) Перераспределить значения переменных X и Y так, чтобы в X оказалось меньшее из этих значений, а в Y — большее.

Крылов №22

1) На интервале x [-5;5] с шагом по х=0.3 рассчитать сумму значений y= , учитывая, что подкоренное выражение не может быть отрицательным. Вычисленные у отпечатать. Вывести значение суммы.

 

2) Ввести массив вещественных чисел В(n). В массиве изменить все знаки отрицательных элементов на положительные. После этого найти максимальный элемент и его номер и распечатать их.

 

3) Ввести массив А(n) вещественных чисел. Найти min и max. Подсчитать сумму элементов, расположенных между максимальным и минимальным. Суммой заменить первый элемент массива. Массив вывести на печать.

 

4) Ввести целые числа x,y. Если x и y больше нуля, то каждое из них заменить на противоположное по знаку. Если больше нуля только х, записать в x, y единицу. В иных случаях – в x, y записать нули. x, y отпечатать.

 

Бланко №23

1) На интервале x [0.5;15] с шагом по х=0.3 рассчитать y= . Среди значений у найти max и вывести его на печать.

 

2) Ввести массив целых чисел Х(n). Найти среднее арифметическое значений элементов массива, не принадлежащих интервалу [-2;2]. Если среднее арифметическое значение>2, заменить значения первого и последнего элементов на 1, в ином случае – на 0. Массив распечатать.

3) Ввести массив F(n) вещественных чисел. Найти среднее арифметическое отрицательных элементов массива. Заменить им все положительные элементы массива. Массив распечатать.

4) Ввести три действительных числа a,b,c. Вычислить k= a²/(b² + c²). Учесть, что b и c не могут быть равны 0. Если k меньше 1, то увеличить его в 10 раз, в противном случае – уменьшить в 10 раз. Распечатать k исходное и вычисленное.

 

 

Симонян №24

1) На интервале изменения x 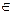[2;5.5] вычислить для каждого х:

Y = x² + |x|; z= cos x -0.3;

Если y>z, вычислить и отпечатать k=y-z.

Иначе вычислить и отпечатать p=y²- .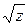

Шаг по х=1.1.

 

2) Ввести массив вещественных чисел В(n). Все элементы массива, которые больше 9, заменить 9, а все элементы, меньшие 5, заменить 5. Остальные элементы оставить без изменения. Массив распечатать.

3) Ввести массив В(n) целых чисел. Вычислить сумму отрицательных элементов. Записать ее модуль на место элемента, стоящего после максимального. Если такого элемента нет, то выдать сообщение. Массив распечатать.

4) Заданы четыре числа. Определить, есть ли среди них хотя бы одна пара равных по величине.

Чебуике №25

1) На отрезке 1.5<=x<=100 с шагом по x=0.5 вычислить y= cos x – 1/x.

Определить S1- сумму отрицательных y;

S2 – сумму положительных y;

S1, S2 отпечатать.

 

2) Ввести массив целых чисел Х(n). Всем элементам, находящимся на нечетных адресах и имеющим нечетное значение, присвоить значение 1. Массив вывести на печать.

 

3) Ввести два массива A(k) и D(m). Найти в каждом из них количества положительных элементов. Вывести на печать тот массив, в котором количество больше.

4) Ввести действительные x,y,z,w. Если x<y<z<w, то каждое число заменить наибольшим из x и y, если x>y>z>w, то каждое число увеличить в два раза, в остальных случаях оставить без изменений. Результат выдать на печать.

 

Прокаев №26

1) Дана функция f(x)=x³. хÎ[n;m].

Найти S1 – сумму положительных значений, S2 – сумму отрицательных значений функции.

На печать выдать все значения функции, S1, S2.

Цикл REPEAT-UNTIL. Шаг цикла=1.

 

2) Ввести массив вещественных чисел В(n). Все элементы массива, которые больше 9, заменить 9, а все элементы, меньшие 5, заменить 5. Остальные элементы оставить без изменения. Массив распечатать.

3) Ввести массив А(n) вещественных чисел. Все положительные элементы массива увеличить на значение предпоследнего элемента массива, а отрицательные – на значение первого элемента. Массив распечатать.

4) Даны действительные числа a,b,c,d. Если a≤b≤c≤d, то каждое число заменить полусуммой трех оставшихся. Если a>b>c>d, то числа оставить без изменения; в противном случае все числа заменяются их квадратами. Результат распечатать.

 

 

Требования к оформлению семестровой работы:

 

Семестровая работа оформляется на листах формата А4 с одной стороны в рукописном виде или электронном виде. Все листы обязательно нумеруются. Первый лист является титульным листом (пример оформления смотри ниже).

Каждое задание должно содержать:

1) условие;

2) один или несколько тестовых примеров, в зависимости от условия задачи;

3) входные данные и выходные данные;

4) математическая модель

5) блок-схемы (основную и пошаговую детализацию);

6) текст программы на языке TurboPascal.

 

Блок-схемы можно оформить в соответствующем пакете (к примеру, MS Visio) или по линейке (обязательно), как и тестовый пример.

Сдача семестровой работы – последняя лабораторная работа

 

Министерство образования и науки Российской Федерации

Федеральное государственное образовательное бюджетное

учреждение высшего образования

Волгоградский государственный технический университет

Кафедра «Вычислительная техника»

 

 

Семестровая работа

 

по дисциплине «Информатика»

 

Вариант №

 

 

Выполнил:

студент группы АТП-121

Иванов И.И.

 

Проверил:

доц. Каф. ВТ Королева И.Ю.

 

Волгоград, 2016 г.

Поделиться:

Воспользуйтесь поиском по сайту: