Определение оптимального решения задачи линейного программирования

После получения опорного решения задачи линейного программи­рования переходим к определению оптимального решения. Оптималь­ным решением (планом) задачи линейного программирования называ­ется такое решение, при котором целевая линейная функция принимает экстремальные (максимальное или минимальное) значения.

Условием оптимальности при отыскании максимального значения целевой функции симплексным методом является отсутствие отрица­тельных коэффициентов в Z-строке симплексной таблицы, т.е. все сво­бодные члены (элементы столбца под 1) в симплекс-таблице неотрица­тельны, в Z-строке (кроме свободного члена) все коэффициенты при пе­ременных также неотрицательны, то полученное решение является опор­ным и оптимальным.

Если же в Z-строке имеется отрицательный коэффициент, то полу­ченное решение не будет оптимальным. Симплекс-метод определения оптимального решения означает переход от одной вершины многогран­ника решений к соседней этого многогранника, в которой значение це­левой функции Z больше или не меньше, чем в исходной вершине.

Для осуществления такого перехода выполняется шаг модифициро­ванного жорданова исключения. В симплексной таблице разрешающий (ведущий) столбец определяется вводимой переменной, а разрешающую (ведущую) строку предполагают исключаемой переменной. Элемент, на­ходящийся на пересечении разрешающей строки и разрешающего столб­ца, называют разрешающим (ведущим).

Если в Z-строке симплексной таблицы имеется несколько отрица­тельных коэффициентов, то в качестве разрешающего столбца выбираем наибольший по модулю отрицательный элемент этой строки.

В разрешающем столбце выбираем все положительные коэффициенты и делим на них соответствующие свободные члены. Из полученных отно­шений принимаем наименьшее и соответствующую строку считаем разре­шающей. После шага модифицированного жорданова исключения с соот­ветствующим разрешающим элементом знак у коэффициента Z-строки изменяйся на противоположный. Если все коэффициенты этой строки ока­жутся неотрицательными, то план будет оптимальным и задача решена.

Если же в разрешающем столбце (столбец с отрицательным коэффи­циентом Z-строки) нет положительных коэффициентов, то целевая функция не ограничена сверху и оптимального решения не существует.

Пример 4.3

Для реализации трех видов товаров предприятие располагает тремя видами ресурсов b₁ = 180, b₂ = 50 и b₃ = 40. Для продажи первой группы товаров на одну тысячу рублей товарооборота расходуется ресурсов пер­вого вида в количестве а₁₁ = 3 единицы, ресурсов второго вида а₂₁ = 2 еди­ницы и третьего а₃₁ = 2 единицы. Для продажи второй и третьей групп товаров на 1 тысячу рублей товарооборота расходуется соответственно:

a_2l = 6 единиц, a_l3 = 4 единицы, а₂₂ = 1 единицу, a₂₃ = 2 единицы, а₃₂ =3 еди­ницы, а₃₃ = 1 единицу.

Прибыль, полученная от продажи трех групп товаров на единицу то­варооборота, составляет: с₁ = 6, с₂ = 5 и с₃ = 5.

Определить максимальную прибыль предприятия.

Математическая модель задачи имеет вид:

(4.20)

 

при ограничениях-неравенствах:

(4.21)

 

и условиях:

(4.22)

 

Решение

1. Вводим зависимые переменные y_i ≥ 0 удовлетворяющие условиям:

и перепишем ограничения (4.16) и целевую функцию Z (4.20) в виде:

(4.23)

 

(4.24)

2. Составляем симплексную табл. №1, включая в нее независимые пере­менные -x_1, -x₂,-х₃, на верху таблицы, зависимые переменные y₁,y_2,у₃ и целевую функцию Z, записывая в левом столбце таблицы с соот­ветствующими знаками у коэффициентов - a_ik. Ограничения на знак в таблицу не включаем.

Первоначальный план (исходное решение) является опорным, так как при х₁ = х₂ = х₃ = 0 (все переменные, расположенные на верху таблицы, равны нулю) и зависимые переменные у₁ = 180, у₂ = 50, у_ъ = 40 удов­летворяют условиям у_i ≥ 0.

3. Определяем оптимальное (максимальное) решение задачи линейного программирования. Находим разрешающий элемент a_rs. В качестве разрешающего выбираем столбец, содержащий наиболь­ший отрицательный по абсолютной величине коэффициент Z-строки, равный «-6». В табл. № 1 указано вертикальной стрелкой. Разрешающую строку определяем из условия min

Такой строкой будет третья (указана горизонтальной стрелкой). Сле­довательно a_rs = а₃₁ = 2.

Выполним шаг модифицированного жорданова исключения с раз­решающим элементом а₃₁ = 2, отмечено квадратиком. Получим табл. №2 в виде:

Разрешающий элемент а₃₁ = 2, заменяем обратной величиной, рав­ной 1/2. Все остальные элементы разрешающего столбца делим на «-2», получаем

Остальные элементы разрешающей строки делим на 2 и получаем:

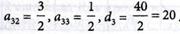
Все элементы табл. №2 получаем, вычисляя по правилу «прямо­угольника».

Вычисления элементов таблицы запишем по строкам:

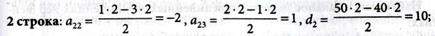
Решение, представленное табл. № 2, не является оптимальным, так как в Z-строке имеется отрицательный коэффициент, равный -2. Выпол­ним шаг модифицированного жорданова исключения с разрешающим элементом а₂₃ = 1 (третий столбец — разрешающий, а строка определена из условия min

и получим табл. № 3 в виде:

Вычисления для заполнения табл. № 3 выполняем, начиная с разре­шающих строки и столбца, а затем определяем элементы столбца сво­бодных членов и Z-строки. Так как свободные члены и коэффициенты Z-строки неотрицательны, то решение является оптимальным. Осталь­ные элементы симплекс-таблицы можно не вычислять.

Решение задачи выписываем из табл. № 3:

у₃ = х₂ = у₂ = 0, так как все переменные, расположенные на верху табли­цы равны нулю. Тогда переменные, находящиеся в левом столбце таблицы равны соответствующим значениям свободных членов (элементы в столбце под «1»), то есть

 

Проверка.

Ответ:

 

12	Поделиться:

Воспользуйтесь поиском по сайту: