 |
Метод пошаговой детализации
|
|
|
|
Занияе 4. Разработка программ. Метод пошаговой детализации. Представление о структурном и модульном программировании
Метод пошаговой детализации
Предыдущие три раздела были посвящены материалу, который вам, хотя бы отчасти, уже знаком. М-функции фактически являются подпрограммами, знакомыми, например, по Фортрану. Операторы цикла и условные операторы примерно одинаково выглядят в любом языке программирования. Сложность заключается не в том, чтобы выучить эти конструкции языка программирования – их не так много. Гораздо труднее научиться составлять из этих конструкций работающие программы.
Обычная ошибка начинающего – сразу хвататься за написание операторов программы. Между тем, как и в любом виде деятельности, успех любой работы зависит от того, насколько хорошо она спланирована. Итак, первый вывод – прежде чем начать писать текст программы, эту программу следует спланировать.
Один из лучших методов планирования программ – метод пошаговой детализации – рассматривается ниже. В качестве задачи, на примере которой будет разобран этот способ, рассмотрим решение системы линейных уравнений по методу Гаусса. Если вы не очень твердо помните этот метод, перед чтением последующего материала перечитайте соответствующие параграфы методического пособия теоретической части курса.
Прежде всего, надо четко сформулировать поставленную задачу. Берете чистый лист бумаги и пишете вверху:
Решить систему n линейных уравнений Ax=b.
Задача сформулирована четко, но как ее решать, по-прежнему непонятно. Попытаемся разбить эту задачу на несколько подзадач. В методе Гаусса напрашивается следующее разбиение:
|
|
|
Решить систему n линейных уравнений Ax=b.
- Привести систему к треугольному виду
- Решить треугольную систему
Между строчками на листе бумаги оставляйте достаточно большие промежутки. Теперь наша задача разбита на две подзадачи, каждая из них проще исходной. Но пока что и эти задачи слишком сложны для того, чтобы сразу записать текст программы.
Сосредоточимся на первой из них и попробуем и ее разбить на более простые подзадачи:
Решить систему n линейных уравнений Ax=b.
- Привести систему к треугольному виду
Для i=1,2,…,n-1
Исключить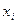 
из уравнений i+1,i+2,…,n
Конец цикла по i
- Решить треугольную систему
Задача: Исключить 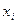из уравнений i+1,i+2,…,n уже значительно проще задач, с которых мы начинали, но, пожалуй, неплохо будет продолжить детализацию:
Решить систему n линейных уравнений Ax=b.
- Привести систему к треугольному виду
Для i=1,2,…,n-1
Исключить 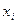из уравнений i+1,i+2,…,n:
Для j=i+1,…,n
Исключить 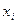из j-го уравнения
Конец цикла по j
Конец цикла по i
- Решить треугольную систему
На этом детализацию можно было бы уже закончить, но если задача «Исключить 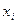из j-го уравнения» вам кажется не совсем понятной, то и ее следует разбить на более элементарные шаги:
Решить систему n линейных уравнений Ax=b.
- Привести систему к треугольному виду
Для i=1,2,…,n-1
Исключить 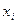из уравнений i+1,i+2,…,n:
Для j=i+1,…,n
Исключить 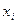из j-го уравнения:
Вычислить коэффициент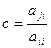 
Вычесть из j-й строки i-ю строку, умноженную на c
Вычесть из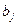 
число 
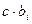
Конец цикла по j
Конец цикла по i
- Решить треугольную систему
Теперь первая подзадача детализирована настолько подробно, что написать операторы MATLAB’а, соответствующие каждой строчке составленного плана, не составит труда.
Аналогичным образом детализируется вторая подзадача. Окончательный план программы может выглядеть примерно так:
- Привести систему к треугольному виду
Для i=1,2,…,n-1
|
|
|
Исключить 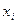из уравнений i+1,i+2,…,n:
Для j=i+1,…,n
Исключить 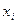из j-го уравнения:
Вычислить коэффициент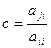
Вычесть из j-й строки i-ю строку, умноженную на c
Вычесть из 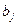число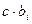
Конец цикла по j
Конец цикла по i
- Решить треугольную систему
Найти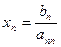 
Для i=n-1,n-2,…,1
Вычислить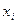
Конец цикла по i
Конечным результатом детализации должен быть совершенно ясный для вас план программы, составленный на обычном разговорном языке. Это необходимо. Если вы сами не представляете ясно, как должен выполняться каждый шаг решения, то вы тем более не сможете объяснить это машине (составить программу).
Насколько подробной должна быть детализация? Это зависит только от вас. Как только вы почувствовали, что четко представляете, как перевести каждую строчку вашего плана на язык MATLAB’а, – заканчивайте детализацию и переходите к написанию программы.
Важное замечание. Автор этого пособия учился программировать, когда главным носителем информации были перфокарты. Поэтому планировать программу неизбежно приходилось на бумаге. В наше время, когда даже писатели-беллетристы и поэты зачастую не притрагиваются к пишущим инструментам и бумаге, а предпочитают пользоваться клавиатурой и монитором, такой подход выглядит архаизмом. И действительно, все планирование можно выполнить на экране.
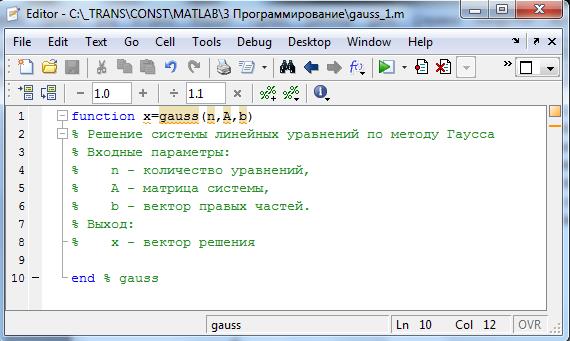
Откройте встроенный редактор MATLAB’а. Сначала следует записать заголовок функции и заголовочные комментарии:
 |
После этого пошаговую детализацию выполняете непосредственно в окне редактора, используя операторы комментариев
Теперь, когда детализация завершена, каждую строчку плана следует заменить операторами MATLAB’а. Строки, содержащие пункты плана, можно при этом не уничтожать. В этом случае они будут играть роль поясняющих комментариев.
В результате файл с программой будет иметь примерно такой вид:
function x=gauss(n,A,b)
% Решение системы линейных уравнений по методу Гаусса
% Входные параметры:
% n - количество уравнений,
% A - матрица системы,
% b - вектор правых частей.
% Выход:
% x - вектор решения
% 1. Приведение системы к треугольному виду
for i=1:n-1 % Для i=1,2,...,n-1
for j=i+1:n % Для j=i+1,...,n
c = A(j,i)/A(i,i); % Вычислить коэффициент с=A(j,i)/A(i,i)
|
|
|
A(j,:) = A(j,:) - c*A(i,:);
% Вычесть из j-й строки i-ю строку, умноженную на с
b(j) = b(j) - c*b(i); % Вычесть из b(j) число c*b(i)
end % Конец цикла по j
end % Конец цикла по i
% 2. Решение треугольной системы
x(n) = b(n)/A(n,n); % Найти x(n) = b(n)/A(n,n)
for i=n-1:-1:1 % Для i=n-1,n-2,...,1
x(i) = (b(i) - sum(A(i,i+1:n).*x(i+1:n)))/A(i,i); % Вычислить x(i)
end % Конец цикла по i
Стоит ли оставлять все эти комментарии? Решать, прежде всего, вам – как вам удобнее. Однако приведу некоторые рецепты, проверенные временем:
1) Используйте заголовочные комментарии, в которых указывается назначение программы, описываются входные и выходные параметры;
2) Комментарии должны пояснять операторы программы, а не повторять их;
3) Количество строк комментариев в самом тексте программы бывает различным, но обычно одна строка комментариев приходится на 5-10 строк программы.
Я бы, например, предпочел следующую окончательную редакцию этого программного файла:
function x=gauss(n,A,b)
% Решение системы линейных уравнений по методу Гаусса
% Входные параметры:
% n - количество уравнений,
% A - матрица системы,
% b - вектор правых частей.
% Выход:
% x - вектор решения
% 1. Приведение системы к треугольному виду
for i=1:n-1
for j=i+1:n
c = A(j,i)/A(i,i);
A(j,:) = A(j,:) - c*A(i,:);
b(j) = b(j) - c*b(i);
end
end
% 2. Решение треугольной системы
x(n) = b(n)/A(n,n);
for i=n-1:-1:1
x(i) = (b(i) - sum(A(i,i+1:n).*x(i+1:n)))/A(i,i);
end
Наконец, последнее замечание. Последнее по порядку, но не по значимости (last but not least). Вы, наверное, обратили внимание, что в этом примере строчки начинаются не с одной позиции, а располагаются уступами. Благодаря этому структура программы становится более понятной, хорошо видно, где начинается и где кончается каждый цикл. Также для повышения наглядности бывает полезно вставить пустую строку между отдельными частями программы.
Хотя эти советы могут показаться незначительными мелочами, пренебрегать ими не следует. Затратив совсем немного труда для повышения наглядности программы, вы сэкономите массу времени на ее отладке. Учтите, что все эти рекомендации не выдумка автора, а результат опыта нескольких поколений программистов. Не стоит без необходимости выдумывать свой собственный стиль программирования и стараться быть оригинальным. Оригинальность, конечно, хорошее качество, но… Если большинство людей одевают левый ботинок на левую ногу, а правый на правую, то может быть они в чем-то правы.
|
|
|
|
|
|
12 |
