 |
Бесконечно малые и бесконечно большие функции.
|
|
|
|
ПРЕДЕЛ ФУНКЦИИ
Числовые последовательности. Предел числовой последовательности.
Пусть каждому натуральному числу n поставлено в соответствие действительное число xп. Тогда говорят, что задана последовательность чисел x1, x2, x3, …, xn, ….
Числа x1, x2, x3, …, xn, будем называть элементами (или членами) последовательности, xn – общим членом последовательности.
Сокращенно последовательность обозначается 
.
Определение. Последовательность { xn } называется ограниченной, если она ограничена и сверху и снизу, то есть существуют числа m и M такие, что любой элемент этой последовательности удовлетворяет неравенствам:
В противном случае последовательность { xn } называется неограниченной.
Определение 2. Число a называется пределом числовой последовательности { xn }, если для любого сколь угодно малого ε > 0 найдется число N (номер), зависящее от ε, такое, что для всех натуральных чисел n > N выполняется неравенство:
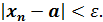
Предел обозначается:
Согласно этому определению в
e – окрестности, то есть в интервале
(а–e, а+e) предельной точки последовательности, находится бесконечное число элементов этой последовательности.
Число а называется пределом последовательности {xn}, если, начиная с некоторого номера N все элементы этой последовательности оказываются в
e – окрестности точки а.
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Предельный переход в неравенствах
Рассмотрим последовательности {xn}, {уn}, {zn}.
Теорема 1.Если
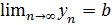и начиная с некоторого номера, выполняется неравенство xn ≤ уn, то а≤ 
.
Теорема 2.
Если
и справедливо неравенство
xn ≤ zn ≤ уn (начиная с некоторого номера), то 
.
|
|
|
ПРЕДЕЛ ФУНКЦИИ
Предел функции в точке и в бесконечности. Основные теоремы о пределах. Бесконечно малые и бесконечно большие функции.
Функцией y=f(x) называется выражение (закон), по которому каждому элементу х соответствует значение y.
Пусть функция y =f (x) определена в некоторой окрестности x0, кроме, может быть, самой точки x0.
Определение. Число A называется пределом функции y =f (x) в точке x0 (или при х →x0), если для любого сколь угодно малого числа ε > 0 найдется такое число
δ > 0, зависящее от e, что для всех х ¹x0, удовлетворяющих неравенству
│ х –x0 │< δ, выполняется неравенство
│ f (x) – А │<ε.
Или кратко:
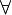ε > 0 
δ > 0,
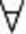x:│ х –x0 │< δ, х ¹x0 => │ f (x) – А │<ε.
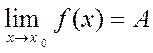
Геометрический смысл предела функции заключается в следующем: число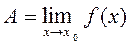 
, если для любой
ε – окрестности точки A найдется такая δ – окрестность точки x0, что для всех х ¹x0 из этой окрестности соответствующие значения функции f (x) лежат в
ε – окрестности точки А.
Рис. 1
Если при х®х0 переменная х принимает лишь значения, меньшие х0 и при этом функция f(x) стремится к некоторому числу А, то говорят, что функция имеет односторонний предел, в данном случае предел слева:
.
Если переменная принимает значения большие х0 при f(x) ® А, то функция имеет предел справа:
.
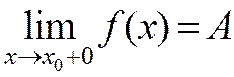Пусть функция y =f (x) определена в промежутке (– 
; + 
).
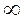Определение. Число A называется пределом функции f (x) при х 
, если для любого числа ε > 0 существует такое число M = M (ε) > 0, что для всех значений x, удовлетворяющих неравенству │ x │ >M, выполняется неравенство │ f (x) – А │< ε.
В этом случае пишут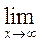 
f (x) = А.
Или кратко:
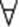ε > 0 
M > 0, 
х:│ x│ > M => │ f (x) – А │<ε.
f (x) = А.
Бесконечно малые и бесконечно большие функции.
Определение. Функция f (x) называется бесконечно малой функцией при х →x0, если 
f (x) = 0. (Б.М.В.)
|
|
|
Определение. Функция f (x) называется бесконечно большой функцией при х →x0, если для любого числа M > 0 существует число δ= δ(М) > 0, что для всех х, удовлетворяющих неравенству
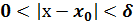, выполняется неравенство │ f (x) │>М.. В этом случае пишут 
f (x) = 
.
Рассмотрим теперь основные свойства б.м.в.,
(которые принято обозначать: 
), определяемые следующими теоремами.
Теорема 1.
|
|
|
