 |
Дз № 1. Определённый интеграл
|
|
|
|
Задача 1. Вычислить площадь фигуры, которая расположена
на плоскости Oxy.
Для каждого номера варианта заданы линии, ограничивающие фигуру.
| Вар. | Уравнения линий, ограничивающих фигуру |

| |
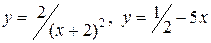
| |

| |
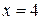 , ,  и касательная к этой линии в точке её пересечения с осью и касательная к этой линии в точке её пересечения с осью 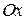
| |

| |

| |

| |
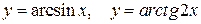
| |
 , , 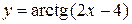 , , 
| |

| |
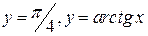 и касательная к этой линии в начале координат и касательная к этой линии в начале координат
| |

| |
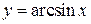 и прямая, проходящая через концы этой линии и прямая, проходящая через концы этой линии
| |

| |
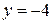 , ,  и касательная к этой линии в точке пересечения ее с осью Ox и касательная к этой линии в точке пересечения ее с осью Ox
| |

| |
| y=arcsinx, касательная к этой линии в начале координат и прямая x=1 | |
| y=arcsinx, y=-arcsin(x-2), y=-π/2 | |
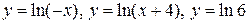
| |

| |
 и прямая, проходящая через начало координат и через точку с абсциссой и прямая, проходящая через начало координат и через точку с абсциссой  на заданной линии. на заданной линии.
| |

| |

| |
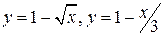
| |
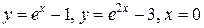
| |

| |
 , ,  и касательная к этой линии в точке пересечения ее с осью Ox и касательная к этой линии в точке пересечения ее с осью Ox
| |

| |

| |

|
Задача 2. Фигура, расположенная на плоскости Oxy, вращается около координатной оси. Вычислить объём полученного тела вращения.
Для каждого номера варианта заданы линии, ограничивающие фигуру, и ось вращения.
| Вар. | Уравнения линий, ограничивающих фигуру | Ось вращения |

| OY | |

| OX | |

| OY | |

| OX | |

| OY | |
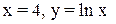 и касательная к этой кривой в точке пересечения ее с осью Ox и касательная к этой кривой в точке пересечения ее с осью Ox
| OY | |

| OY | |

| 
| |
 и ветвь тангенсоиды и ветвь тангенсоиды  , проходящая через начало координат , проходящая через начало координат
| 
| |
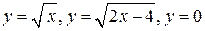
| OY | |

| 
| |
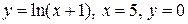
| OY | |
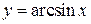 и и 
| 
| |
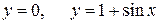 (между двумя соседними точками касания этой линии с осью Ox) (между двумя соседними точками касания этой линии с осью Ox)
| 
| |

| OY | |

|  . .
| |
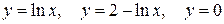
| OY | |
 , при , при  , ,  , при , при 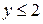 , , 
| OY | |
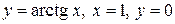
| OY | |

| OY | |

| OY | |

| OY | |
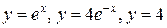
| 
| |
 и касательная к этой кривой в начале координат и касательная к этой кривой в начале координат
| OY | |
 и касательная к этой линии в точке её пересечения с осью Ox и касательная к этой линии в точке её пересечения с осью Ox
| OY | |

| 
| |
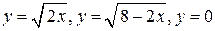
| OY | |
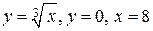
| OY | |

| 
| |
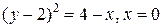
| 
|
Задача 3. Вычислить площадь фигуры.
|
|
|
Для каждого номера варианта задана соответствующая фигура
1. Внутри окружности  и одновременно внутри кардиоиды
и одновременно внутри кардиоиды  ..
..
2. Внутри кардиоиды  и одновременно внутри окружности
и одновременно внутри окружности  .
.
3. Внутри кардиоиды  и одновременно слева от прямой
и одновременно слева от прямой  .
.
4. Внутри окружности  и одновременно внутри кардиоиды
и одновременно внутри кардиоиды 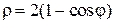
5. Внутри кардиоиды  и одновременно внутри кардиоиды
и одновременно внутри кардиоиды  .
.
6. Внутри правой ветви лемнискаты  и одновременно вне окружности
и одновременно вне окружности  .
.
7. Внутри кардиоиды  и одновременно внутри окружности
и одновременно внутри окружности  .
.
8. Внутри окружности  и одновременно вне лемнискаты
и одновременно вне лемнискаты  .
.
9. Внутри кардиоиды  и одновременно внутри окружности
и одновременно внутри окружности  .
.
10. Внутри кардиоиды  и одновременно вне окружности
и одновременно вне окружности  .
.
11. Внутри окружности  и одновременно вне окружности
и одновременно вне окружности  .
.
12. Внутри окружности  и одновременно внутри кардиоиды
и одновременно внутри кардиоиды 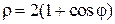 .
.
13. Внутри окружности  и одновременно вне кардиоиды
и одновременно вне кардиоиды  .
.
14. Внутри лемнискаты 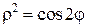 и одновременно внутри окружности
и одновременно внутри окружности  .
.
15. Внутри кардиоиды  и одновременно вне кардиоиды
и одновременно вне кардиоиды  .
.
16. Внутри четырёхлепестковой розы  и одновременно внутри окружности
и одновременно внутри окружности  .
.
17. Внутри окружности  и одновременно вне кардиоиды
и одновременно вне кардиоиды  .
.
18. Внутри окружности r = 3 и одновременно вне кардиоиды 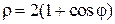 .
.
19. Внутри кардиоиды  и одновременно вне кардиоиды
и одновременно вне кардиоиды  .
.
20. Внутри кардиоиды  и одновременно справа от прямой
и одновременно справа от прямой  .
.
21. Внутри окружности  и одновременно внутри лемнискаты
и одновременно внутри лемнискаты  .
.
22. Внутри окружности  и одновременно вне кардиоиды
и одновременно вне кардиоиды 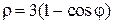 .
.
23. Внутри кардиоиды  и одновременно вне окружности
и одновременно вне окружности  .
.
24. Внутри лемнискаты 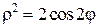 и одновременно вне окружности
и одновременно вне окружности  .
.
25. Внутри кардиоиды  и одновременно внутри окружности
и одновременно внутри окружности 
26. Между двумя лемнискатами 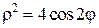 и
и 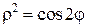 .
.
27. Внутри кардиоиды  и одновременно вне окружности
и одновременно вне окружности  .
.
28. Внутри кардиоиды  и одновременно вне кардиоиды
и одновременно вне кардиоиды  .
.
29. Внутри окружности  и одновременно вне четырёхлепестковой розы
и одновременно вне четырёхлепестковой розы  .
.
30. Внутри окружности  и одновременно вне трёхлепестковой розы
и одновременно вне трёхлепестковой розы  .
.
Задача 4. Вычислить длину дуги кривой.
|
|
|
| Вар. | Уравнение кривой ограничения на переменные |
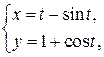 
| |
 , , 
| |
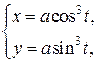 
| |
 , внутри , внутри 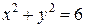
| |
 , ,  , , 
| |
 , вне , вне 
| |

| |
 , , 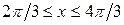
| |
 , , 
| |
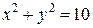 , внутри ветвей гиперболы , внутри ветвей гиперболы 
| |
 , , 
| |
 , , 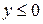
| |
 , , 
| |
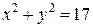 , внутри ветвей гиперболы , внутри ветвей гиперболы 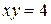
| |
 , внутри окружности , внутри окружности 
| |
 , , 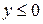
| |
  где где 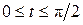
| |
 , , 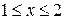
| |
 , , 
| |
 , , 
| |
 , , 
| |
 , внутри , внутри 
| |
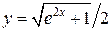 , , 
| |
 , внутри , внутри 
| |
 , , 
| |
 , , 
| |
 , , 
| |
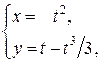 между точками пересечения с осью между точками пересечения с осью 
| |
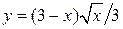 , , 
| |
 , , 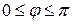
|
Задача 5. Вычислить площадь поверхности, полученной при вращении заданных линий вокруг заданной оси.
| Вар. | Уравнения кривых, ограничения на переменные | Ось вращения |
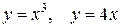 , , 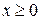
| 
| |
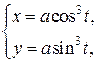 
| 
| |
 , , 
| 
| |

| 
| |
 , , 
| 
| |
 , , 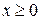
| 
| |
 , , 
| 
| |
 
| 
| |
 , , 
| 
| |
 , , 
| 
| |
 , , 
| 
| |
 , , 
| 
| |
 , ,  . .
| 
| |
 , , 
| 
| |
 , , 
| 
| |
 
| 
| |
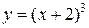 и касательная к этой кривой в точке её пересечения с осью и касательная к этой кривой в точке её пересечения с осью 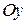 , , 
| 
| |

| 
| |
 , , 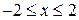
| 
| |

| полярная ось | |

| 
| |
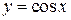 , , 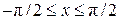
| 
| |
 между точками пересечения с осью между точками пересечения с осью 
| 
| |
 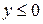 
| 
| |

| 
| |
 , , 
| 
| |

| полярная ось | |
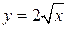 , касательная к этой кривой в точке с абсциссой , касательная к этой кривой в точке с абсциссой  и ось
и ось 
| 
| |
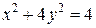
| 
| |
 и касательная к этой кривой в точке её пересечения с осью и касательная к этой кривой в точке её пересечения с осью 
| 
|
Задача 6. Исследовать несобственные интегралы на сходимость.
| Вар. | А) | Б) | В) |

| 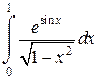
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |
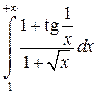
| 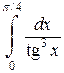
| 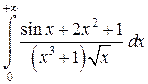
| |

| 
| 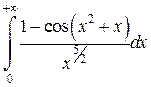
| |

| 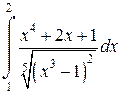
| 
| |
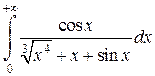
| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 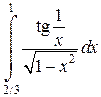
| 
| |

| 
| 
| |

| 
| 
| |

| 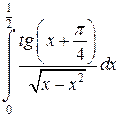
| 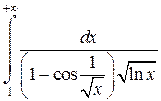
| |

| 
| 
| |

| 
| 
| |

| 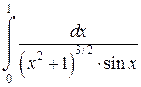
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 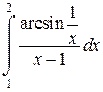
| 
| |

| 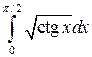
| 
| |
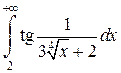
| 
| 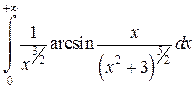
| |

| 
| 
| |
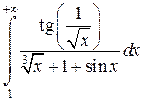
| 
| 
| |

| 
| 
|
|
|
|


