Тестовые задания для контроля конечного уровня знаний

Выберите один правильный ответ

1. УКАЖИТЕ ВИДЫ СВЯЗЕЙ МЕЖДУЯВЛЕНИЯМИ:

1) Корреляционные и регрессионные

2) Функциональные и вспомогательные

3) Корреляционные и функциональные

4) Функциональные и регрессионные

5) Корреляционные и линейные

 

2. СВЯЗЬ СЧИТАЕТСЯ СИЛЬНОЙ, ЕСЛИ ЗНАЧЕНИЕ КОЭФФИЦИЕНТА

КОРРЕЛЯЦИИ:

1) Равно 0

2) В диапазоне от 0 до 0,3

3) В диапазоне от 0,7 до 1

4) В диапазоне от 1 до 2

5) Принимает положительные значения

 

3. ЕСЛИ ОДНОМУ ЗНАЧЕНИЮ ПЕРВОГО ПРИЗНАКА СООТВЕТСТВУЕТ

НЕСКОЛЬКО ЗНАЧЕНИЙ ВТОРОГО – ЭТО СВЯЗЬ:

1) Функциональная

2) Положительная

3) Регрессионная

4) Прямолинейная

5) Корреляционная

 

4. ПРИ ОБРАТНОЙ СВЯЗИ ЗНАЧЕНИЯ ВТОРОГО ПРИЗНАКА ПРИ ИЗМЕНЕНИИ

ПЕРВОГО:

1) Уменьшаются

2) Изменяются прямолинейно

3) Изменяются криволинейно

4) Изменяются в противоположном направлении

5) Изменяются в том же направлении

 

5. УКАЖИТЕ, С КАКОЙ ЦЕЛЬЮ ПРОВОДИТСЯ КОРРЕЛЯЦИОННЫЙ АНАЛИЗ:

1) Выявить и измерить связи между явлениями

2) Оценить статистическую значимость результатов исследования

3) Оценить насколько меняются значения второго признака при изменении первого

4) Измерить степень изменчивости вариационных рядов

5) Определить связь между значениями вариант и их частотами

 

6. КАКИМ МОЖЕТ БЫТЬ ЗНАЧЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ:

1) Близкое к нулю

2) От нуля до единицы (в положительную и отрицательную сторону)

3) Близкое к единице (+1 или -1)

4) Как и значение критерия t Стьюдента,т.е 1,2,3

5) Измеряется в процентах

 

7. КОЭФФИЦИЕНТ РЕГРЕССИИ ВЫЧМСЛЯЕТСЯ С ЦЕЛЬЮ:

1) Количественно измерить связь

2) Оценить как меняются значения второго признака при изменении первого

признака на единицу

3) Оценить регрессивность признака при изменении значений первого на единицу

4) оценить как меняется связь при изменении значений первого признака на единицу

5) Правильный ответ отсутствует

8. ЗАВИСИМОСТЬ НАЗЫВАЕТСЯ ФУНКЦИОНАЛЬНОЙ, ЕСЛИ:

1) одному значению одной переменной величины соответствует множество значений другой

2) одному значению одной переменной величины соответствует одно значение другой

3) одному значению одной переменной величины соответствует два значения другой

4) одному значению одной переменной величины не соответствует ни одно значение другой

.9. КОЭФФИЦИЕНТ ЛИНЕЙНОЙ КОРРЕЛЯЦИИ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ:

1) от до

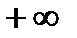
2) от 3 до 1

3) от 2 до 1

4) от до +1

10. МАЛОЙ ВЫБОРКОЙ СЧИТАЕТСЯ ТА СОВОКУПНОСТЬ, В КОТОРОЙ:

1) n меньше или равно 100

2) n меньше или равно 30

3) n меньше или равно 40

4) n близко к 0

11. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ПИРСОНА ОПРЕДЕЛЯЕТ:

1) статистическую значимость различий между переменными

2) степень разнообразия признака в совокупности

3) силу и направление связи между зависимой и независимой переменными

4) долю дисперсии результативного признака объясняемую влиянием независимых переменных

12. УСЛОВИЕМ ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ПИРСОНА ЯВЛЯЕТСЯ:

1) распределение переменных неизвестно

2) нормальное распределение по крайней мере, одной из двух переменных

3) по крайней мере, одна из двух переменных измеряется в ранговой шкале

4) отсутствует нормальное распределение переменных

13. РАНГОВЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ СПИРМЭНА РАССЧИТЫВАЕТСЯ, КОГДА:

1) присутствует нормальное распределение переменных

2) необходимо оценить связь между качественными и количественными признаками

3) необходимо определить статистическую значимость различий между переменными

4) необходимо оценить степень разнообразия признака в совокупности

14. ДЛЯ ИЗОБРАЖЕНИЯ КОРРЕЛЯЦИОННОЙ ЗАВИСИМОСТИ ИСПОЛЬЗУЕТСЯ ГРАФИК:

1) линейный

2) график рассеяния точек

3) радиальный

4) динамический

15. ЕСЛИ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ РАВЕН 1, ТО СВЯЗЬ ЯВЛЯЕТСЯ:

1) сильной, прямой

2) сильной обратной

3) средней, прямой

4) полной (функциональной), прямой

16. СВЯЗЬ МЕЖДУ Y И X МОЖНО ПРИЗНАТЬ БОЛЕЕ СУЩЕСТВЕННОЙ (СИЛЬНОЙ) ПРИ СЛЕДУЮЩЕМ ЗНАЧЕНИИ ЛИНЕЙНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ:

1) r= 0,35

2) r= 0,15

3) r= – 0,57

4) r= 0,46

17. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ИСПОЛЬЗУЕТСЯ ДЛЯ ИЗУЧЕНИЯ:

1) взаимосвязи явлений

2) развития явления во времени

3) структуры явлений

4) статистической значимости различий между явлениями

18. ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ СПИРМЭНА НЕОБХОДИМО:

1) рассчитать сумму данных

2) расположить переменные в порядке чередования

3) возвести переменные в квадрат

4) присвоить переменным в порядке возрастания последовательные ранги (номера 1, 2, 3,.., n)

19.КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ИЗМЕРЯЕТСЯ В:

1) процентах

2) тех же единицах, что и изучаемый признак

3) промилле

4) не имеет единиц измерения

20. ПРИ ИЗУЧЕНИИ ВЛИЯНИЯ ОХВАТА ВАКЦИНАЦИЕЙ ПРОТИВ ДИФТЕРИИ И УРОВНЕМ ЗАБОЛЕВАЕМОСТИ РАССЧИТАН КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ r = – 0,93, ЧТО СВИДЕТЕЛЬСТВУЕТ О НАЛИЧИИ

1) прямой, сильной связи

2) обратной, сильной связи

3) обратной, средней связи

4) прямой, слабой связи

5) связь недостоверная

21. ФОРМУЛА ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ПО МЕТОДУ КВАДРАТОВ (ПИРСОНА):

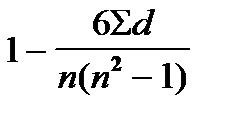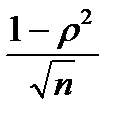1) 2) 3) 4) 5)

22. ФОРМУЛА ДЛЯ ПОЛУЧЕНИЯ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ МЕТОДОМ РАНГОВ (СПИРМЕНА):

1). 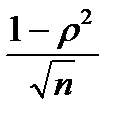2). 3). 4).

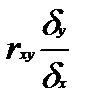
23. КОЭФФИЦИЕНТ СПИРМЕНА ИСПОЛЬЗУЕТСЯ, КОГДА ПРИЗНАКИ ИМЕЮТ ЗНАЧЕНИЕ: 1. Качественное. 2.Количественное. 3. Полуколичественное. 4. Доверительное. 5. Критическое

 

1) верно 1, 4

2) верно 1,2,3

3) верно 3, 5

4) верно 5

Информационный блок

Корреляция - понятие, означающее взаимосвязь между признаками. Согласно диалектико-материалистическому учению о природе и обществе, все явления и процессы, совершающиеся в них, взаимосвязаны и взаимообусловлены. Задача каждой науки - вскрыть и изучить наиболее существенные связи между явлениями и процессами.

В социальной гигиене и организации здравоохранения, в различных разделах медицины и биологии часто приходится проводить статистический анализ связей всевозможных признаков в совокупности. Необходимо уметь изучать особенности этих связей, определять их размеры и характер, а также оценивать их достоверность.

Различают две формы проявления количественных связей между явлениями или процессами: функциональную и корреляционную.

Под функциональной понимают такую связь, при которой любому значению одного из признаков соответствует строго определенное значение другого (радиуса круга соответствует определенная площадь круга, скорость свободно падающего тела определяется величиной ускорения силы тяжести и времени падения). Функциональная связь характерна для физико-химических процессов.

В социально-гигиенических исследованиях, а также в клинической медицине и биологии зависимости между явлениями носят характер - характер корреляционной связи. При корреляционной связи значению каждой средней величины одного признака соответствует несколько значений другого взаимосвязанного с ним признака. Всем известно, что рост и масса тела человека связаны между собой. У группы лиц с одинаковым ростом наблюдаются различные колебания массы тела. Однако эти колебания массы тела варьируют в определенных размерах - вокруг своей средней величины.

Между уровнем температуры тела человека и числом сердечных сокращений существует также зависимость. При одинаковой температуре тела у различных людей наблюдаются индивидуальные колебания частоты сердечных сокращений, варьирующие вокруг своей средней.

Важно отметить, что корреляционная связь проявляется лишь в массе наблюдений, т.е. в совокупности.

При установлении корреляционной связи между изучаемыми явлениями перед специалистами каждой области науки стоит задача по изысканию причиной связи, подтверждающей зависимость одного явления от другого, или двух явлений от третьего (от общей их причины). Статистика позволяет исследователю измерить связи, обосновать выводы и наглядно их иллюстрировать.

Используя методы корреляции, важно помнить о возможности измерять связь между различными признаками только лишь в качественно однородной совокупности. Нельзя, например, сопоставлять рост и массу тела людей, состоящих из лиц разного пола и возраста.

Корреляция может быть представлена в виде:

· таблицы

· графика

· коэффициента корреляции

Таблицы и графики дают лишь представление о наличии и направлении связи. Так, между температурой воздуха и числом случаев бронхита существует корреляционная связь. При этом с повышением температуры воздуха число бронхитов уменьшается. Об этой закономерности можно судить по данным, представленным в таблице и на графике. Однако измерить и оценить статистическую достоверность этой связи можно лишь при помощи специального коэффициента корреляции (r_xy) и его средней ошибки (m_r).

Коэффициент корреляции (r_xy) одним числом измеряет силу связи между изучаемыми явлениями и дает представление о ее направлении.

По направлению связь может быть прямой и обратной:

· при прямой связи с увеличением значений одного признака возрастает среднее значение другого признака. Например: с повышением температуры тела увеличивается частота пульса у большинства инфекционных больных; с увеличением роста ребенка увеличивается масса его тела. Коэффициент корреляции, характеризующий прямую связь, обозначается знаком плюс (+).

· при обратной связи: с увеличением одного признака убывает среднее значение другого признака. Например, чем ниже температура воздуха в осенний период, тем выше заболеваемость детей острым бронхитом. Коэффициент корреляции, характеризующий обратную связь, обозначается знаком минус (-). (Табл. 1).

По силе связи коэффициенты корреляции колеблются от единицы (полная связь) до нуля (отсутствующие связи). Чем больше среднему значению одного признака соответствует значений другого признака, тем выше сила связи между ними.

Таблица 1

Схема оценки силы и направления корреляционной связи

по коэффициенту корреляции

 

Сила связи	Прямая (+)	Обратная (-)
Полная	+ 1,0	- 1,0
Сильная	От + 1,0 до + 0,7	От - 1,0 до - 0,7
Средняя	От + 0,3 до + 0,7	От - 0,7 до - 0,3
Слабая	от 0 до + 0,3	от - 0,3 до 0
Отсутствует связь

 

При небольшом числе наблюдений (n £ 30), при не сгруппированных данных коэффициент корреляции определяется по следующей формуле:

, где

х и у - преемственные варианты сопоставляемых вариационных рядов,

d_х и d _у - отклонение каждой переменной (варианты) от своей средней арифметической (М_х и М_у).

 

Ошибка коэффициента корреляции. Для того чтобы убедиться в том, что коэффициент корреляции, вычислительный по данным выборочного исследования, будет соответствовать размеру связи в генеральной совокупности, необходимо определить среднюю ошибку коэффициента корреляции (m_r) и критерий t:

;

;

t оценивается по таблице критерия t, где при n = n-2 (n - число парных вариантов) будет соответствовать вероятности наличия связи (p).

Кроме того, для оценки достоверности коэффициента корреляции можно использовать специальную таблицу для малых выборок (приложение 1). Преимущество этой таблицы заключается в том, что полученную величину коэффициента корреляции можно оценить без предварительных расчетов m_r и t, а путем сравнения r_ху со стандартным коэффициентом корреляции, рассчитанным и представленным в приложении 1 для различной степени вероятности и различного числа наблюдений. Методика пользования таблицей: в вертикальном первом ряду представлены значения n = (n - 2), в верхней строке - желательная степень вероятности наличия связи (p), при которой коэффициент корреляции можно считать достоверным. Цифры внутри таблицы - стандартные коэффициенты корреляции. Вычисленный r_ху должен быть ³ r_{табл. (стандарт)}.

В некоторых случаях измерение направления и силы связи можно осуществлять с помощью так называемого коэффициента ранговой корреляции (r) и его ошибки (m_r).

Коэффициент ранговой корреляции для измерения взаимосвязи между парными признаками применяют при следующих условиях:

1) при небольшом числе наблюдений (не более 30 парных величин);

2) когда нет необходимости в точных расчетах уровня силы связи, а нужны лишь ориентировочные данные;

3) когда признаки имеют не только количественные, но и качественные (описательного характера) значения;

4) когда ряды распределения имеют открытые варианты (например, < 20 или > 40).

При расчете коэффициента ранговой корреляции (r) не имеет значения характер связи: прямолинейная или криволинейная.

Формула расчета:

,

где r - коэффициент ранговой корреляции,

d - разность рангов,

n - число пар.

Формула расчета ошибки коэффициента ранговой корреляции:

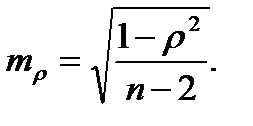
Оценка достоверности r осуществляется по тем же принципам, как и r_ху с помощью критерия t и числа степени свободы n;

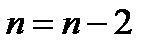
Результаты сравниваются с табличными критериями t_табл.

Задача-эталон 1

Коэффициент корреляции Спирмена (ρ или r_s)

Требуется определить размер связи между уровнем концентрации фтора в питьевой воде и числом лиц, пораженных флюорозом (в процентах к числу обследованных) (табл. 2).

Таблица 2

Распространенность флюороза среди населения, употребляющего воду

с различным содержанием фтора

Содержание фтора в воде, мг/л	Процент пораженных флюорозом	Порядковый номер (ранг)	Разность рангов	Квадрат разности рангов
х	у	х1	у1	d (х1-у1)	d2
Низкое 0,5	0,0				0,0
Оптимальное 1,0	3,0				0,0
Условно-допустимое 1,5	15,0				0,0
Повышенное 3,5	98,0		4,5	-0,5	0,25
Недопустимое 5,0	98,0		4,5	+0,5	0,25
					Sd2=0,5

 

(связь сильная и прямая);

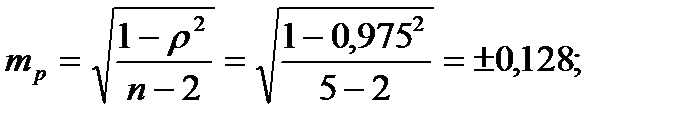
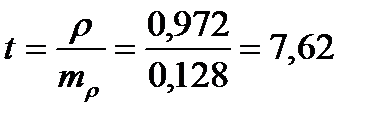, что соответствует вероятности достоверности более 99%

Вывод: между уровнем концентрации фтора в питьевой воде и числом лиц, пораженных флюорозом, наблюдается прямая и сильная связь, так как коэффициент ранговой корреляции составил ρ= +0,975, уровень значимости р<0,01. Таким образом, с увеличением содержания фтора в воде увеличивается распространенность флюороза среди населения.

Задача-эталон 2

Коэффициент корреляции Пирсона (r_xy)

Требуется определить, имеется ли зависимость между температурой тела и частотой пульса (условные данные) (табл. 3).

Последовательность расчета:

1. Построить вариационные ряды из парных признаков х и у.

2. Определить их средние величины - М_x и М_g.

3. Найти d - отклонение каждой варианты от средней для ряда x (d_x = x - M_x) и для ряда y(d_y = y - M_у).

4. Полученные отклонения перемножить (d_x*d_y) и просуммировать (åd_x*d_y).

5. Каждое отклонение возвести в квадрат и суммировать по ряду х - å d_x² и по ряду у - å d_у².

6. Определить произведение å d_x² · å d_у² и из произведения

7. Рассчитать r_xy по формуле: .

 

 

Таблица 3

Зависимость между температурой тела и частотой сердечных сокращений

Температура тела, х	Частота пульса в минуту, у	dх	dу	dx*dy	dх2	dу2
		-2	-20
		-2	-10
		+2	+10
		+2	+20
åх=190 Мх=38	åу=400 Му=80	ådx=0	ådу=0	å dx·dу =120	å dx2=16	å dу2=1000

 

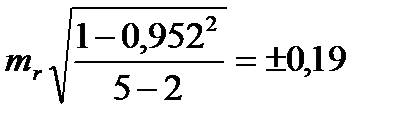
что соответствует вероятности достоверности более 99%

Вывод: между температурой тела и частотой сердечных сокращений выявлена сильная прямая корреляционная связь, так как коэффициент корреляции составил r= +0,952, уровень значимости р<0,01. Таким образом, с увеличением температуры тела увеличивается частота сердечных сокращений.

Приложение1

Стандартные коэффициенты корреляции, которые считаются достоверными

(по Л.С. Каминскому)

 

Число степеней свободы n=n-2	Уровень вероятности p (в %)	Число степеней свободы n=n-2	Уровень вероятности p (в %)
95,0	98,0	99,0	95,0	98,0	99,0
	0,997	0,999	0,999		0,532	0,612	0,661
	0,950	0,980	0,990		0,514	0,592	0,641
	0,878	0,934	0,959		0,497	0,574	0,623
	0,811	0,882	0,917		0,482	0,558	0,606
	0,754	0,883	0,874		0,468	0,542	0,590
	0,707	0,789	0,834		0,456	0,528	0,575
	0,666	0,750	0,798		0,444	0,516	0,561
	0,632	0,716	0,765		0,433	0,503	0,549
	0,602	0,685	0,735		0,423	0,492	0,537
	0,576	0,658	0,708		0,381	0,445	0,487
	0,553	0,634	0,684		0,349	0,409	0,449

 

Подпись автора методической разработки_____________

«29.06.2016г.»

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: