Колебательные процессы. Виды колебаний. Свободные гармонические колебания и их характеристики.

Колебания – процессы в той или иной мере повторяющиеся с течением времени. Свободные, вынужденные, авто колебания. От фаз: механ., эл. магн., эл. механ. Механические колебания – движения тел, которые повторяются точно или приблизительно с течением времени. Если повторение происходит через строго равные промежутки времени, то колебания называются периодическими.

Колебательная система – система тел, которая может совершать колебательные движения. У колебательной системы есть положение равновесия – положения тел, при которых они могут находиться в покое (не совершать колебаний).

Свободные колебания – колебания, возникающие в результате внутренних сил, т. е. действующих между телами колебательной системы.

Дифференциальное уравнение гармонических колебаний пружинного маятника и его решение. Характеристики колебаний пружинного маятника.

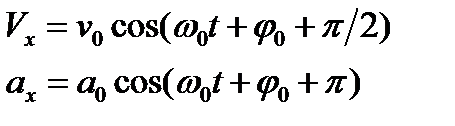Пружинный маятник – груз, соединенный с абсолютно упругой пружиной и совершающий колебания под действием силы упругости

Уравнение гармонических колебаний пружинного маятника. Период колебаний пру­жинного маятника.

, решение уравнение

Период происходит с собственной циклической частотой F_упр = - кх

Дифференциальное уравнение гармонических колебаний физического маятника и его решение. Характеристики колебаний физического маятника.

Физ. маятник – твердое тело, которое вращается относительно оси, не проходящей через центр тяжести. Вращение происходит под действием силы тяжести.

Частота

 

Период

 

 

53. Математический маятник. Приведенная длина физического маятника.

Материальная точка, подвешенная на невесомой нерастяжимой нити

 

Приведенная длина физического маятника – длина математического маятника, частота колебаний которого равна частоте колебаний рассматриваемого физического маятника.

 

Скорость и ускорение материальной точки, совершающей гармонические колебания

Энергия материальной точки, совершающей гармонические колебания.

Гар-кие колебания в колебательном контуре. Превращения энергии в контуре.

Гармонические колебания – колебания, для которых смещение зависит от времени по закону синуса или косинуса.

Сложение гармонических колебаний одинаковой частоты и одинакового направления. Биения.

Биения – колебания, для которых амплитуда является медленной периодической функцией времени.

Метод векторных диаграмм – взаимно-однозначное соответствие между колебательным процессом и вектором, вращающимся с постоянной угловой скоростью: амплитуда равна длине вектора; циклическая частота – угловой скорости; начальная фаза – начальному углу с горизонтальной осью; фаза – текущему углу с горизонтальной осью; смещение – проекции вектора на горизонтальную ось.

Уравнение биений. Период биений.

Начальная фаза и амплитуда.

 

 

58. Сложение перпенд-х гарм-х колебаний одинаковой частоты. Фигу ры Лиссажу.

Уравнение траектории результирующего движения при сложении перпендикулярно направленных колебаний одной частоты

 

 

уравнение эллипса

 

Такие колебания эллиптически поляризованные т.к. описывает эллипс за время

 

Ориентация осей эллипса и их размеры зависят от амплитуд и разности фаз.

При А₁ = А₂ – круг (колебания поляризованные по кругу). А =(А²₁+А²₂)^1/2 –линейно поляризованные колебания. В общем случае траектории зависят от соотношения частот, амплитуд и разности фаз. Это фигуры Лиссажу.

 

Фигура Лиссажу при двукратном отношении частот

 

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: