 |
Расчет переходных процессов при коммутации ключа К1
|
|
|
|
ВВЕДЕНИЕ
Представлен расчет переходных процессов в цепи двумя методами:
1) классическим методом
2) операторным методом
Построены графики зависимостей напряжений и токов на конденсаторе и катушке индуктивности от времени.
КЛАССИЧЕСКИЙ МЕТОД
Разобьем поставленную задачу на две части: расчет переходных процессов в цепи после замыкания ключа К1, и расчет переходных процессов при замыкании ключа К2, применяя полученные условия после коммутации ключа К1.
Расчет переходных процессов при коммутации ключа К1
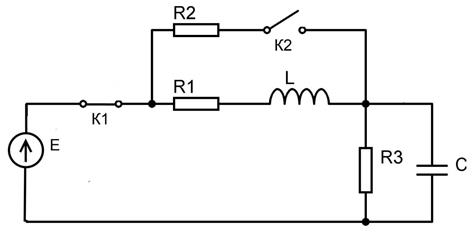
Начертим исходную цепь с учетом того, что ключ К2 разомкнут (рисунок 2)
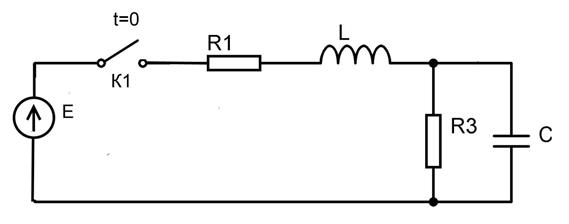
 Независимые начальные уравнения.
Независимые начальные уравнения.
uc(0-) = uc(0) = uc(0+);
i c(0-) = i c(0) = i c(0+).
До коммутации.
uc(0-) = 0 и i c(0-) = 0, следовательно, uc(0) = uc(0+) = 0 и i (0) = i (0+) = 0. Изобразим цепь после коммутации К1 (рисунок 3)
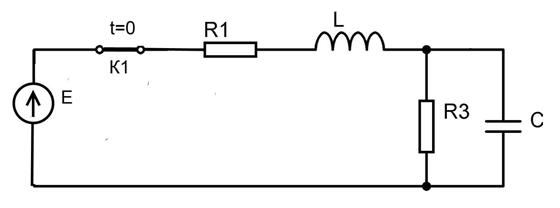

Изобразим схему цепи для подсчёта входного сопротивления (рисунок 4)
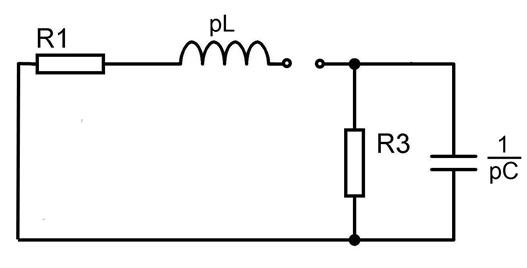
Рисунок 4 – Схема для подсчета входного сопротивления
Составим характеристическое уравнение для изображенной на рисунке 4 схемы методом входного сопротивления [1]. Сделаем формальную замену jω на р и приравняем z к нулю:
Z(p)=0
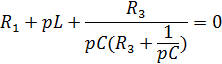
Подставив в полученное уравнение параметры цепи, решим уравнение с помощью MathCAD.

Рисунок 5 – Решение уравнения в MathCAD
Получили 2 комплексных сопряженных корня:

Отсюда α=-35000, ω= 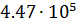
Поскольку корни характеристического уравнения комплексно – сопряжённые, то свободная составляющая тока имеет вид:
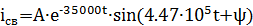
Процесс носит колебательный характер.
Т.к. 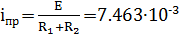 A
A
То полный ток:
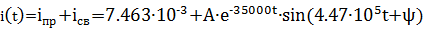 , А.
, А.
Определим постоянные интегрирования А и ψ.
Первое уравнение для расчёта А и φ получаем из условия i (0) = 0, т.е.
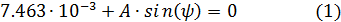
Для получения второго уравнения запишем для цепи уравнение по второму закону Кирхгофа:
|
|
|
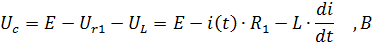
Где
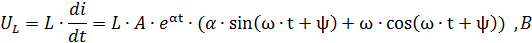
Получим второе уравнение для расчёта А и ψ из условия Uc(0) = 0
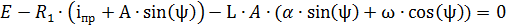
Так как i(0)=0 то на 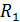 не будет падения напряжения тогда уравнение примет вид:
не будет падения напряжения тогда уравнение примет вид:
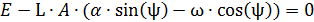
Получим второе уравнение для расчёта постоянных интегрирования.
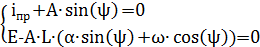
Решив систему уравнений, получаем
ψ= 173.6о или φ= 3.03рад.
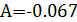
Тогда:
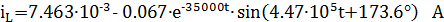
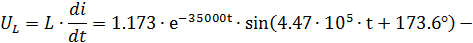
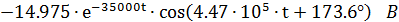
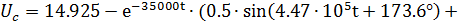
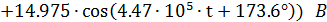
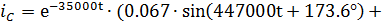
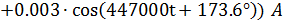
Расчет переходных процессов при коммутации ключа К2

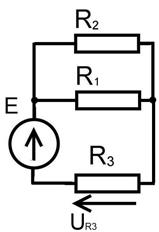 |
Рисунок 7 – Схема цепи в принужденном режиме
Из рисунка 7 видно, что
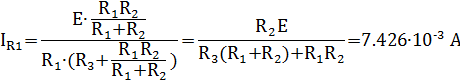
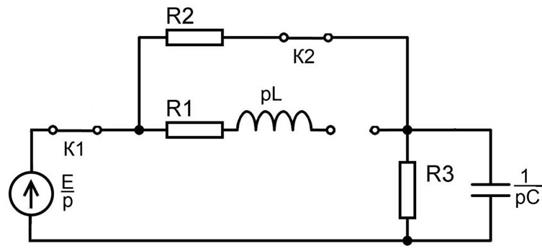
Рисунок 8 – Схема для подсчета входного сопротивления
Составим характеристическое уравнение для изображенной на рисунке 8 схемы методом входного сопротивления [1]. Сделаем формальную замену jω на р и приравняем z к нулю:
z(p)=0
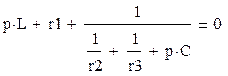
Подставив в полученное уравнение параметры цепи, решим уравнение с помощью MathCAD.
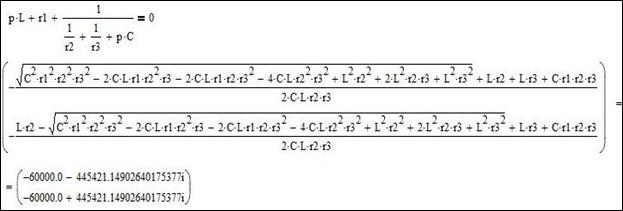
Рисунок 9 – Нахождение корней уравнения в MathCAD
Получили пару сопряженных комплексных корня:
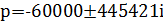
Поскольку корни характеристического уравнения комплексно – сопряжённые, то свободная составляющая тока на индуктивности имеет вид:
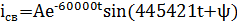
Полный ток на индуктивности:
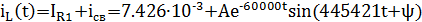
Значения тока на катушке и напряжения на конденсаторе для времени τ, согласно уравнениям, полученным после коммутации первого ключа равны:
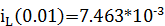 A
A
 В
В
Определим постоянные интегрирования А и ψ.
Начальные условия:
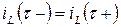 и
и 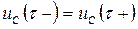
Первое уравнение для расчёта А и ψ:
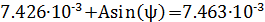
Для получения второго уравнения запишем для цепи уравнение по закону Кирхгофа для момента t = 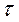 +:
+:
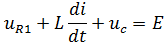
Учтём независимые начальные условия и получим:
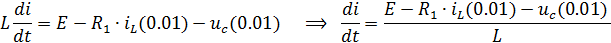
Теперь продифференцируем выражение полного тока:
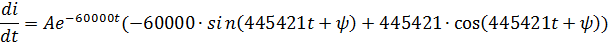
Второе уравнение для расчёта постоянных интегрирования:
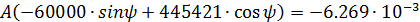
Решим систему из полученных уравнений:
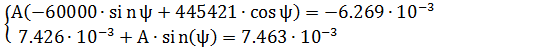
Решив систему уравнений, получаем
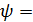 97.627о или
97.627о или 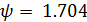 рад.
рад.
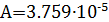
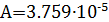
Тогда:
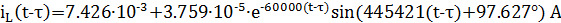
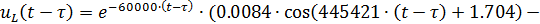
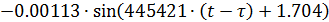 В
В
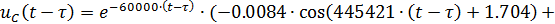

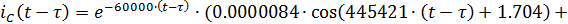
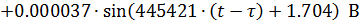
2.ОПЕРАТОРНЫЙ МЕТОД
Расчет переходных процессов при коммутации ключа К1
Составим операторную схему замещения после замыкания ключа К1[1]:
|
|
|
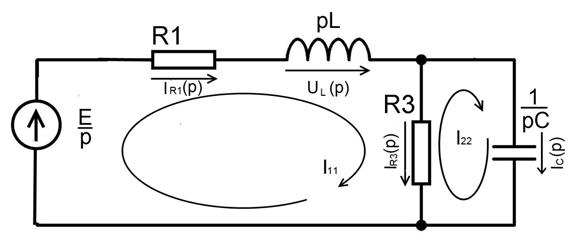
Рисунок 10– Операторная схема замещения
На схеме не изображены дополнительные источники энергии, соответствующие изображениям емкости и индуктивности, так как в начальный момент времени токов и напряжений в цепи не было, а, следовательно, их номинальные значения нулевые, в схеме остаются только их внутреннее сопротивление, а сопротивление идеального источника ЭДС равно нулю.
Составим систему уравнений для контурных токов в операторной форме:
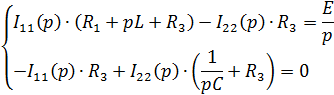
Решим полученную систему уравнений с помощью MathCAD:

Рисунок 16 – Решение системы уравнений и нахождение оригиналов изображений в MathCAD
Получаем:
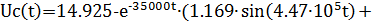
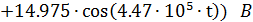
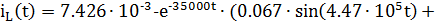
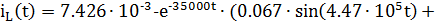
|
|
|


