 |
Логика работы программы SUNPL.EXE
|
|
|
|
Назначение программы
Программа SUNPL.EXE предназначена для расчета траекторий межпланетных перелетов от одной планеты Солнечной системы к другой с использованием двигателей большой тяги (импульсных перелетов), а также для расчета единичного пертурбационного (гравитационного) маневра. Программа используется при выполнении курсового и дипломного проектирования студентами, проходящими обучение по специальностям 1306 «Ракетостроение» и 1307 «Космические летательные аппараты и разгонные блоки».
Основные характеристики межпланетных перелетов
Из всего многообразия межпланетных перелетов практический интерес представляют перелеты от Земли к другим планетам Солнечной системы. Обратные перелеты от планет к Земле в настоящее время рассматриваются только для Марса (доставка грунта, в перспективе – пилотируемая экспедиция).
Траектории перелета к планетам — траектории, по которым возможен полёт КА от Земли до сближения с планетой Солнечной системы (планетой назначения) на расстояние меньше сферы действия планеты.
Основная схема полёта. Непосредственно из точки старта РН выводит КА на промежуточную (опорную) орбиту ИСЗ. Включение в схему полёта промежуточной орбиты позволяет энергетически экономно реализовать выведение КА из любой заданной точки старта на поверхности Земли на траекторию перелёта (или для планеты назначения осуществить посадку в любую точку на её поверхности, повышения точности посадки на планету по сравнения с посадкой с пролетной траектории – «попаданием в планету»). Траекторные измерения во время движения КА по промежуточной орбите позволяют уточнить параметры его движения для проведения необходимой коррекции.
|
|
|
Промежуточная орбита ИСЗ используется во всех схемах выведения КА на траектории полёта к планетам (напр., КА «Марс», «Венера») и к Луне (начиная с КА «Луна-4»). Т. к. выведение на промежуточную орбиту ИСЗ происходит с вращающейся Земли, то выбором времени старта можно без каких-либо дополнительных энергетических затрат реализовать любое значение долготы восходящего узла орбиты на экваторе Земли. Выбором времени старта с промежуточной орбиты ИСЗ (путём разгона КА в плоскости орбиты) также без дополнительных затрат достигается необходимая ориентация траектории перелёта в плоскости этой орбиты. Для полярной промежуточной орбиты ИСЗ таким путём, напр., можно получить любое направление вектора скорости КА относительно Земли на выходе из её сферы действия. Для других наклонений промежуточных орбит ИСЗ существует конус направлений векторов скорости, который не может быть реализован такой схемой. Переход КА с промежуточной орбиты ИСЗ на траекторию перелета к планете назначения осуществляется дополнительным разгоном КА (с помощью разгонного блока и/или собственной ДУ КА). Необходимые кинематические параметры в начале пассивного участка траектории перелета получаются выбором момента времени старта с Земли, момента времени старта с промежуточной орбиты ИСЗ и значения импульса, сообщаемого КА при старте с промежуточной орбиты ИСЗ.
Траектория перелета содержит три последовательных участка:
1. геоцентрический гиперболический участок траектории полёта внутри сферы действия Земли, на котором продолжающееся несколько суток движение КА определяется полученной после разгона с промежуточной орбиты ИСЗ начальной скоростью движения и влиянием главным образом гравитационного притяжения Земли;
2. основной по продолжительности полёта гелиоцентрический (как правило, эллиптический) участок полёта вне сфер действия Земли и планеты назначения, на котором движение КА так же, как и движение планет, происходит в основном под действием гравитационного притяжения Солнца;
|
|
|
3. планетоцентрический гиперболический участок траектории, расположенный внутри сферы действия планеты назначения, на котором определяющая сила — гравитационное притяжение планеты.
По условиям сближения КА с планетой назначения различают полёты:
· по пролётным траекториям (напр., «Венера-1, -2», «Марс-1») или облётным траекториям, используемым для проведения физ. измерений в окрестности планеты назначения и в межпланетном пространстве в процессе полёта (в некоторых вариантах перелетов пролёт около какой-либо планеты проводится с целью использования её гравитационного поля для формирования последующего участка траектории, (т.е. совершения гравитационного маневра);
· по траекториям, пересекающим поверхность планеты, применяемым для проведения физ. измерений в процессе движения КА в атмосфере планеты или (и) мягкой посадки КА на поверхность планеты (напр. «Венера-4» — «Венера-14»), т.е. траекториям «попадания»;
· по траекториям, выводящим КА на орбиту искусств, спутника (ИС) планеты (напр., «Маринер-9», «Марс-5»; в некоторых схемах полёта движение КА по орбите ИС планеты является промежуточным этапом для последующей посадки КА на поверхность планеты с использованием РД или (и) атмосферы планеты для торможения КА);
· по траекториям, реализующим комбинированные варианты; так, напр., при сближении с планетой от КА отделяется спускаемый аппарат, реактивный импульс переводит её на траекторию сближения с поверхностью планеты с целью проведения физ. измерений в атмосфере планеты или (и) мягкой посадки на её поверхность (в это же время КА продолжает движение по пролётной траектории или переходит на орбиту ИС планеты, напр. «Марс-2», «Марс-6»).
Для достижения необходимой точности выполнения условий сближения КА с планетой назначения в процессе полёта (после уточнения параметров движения по траекторным измерениям) проводятся коррекции движения, которые существенно изменяют параметры планетоцентрического участка траектории и практически не изменяют основных характеристик траектории перелета на её геоцентрическом и гелиоцентрическом участках.
|
|
|
Энергетическая проблема и гомановские перелёты. Если отвлечься от ограниченности допустимых энергетических затрат, то теоретически оказываются возможными траектории перелета с произвольно заданными датами старта tс и датой прилёта tп к планете назначения. Однако при этом для некоторых значений tс и tп потребная для осуществления такого полёта характеристическая скорость будет чрезмерно большой. Более того, и для большинства комбинаций tс и tп потребные энергетические затраты на реализацию соответствующей траектории превосходят существующие возможности (для заданных РН и РБ с ростом значения энергетических затрат снижается масса полезного груза, который может быть выведен на данную траекторию полёта). Для практического применения оказываются пригодными лишь т. н. энергетически оптимальные траектории и близкие к ним соответствующие определенным диапазонам изменения параметров tс и tп.
Основные характеристики оптимальных траекторий перелета можно уяснить из рассмотрения упрощённой модели Солнечной системы, в которой предполагается, что все планеты движутся по круговым орбитам, расположенным в одной плоскости. Для перелёта с одной круговой орбиты на другую энергетически оптимальным является перелёт по эллипсу Гомона (рис. 1).
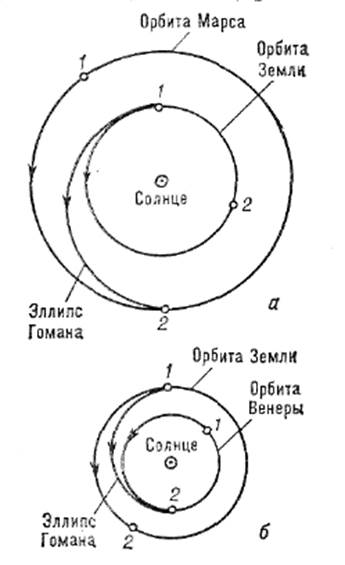
Рис. 1 - Схема траекторий полётов: а — к Марсу (внешняя планета); б — к Венере (внутренняя планета); 1 - положение планет в момент старта с Земли; 2 – положение планет в момент сближения КА с планетой
При этом различают полёт к внешним планетам Солнечной системы, т. е. к планетам, орбита которых расположена дальше от Солнца, чем орбита Земли, напр. Марс, Юпитер (рис. 1, а), и полёты к внутренним планетам, т. е. к планетам, орбита которых расположена ближе к Солнцу, чем орбита Земли,— Венера, Меркурий (рис. 1, б). Эллипс Гомана касается орбиты Земли и орбиты планеты назначения таким образом, что при полёте к внешней планете на орбите Земли расположен его перигелий, а на орбите планеты назначения — афелий, а при полёте к внутренней планете на орбите Земли находится его афелий. В начале движения КА по эллипсу Гомана при достаточном удалении от Земли (примерно на границе её сферы действия) его гелиоцентрическая скорость почти параллельная орбитальной скорости движения Земли и больше её (для полёта к внешним планетам) или меньше (для полёта к внутренним планетам) на ΔV1. Т. о., для выведения КА на гомановскую траекторию перелёта (в результате разгона КА у Земли) он должен иметь при выходе из сферы действия Земли геоцентрическую скорость, близкую по значению к ΔV1. В зависимости от задачи (внешняя или внутренняя планета) эта скорость должна быть ориентирована примерно по направлению орбит, скорости движения Земли или против неё. Аналогично при сближении с планетой назначения в её сфере действия скорость движения КА будет близка по направлению к орбитальной скорости планеты, а по значению меньше (для внешней планеты) или больше её (для внутренней планеты) на ΔV2. Одной из основных характеристик траектории перелета является угловая дальность — угол между радиус-векторами, проведёнными из центра Солнца к планете старта в момент времени tс и к планете назначения в момент tп. От этой величины существенно зависят энергетические затраты. Для гомановского перелёта этот угол равен 180° и время перелёта Δtп от орбиты планеты старта до орбиты планеты назначения определяется однозначно. Поэтому для приближенного описания траектории перелета гомановским перелётом необходимо, чтобы угол между радиус-вектором планеты старта r1 (tс) в момент tс и радиус-вектором планеты назначения г2 (tп) в момент времени tп = tс + Δtп составлял 180°. Это условие накладывает определенные требования на взаимное расположение планет в момент старта. Так как планеты движутся вокруг Солнца с почти постоянными и неравными угловыми скоростями, это условие выполняется примерно периодически с периодом Тс, равным периоду обращения планеты относительно Земли, или синодическому периоду обращения планеты. Некоторые характеристики гомановских перелётов Земля — небесное тело приведены в табл. 1.
|
|
|
Энергетически оптимальный обратный перелёт от планеты к Земле в гомановском приближении для круговых планетных орбит, лежащих в одной плоскости, принципиально ничем не отличается от прямого полёта от Земли. Поэтому можно воспользоваться гомановским приближением для оценки характеристик перелёта Земля — планета — Земля. Следует только отметить, что энергетически оптимальное взаиморасположение планеты и Земли для обратного перелёта реализуется не сразу по достижении планеты в прямом полёте. Вследствие этого в рассматриваемой задаче появляется важная характеристика — время ожидания Δtож КА у планеты, отсчитываемое от момента времени прилёта к планете до момента времени обратного старта. Значение Δtож и суммарное время ΔtΣ экспедиции Земля — планета — Земля также приведены в табл. 1.
|
|
|
Таблица 1 – Характеристики гомановских перелетов Земля – планета
| Характеристики | Планета | |||||||
| Меркурий | Венера | Марс | Юпитер | Сатурн | Уран | Нептун | Плутон | |
| Время полета Δtп, годы | 0,29 | 0,40 | 0,71 | 2,74 | 5,05 | 16,04 | 30,62 | 45,80 |
| Синодический период Тс, годы | 0,34 | 1,60 | 2,13 | 1,09 | 1,03 | 1,01 | 1,01 | 1,00 |
| Скорость на сфере действия Земли ΔV1, км/с | 7,50 | 2,53 | 2,98 | 8,70 | 10,30 | 11,30 | 11,70 | 11,85 |
| Скорость на сфере действия планеты назначения ΔV2, км/с | 9,56 | 2,80 | 2,65 | 5,65 | 5,49 | 4,56 | 3,94 | - |
| Время ожидания Δtож, годы | 0,16 | 1,28 | 1,24 | 0,58 | 0,93 | - | - | - |
| Суммарное время полета Земля – планета – Земля, годы | 0,76 | 2,08 | 2,66 | 6,05 | 13,03 | - | - | - |
Влияние эллиптичности планетных орбит и их взаимного наклонения. В реальной Солнечной системе орбиты планет не являются круговыми, и плоскость орбиты планеты назначения наклонена к плоскости орбиты планеты старта. Однако так как эксцентриситеты орбит и их взаимные наклонения малы, то траектории оптимальных перелётов оказываются качественно близки к гомановским перелётам, хотя количеств, поправки к энергетическим оценкам, которые возникают при точном решении задачи перелёта, могут быть существенны. Для реальных планетных орбит локально оптимальными по-прежнему оказываются перелёты, когда угловая дальность между радиус-векторами планеты старта r1(tс) в момент tс и радиус-вектором планеты назначения г2(tп) в момент времени tп = tс + Δtп оказывается близкой к 180°. Такая конфигурация также повторяется через синодический период. Однако если рассмотреть последовательность локально оптимальных положений планет, отделённых друг от друга по времени целым числом синодических периодов, то им будет соответствовать различное положение векторов r1(tс) и г2(tп) на их орбитах, хотя угловая дальность между ними будет близка к 180°. При этом из-за эллиптичности орбит и их взаимного наклонения в различные периоды будут различными: значения этих векторов, соответствующие им векторы орбитальных скоростей движения планет и составляющая Z2 вектора г2(tп), ортогональная плоскости орбиты планеты старта. Это приводит к тому, что локально оптимальные траектории, отделённые по времени старта одним или несколькими синодическими периодами, различаются по основным энергетическим характеристикам. Различие носит также примерно периодический характер (с периодом Твп, равным периоду великих противостояний планеты старта и планеты назначения). Через период Твп векторы r1(tс) и г2(tп), соответствующие локально оптимальным решениям, оказываются расположенными приблизительно в тех же местах своих орбит. Значение периодов великих противостояний относительно Земли для Меркурия — 1 год, Венеры — 8 лет, Марса — 15,8 года.
Для получения общих оценок энергетических затрат, напр. для полёта Земля -Марс, можно на время отвлечься от конкретных дат старта и прилёта и рассмотреть задачу оптимального перелёта с орбиты Земли к Марсу, задавая различные его положения d на орбите и считая при этом, что Земля занимает оптимальное положение. Значение ΔV1, полученное при решении такой задачи, приведено на рис. 2, а. На рис. 2, б приведены соответствующие данному d значение радиус-вектора Марса и его координата Z2. Для сравнения на рисунках отмечены значения параметров, отвечающих круговым плоским орбитам. Из рис. 2, а видно, что для различных периодов значение ΔV1 в локально оптимальных решениях может отличаться на 1,5 км/с (в плоской круговой модели орбит планет ΔV1~3 км/с). Для реализации пролётной или облётной траектории полёта величина ΔV1 косвенно характеризует потребные энергетические затраты. Представляет интерес характеристическая скорость W1, которую необходимо иметь при разгоне с промежуточной орбиты ИС планеты старта для получения потребного значения ΔV1. Значения даты старта tс, продолжительности полёта Δtп, скорости W1 и ΔV2, вычисленные с учётом эллиптичности планетных орбит и их взаимных наклонений, приведены в таблицах 2—4: для локально оптимальных перелётов Земля — Марс (табл. 2), Земля — Венера (табл. 3) и Земля — Юпитер (табл. 4) (при этом промежуточная орбита ИСЗ предполагается круговой, высотой 200 км. В табл. 2—4 приведены параметры оптимальных траекторий перелета вплоть до 1991 года.
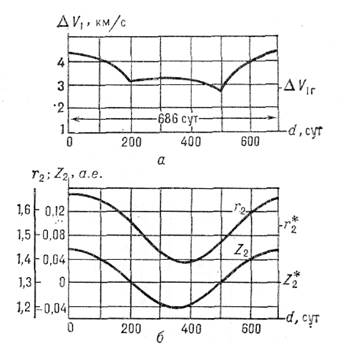
Рис. 2 - Графические зависимости скорости ΔV1 (а), необходимой для полёта к Марсу, и гелиоцентрического радиус-вектора г2 Марса и его составляющей Z2 (б), ортогональной плоскости эклиптики, от положения Марса на орбите, определяемого параметром d; ΔV1r отмечает значение ΔV1 в гомановском приближении; г2*, Z2* — значения г2 и Z2 для плоской модели круговых планетных орбит

Рис. 3. Линии равных значений скорости ΔV1 для полёта Земля — Марс в плоскости с координатами tc и Δtп (tc — дата старта, Δtп — время полёта). Цифрами около линий указана величина ΔV1 в км/с; минимум скорости ΔV1= 2,97 км/с достигнут при tc = 10.3.1969 и Δtп =180 сут.
Таблица 2 – Характеристики траекторий полета к Марсу
| Дата старта tc | Время полета Δtп, сут. | Характеристическая скорость W1, км/с | Скорость на сфере действия Марса ΔV2, км/с |
| 25.5.1971 | 3,43 | 2,84 | |
| 30.7.1973 | 3,72 | 3,00 | |
| 15.9.1975 | 3,91 | 3,75 | |
| 19.10.1977 | 3,83 | 4,04 | |
| 3.11.1979 | 3,48 | 2,87 | |
| 18.12.1981 | 3,48 | 5,19 | |
| 8.2.1984 | 3,47 | 5,49 | |
| 22.4.1986 | 3,43 | 3,35 | |
| 5.7.1988 | 3,59 | 2,77 | |
| 30.8.1990 | 3,77 | 3,46 |
Таблица 3 – Характеристики траекторий полета к Венере
| Дата старта tc | Время полета Δtп, сут. | Характеристическая скорость W1, км/с | Скорость на сфере действия Марса ΔV2, км/с |
| 18.8.1970 | 3,60 | 5,40 | |
| 28.3.1972 | 3,77 | 6,06 | |
| 10.11.1973 | 3,82 | 4,80 | |
| 10.6.1975 | 3,51 | 3,61 | |
| 10.1.1977 | 3,56 | 4,39 | |
| 16.8.1978 | 3,60 | 5,33 | |
| 26.3.1980 | 3,76 | 6,05 | |
| 8.11.1981 | 3,82 | 4,92 | |
| 10.6.1983 | 3,52 | 3,53 | |
| 7.1.1985 | 3,56 | 4,29 | |
| 13.8.1986 | 3,59 | 5,26 | |
| 24.3.1988 | 3,76 | 6,05 | |
| 15.11.1989 | 3,82 | 5,04 | |
| 10.6.1991 | 3,54 | 3,54 |
Таблица 4 – Характеристики траекторий полета к Юпитеру
| Дата старта tc | Время полета Δtп, сут. | Характеристическая скорость W1, км/с | Скорость на сфере действия Марса ΔV2, км/с |
| 3.1.1970 | 6,24 | 5,69 | |
| 30. 1.1971 | 6,30 | 6,47 | |
| 4. 3.1972 | 6,42 | 7,05 | |
| 9. 4.1973 | 6,53 | 7,12 | |
| 18. 5.1974 | 6,56 | 6,66 | |
| 30. 6.1975 | 6,45 | 5, 71 | |
| 29. 7.1976 | 6,47 | 5,97 | |
| 3. 9.1977 | 6,65 | 6,48 | |
| 6.10.1978 | 6,78 | 6,86 | |
| 7.11.1979 | 6,77 | 6,79 | |
| 7.12.1980 | 6,60 | 6,21 | |
| 4. 1.1982 | 6,23 | 5,69 | |
| 3. 2.1983 | 6,32 | 6,59 | |
| 3. 4.1984 | 6,44 | 7,08 | |
| 15. 4.1985 | 6,54 | 7,09 | |
| 23. 5.1986 | 6,56 | 6,58 | |
| 5. 7.1987 | 6,37 | 5,73 | |
| 30. 8.1988 | 6,49 | 6,03 | |
| 7. 9.1989 | 6,68 | 6,55 | |
| 11.10.1990 | 6,78 | 6,84 |
В силу того, что при небольшом отступлении от локального минимума энергетические затраты растут не очень быстро, для практического использования допустимы не только строго оптимальные даты tс и tп, но и некоторая их окрестность. В этом смысле говорят о цикле оптимальных перелётов как о множестве допустимых перелётов, близких к локально оптимальным (при этом допустимый временной промежуток старта с Земли называют стартовым окном). Для иллюстрации на рис. 3 изображены линии (изолинии) равных значений скорости ΔV1, необходимой для полёта Земля — Марс, в окрестности оптимальной даты старта tc = 10.3.1969 и Δtп = 180 сут. Аналогична картина и при расчёте величины ΔV1 для полёта к другим планетам. Такие поля изолиний позволяют просто решать ряд задач, имеющих важное прикладное значение, как, напр., определение допустимого диапазона дат старта, для которого значение ΔV1 не превосходит заданного, и определение траектории с минимальными энергетическими затратами при заданном времени полёта Δtп. Можно в этой же плоскости tc и Δtп (или tc и tп = tc + Δtп) построить линии равных значений любого другого параметра траектории, представляющего специфический интерес. Таким путём можно провести анализ и выбор траектории полёта не только по энергетическим критериям.
Выше были описаны некоторые характеристики оптимальных траекторий с угловой дальностью полёта, близкой к 180°. Следует заметить, что существуют ещё локально энергетически оптимальные траектории с угловой дальностью полёта, существенно большей 180º. Эти траектории по энергетическим затратам сравнимы с описанными выше. Однако из-за существенно большего времени полёта Δtп эти траектории не использовались на практике.
Энергетические оценки для перелёта на орбиту ИС планеты назначения. Для оценки энергетических возможности реализации облётной или пролётной траектории около планеты назначения достаточно определить только значение характеристической скорости W1, которую необходимо затратить при разгоне КА с промежуточной орбиты ИС планеты старта. Если целью полёта является выведение КА на орбиту ИС планеты назначения, то суммарные энергетические затраты определяются значением W = W1 + W2, где W2 — значение характеристической скорости, которую необходимо иметь для перехода с гиперболического планетоцентрического участка траектории перелета на орбиту ИС планеты. Минимизация W определяет свои локально оптимальные даты tс и tп. Значения W1 и W2 зависят не только от tc и tп, но и от параметров промежуточной орбиты ИС планеты старта (назначения). В табл. 5 приведены характеристики для перелёта с круговой промежуточной орбиты ИСЗ (высота ИС над поверхностью Земли Нкр = 200 км) на круговую орбиту спутника Марса (Нкр = 1000 км). В табл. 6 приведены аналогичные зависимости для перелёта с орбиты ИСЗ (Нкр = 200 км) на орбиту И С Венеры (Нкр = 500 км).
Из сравнения таблиц видно, что величины tc, Δtп и W1 = W — W2 в задачах облёта (пролёта) планеты близки по значению к соответствующим оптимальным величинам для задачи перехода на орбиту ИС планеты. Спец. интерес в табл. 5 и 6 представляет величина W2, непосредственно связанная с задачей перехода на орбиту ИС планеты.
Использование гравитационного влияния планет для формирования траекторий полёта. Как видно из табл. 1, значение ΔV1, т. е. в конечном счёте потребные энергетические затраты, для гомановского перелёта от Земли к планете увеличиваются с удалением орбиты планеты назначения от орбиты Земли (в качестве параметра можно рассмотреть большую полуось орбиты планеты). Стремление уменьшить энергетические затраты или время полёта Δtп стимулировало исследование вариантов перелета, в которых для достижения планеты назначения используется предварительный пролёт мимо другой планеты с целью направленного изменения гелиоцентрической скорости движения за счёт гравитационного воздействия планеты на КА. Изменение параметров движения КА с помощью гравитационного маневра происходит без затрат топлива.
Таблица 5 – Характеристики траекторий полета на орбиту ИС Марса
| Дата старта tc | Время полета Δtп, сут. | Характеристическая скорость | |
| W= W1+W2, км/с | W2, км/с | ||
| 23.5.1971 | 5,61 | 2,19 | |
| 8.8.1973 | 5,85 | 2,07 | |
| 28.9.1975 | 6,14 | 2,06 | |
| 1.11.1977 | 6,00 | 2,05 | |
| 15.11.1979 | 5,96 | 2,45 | |
| 7.1.1982 | 6,52 | 2,79 | |
| 28.2.1984 | 6,42 | 2,75 | |
| 28.4.1986 | 5,79 | 2,36 | |
| 12.7.1988 | 5,99 | 2,08 | |
| 11.9.1990 | 6,07 | 2,06 |
Таблица 6 – Характеристики траекторий полета на орбиту ИС Венеры
| Дата старта tc | Время полета Δtп, сут. | Характеристическая скорость | |
| W= W1+W2, км/с | W2, км/с | ||
| 4.9.1970 | 7,69 | 3,97 | |
| 17.4.1972 | 7, 77 | 3,75 | |
| 25. 11.1973 | 7,30 | 3,37 | |
| 9.6.1975 | 6,88 | 3,31 | |
| 11.1.1977 | 7,40 | 3,84 | |
| 1.9.1978 | 7,68 | 3,98 | |
| 14.4.1980 | 7,78 | 3,77 | |
| 23.11.1981 | 7,34 | 3,38 | |
| 9.6.1983 | 6,92 | 3,35 | |
| 10.1.1985 | 7,38 | 3,82 | |
| 29.8.1986 | 7,67 | 3,98 | |
| 12.4.1988 | 7,80 | 3,79 | |
| 21.11.1989 | 7,37 | 3,46 | |
| 10.6.1991 | 6,94 | 3,30 |
Используя гравитационное возмущения Венеры при старте в некоторые циклы оптимальных полётов к Венере, можно осуществить полёт Земля — Венера — Меркурий с энергетическими затратами, близкими по значению к тем, которые необходимы только для полёта к Венере. В то же время из табл. 1 видно, что для непосредственного (близкого к гомановскому) полёта Земля — Меркурий необходимо получить значение ΔV1 примерно в 3 раза больше, чем для полёта к Венере. Используя возмущающее влияние Венеры, можно энергетически экономным путём реализовать представляющие спец. интерес траектории, приближающиеся к Солнцу на расстояние 0,2…0,3 а. е. При этом в некоторых вариантах целесообразно в окрестности Венеры сообщить КА небольшой дополнительный импульс с помощью РД. Сочетание пертурбационного манёвра и работы РД позволяет расширить диапазон энергетически допустимых дат старта.
Особенно эффективны схемы полёта, в которых используется возмущающее воздействие Юпитера. Гравитационный манёвр в сфере действия Юпитера позволяет вывести КА с энергозатратами, близкими к энергозатратам только для полёта к Юпитеру:
· на траектории полёта к Солнцу с общим временем полёта около трёх лет (для непосредственного полёта Земля — Солнце потребное значение ΔV1 примерно в 3 раза превосходит ΔV1 для полёта к Юпитеру);
· на траектории, при движении по которым КА удаляется на большое расстояние от плоскости орбиты Земли.
Эти варианты представляют большой интерес для исследования межпланетного пространства.
Наиболее эффективен проект полёта КА к дальним планетам с последовательным пролётами около Юпитера, Сатурна и других дальних планет (т.н. «Большой тур»).
Для полётов к нескольким планетам циклы оптимальных перелётов повторяются через период Тс, равный общему наименьшему кратному всех взаимных синодических периодов планет, входящих в маршрут полёта. Так, для «Большого тура» этот период составляет 170—180 лет. Ближайшие циклы оптимальных полётов по таким маршрутам приходились на 1976—79 гг.
Существует несколько более простых вариантов полёта к дальним планетам с пролётом мимо Юпитера (ряд вариантов реализован при полёте КА «Вояджер-1, -2», «Пионер-11»). Некоторые характеристики этих траекторий приведены в табл. 7.
Таблица 7 – Характеристики полета к дальним планетам с пролетом мимо Юпитера
| Маршрут полета | Годы оптимальных циклов | Скорость на сфере действия Земли, км/с | Время полета до дальней планеты, годы | Период между оптимальными циклами, годы |
| Земля - Юпитер - Сатурн | 1976-78 | 12,2 - 14 | 3 - 5 | |
| Земля - Юпитер - Уран | 1978-79 | 12,7 - 14 | 6 - 9 | |
| Земля - Юпитер - Нептун | 1978-79 | 12, 7 - 14 | 8 - 14 | |
| Земля - Юпитер - Плутон | 1976-77 | 12,7 - 14 | 8 - 15 |
Логика работы программы SUNPL.EXE
Для получения квазиоптимальных траекторий при практических расчетах используют МЕТОДИКУ СФЕР ДЕЙСТВИЯ, сущность которой заключается в следующем. В некоторой окрестности притягивающего тела — его сфере действия — при расчете траектории движения КА учитывают только силу притяжения этого тела. Такое допущение позволяет считать траекторию движения КА в сфере действия невозмущенной и применять для ее определения аналитическую теорию задачи двух тел. В рамках этой методики все околосолнечное пространство можно назвать сферой действия Солнца, в которой планеты движутся в соответствии с законом всемирного тяготения. Так как планеты являются телами, обладающими конечной массой, то в некоторой окрестности планет сила их притяжения оказывается основной силой, действующей на КА. Значения сферы действия планет зависят от массы планеты и удаления ее от Солнца.
В итоге каждая планета как бы «вырезает» в сфере действия Солнца некоторую область, в которой сила ее притяжения является доминирующей. В силу этого все околосолнечное пространство можно представить в виде сфер действия планет, «погруженных» в сферу действия Солнца и перемещающихся вместе с планетами по их орбитам. Тогда траекторию движения КА при перелетах от планеты к планете можно рассматривать как траекторию, последовательно проходящую через несколько сфер действия, причем внутри каждой сферы действия траектория определяется начальными условиями на границе этой сферы и притяжением центрального тела.
Сферы действия даже самых массивных планет малы по сравнению со сферой действия Солнца. В силу этого на большей части межпланетной траектории движение КА зависит лишь от силы притяжения Солнца, и именно этот участок является определяющим при расчетах всей траектории перелета. Траекторию движения вблизи планет выбирают таким образом, чтобы при переходах от одной сферы действия к другой не нарушалась ее гладкость.
В соответствии с вышесказанным расчеты межпланетных траекторий проводят в следующей последовательности.
· Задают дату старта КА с орбиты Земли и время прилета КА к планете назначения. Это позволяет определить положение и скорости планет на их орбитах для моментов старта и прилета, а также время перелета КА от одной планеты к другой.
· Считая на первом этапе сферы действия планет бесконечно малыми, определяют параметры межпланетной орбиты в сфере действия Солнца. Для этого используют хорошо разработанные методы определения орбит, например метод Ламберта—Эйлера.
· Определив параметры орбиты, вычисляют гелиоцентрические скорости КА в момент отлета с орбиты планеты старта и в момент прилета к планете назначения.
· Зная гелиоцентрические скорости КА и планет в моменты старта и встречи, вычисляют скорость КА относительно планет как разницу соответствующих векторов. Эта скорость «на бесконечности» определяет избыток скорости КА относительно планеты на границе ее сферы действия, необходимый для вывода аппарата на выбранную межпланетную траекторию.
· По величине вектора скорости «на бесконечности» и его ориентации в пространстве определяют траекторию движения КА в сфере действия планет. Знание одного вектора скорости «на бесконечности» недостаточно для определения параметров планетоцентрической траектории. Поэтому необходимо задать дополнительные условия. При старте с Земли такими условиями являются параметры стартовой орбиты ИСЗ (например, наклонение и величина перигея орбиты), при подлете к планете — параметры пролета у планеты (в зависимости от принятой схемы полета).
· Зная параметры припланетных траекторий, определяют затраты характеристической скорости, необходимые для ее формирования.
|
|
|


