 |
Нахождение оптимальных параметров для полета тела через прямоугольную преграду
|
|
|
|
Выполнил: ученик 11 Б класса Назаркин Павел Дмитриевич
Муниципальное общеобразовательное учреждение «Лицей №43»
Саранск, 2004
Постановка задачи.
Произвести необходимые расчеты для нахождения минимальной скорости тела, брошенного через прямоугольное препятствие.
Методы выполнения работы.
Для выполнения данной работы проделаем ряд математических вычислений и преобразований с использованием физических формул.
Зная, что траекторией движения тела, является парабола, а также математическую формулу записи данной линии, будем использовать уравнение параболы общего вида в качестве начальных данных поставленной задачи. В выбранной нами прямоугольной системе координат запишем данное уравнение для двух точек, принадлежащих линии движения – начальной точке А и точке В, в которой тело окажется через некоторый промежуток времени t. Решая систему полученных при этом уравнений, путем математических замен и преобразований выведем формулу зависимости движения тела от одной переменной L, т.е. коэффициенты k и b, участвующие в общем виде уравнения параболы, выразим через L. Затем, используя физический закон движения тела, брошенного под углом к горизонту, выразим переменную L через 
и V. В результате получим уравнение движения, в качестве коэффициентов в котором будут выступать переменные и V. Затем составим систему двух уравнений, полученных подстановкой координат точек А и В в последнее уравнение движения. Решая данную систему, мы найдем неизвестные нам величины и V, выразив их через имеющиеся известные нам параметры – ширину и высоту прямоугольного препятствия. Для нахождения Vmin воспользуемся производной функции.
|
|
|
Решение.
Уравнением линии движения тела, брошенного через прямоугольное препятствие, в общем виде является уравнение параболы:
y=-kx2+b
Введем прямоугольную систему координат и свяжем ее с прямоугольным препятствием, как показано на рисунке.
В данной системе координат уравнение движения тела в точках А и Б примет вид:
0=-k(a+L)2+b,
h=-ka2+b.
Выразим k и b через одну неизвестную L:
Вычитаем 1)-ое из 2)-ого:
h=k(a2+2aL+L2-a2),
h=k(2aL+L2), 
(*);
h=b-ka2+b b=h+ka2 
. (*)
Получилось, что уравнение движения зависит только от L:
y=-kx2+b, где коэффициенты k и b имеют вид (*).
Найдем зависимость L от и V.
Из курса физики известно: что движение тела, брошенного под углом горизонта описывается уравнениями
x=Vxt L=Vxt L=Vcos t
y=Vyt+gt2/2 h=Vyt-gy t2/2 gt2-2Vyt+2h=0.
gt2-2Vyt+2h=0.
.
Мы рассматриваем время движения от точки А до Б, значит
, где Vy=Vsin .
Итак, 
Умножив обе части уравнения на g, получим:
(1)
Известно, что 
т.е. 
(2)
С другой стороны tg =y’ в точке А, т.е. tg =y’(-a-L);
Подставив значение tg в (2), получим:
V2sin2 =g(a+L) tg
V2sin cos =g(a+L) Lg=V2sin cos -ga (3)
Сравнив (1) и (3) получаем, что:
.
Получили уравнение с двумя неизвестными V и : выразив V через , мы получим ту самую функцию, которую мы должны были найти:
Пусть z=V2, тогда z cos2 (z sin2 -2gh)=g2a2;
z2 cos2 sin2 - z cos2 2gh-g2a2=0;
Получили квадратное уравнение относительно z
Очевидно, 
значит, т.к. z=V2>0, то 
.
Вместо зависимости V от рассмотрим зависимость z от , и обозначив 
получим зависимость z от t.
Получим 
, где z=V2, .
Выразим 
через t, если 
; 
Значит, 
Т.е. 
Таким образом, чтобы найти Vmin и , нам нужно во-первых, найти fmin и t.
.
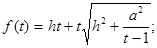
Умножив обе части уравнения на 
, получим
Прежде чем возвести обе части в квадрат, сделаем предварительный анализ получившегося уравнения: т.к. 
то и 
т.е. 
и 
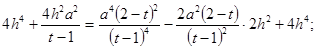
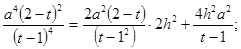
Умножив обе части уравнения на (t-1)2, получим
Т.к t<2 и t>1 (т.к. 
), то можно извлечь корень.
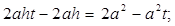
; (4)
Итак, f(t)=2h+2a, значит 
.
Т.к. z=V2, то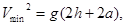 
т.е. 
(5)
Осталось найти L:
|
|
|
Его найдем используя (3).
Результаты работы.
Проделанным расчетом мы нашли зависимость скорости, движения брошенного через прямоугольное препятствие тела, так чтобы она была минимальной, от длины и высоты прямоугольного препятствия. То есть, зная данные препятствия, - его длину и ширину – а так же формулы, полученные в данной работе, мы можем определить на каком расстоянии от препятствия, под каким углом и с какой минимальной скоростью необходимо бросить тело, чтобы оно перелетело через это препятствие.
Актуальность темы.
Данные расчеты и выведенные формулы используются в различных сферах деятельности человека. В частности, в военной практике, для правильного расчета движения траектории снарядов.
Приложение.
К работе прилагается программа, результатом которой является вывод на экран траектории движения тела, брошенного через прямоугольное препятствие. Входными параметрами программы являются данные прямоугольного препятствия – его длина и высота. Программа написана на языке программирования Delphi.
|
|
|
