 |
Векторная алгебра и аналитическая геометрия в пространстве
|
|
|
|
Вектор – отрезок, имеющий определенную длину и направление. Любой вектор можно разложить по ортам координатных осей:
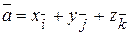 , где
, где
х, у, z – проекции вектора 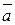 на оси координат,
на оси координат, 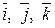 - орты (единичные векторы координатных осей).
- орты (единичные векторы координатных осей).
Модуль (длина) вектора 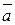 определяется по формуле:
определяется по формуле:
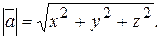 (3.1.1)
(3.1.1)
Если известны координаты начала 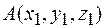 и конца В(
и конца В(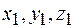 )вектора, то вектор
)вектора, то вектор 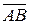 можно записать следующим образом:
можно записать следующим образом:
 (3.1.2)
(3.1.2)
Скалярным произведением двух ненулевых векторов 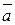 и
и 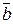 называется произведение их модулей на косинус угла между ними:
называется произведение их модулей на косинус угла между ними:
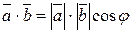 .
.
Отсюда нетрудно определить угол между векторами
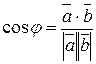 . (3.1.3)
. (3.1.3)
Если векторы  и
и 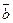 заданы своими проекциями
заданы своими проекциями 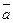 =
= 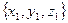 и
и 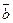 =
= 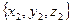 , то скалярное произведение находится по формуле:
, то скалярное произведение находится по формуле:
 . (3.1.4)
. (3.1.4)
Векторы ортогональны, если их скалярное произведение равно нулю, т.е.:
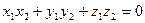 . (3.1.5)
. (3.1.5)
Векторным произведением двух векторов называется вектор 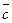 , определяемый условиями:
, определяемый условиями:
1) вектор 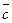 перпендикулярен векторам
перпендикулярен векторам  и
и 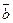 , т.е.
, т.е. 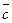
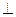
 ,
, 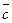
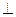
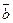 ;
;
2) векторы  ,
, 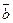 и
и 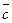 образуют правую тройку;
образуют правую тройку;
3) длина вектора 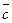 равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах  и
и 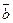 как на сторонах, т.е.
как на сторонах, т.е.
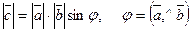 .
.
Для векторов, заданных проекциями 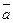 =
= 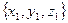 и
и 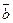 =
= 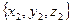 , векторное произведение имеет вид:
, векторное произведение имеет вид:
 . (3.1.6)
. (3.1.6)
Отсюда, условие коллинеарности векторов:
 . (3.1.7)
. (3.1.7)
Смешанным произведением трех векторов  ,
, 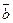 и
и 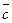 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 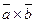 на вектор
на вектор 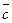 , т.е.:
, т.е.:
(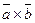 )
) 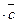 .
.
Геометрически модуль смешанного произведения равен объему параллелепипеда, построенного на векторах  ,
, 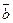 и
и 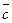 , как на ребрах.
, как на ребрах.
Если векторы заданы проекциями 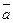 =
= 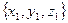 ,
, 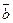 =
= 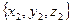 и
и 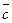 =
=  , то смешанное произведение имеет вид:
, то смешанное произведение имеет вид:
 . (3.1.8)
. (3.1.8)
Условие компланарности (принадлежности трех векторов одной плоскости или параллельности плоскостям), имеет вид:
 . (3.1.9)
. (3.1.9)
Знание векторной алгебры во многом упрощает решение задач по аналитической геометрии в пространстве.
|
|
|
Так, уравнение плоскости, проходящей через заданную точку М(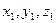 ), перпендикулярно вектору
), перпендикулярно вектору  имеет вид:
имеет вид:
 . (3.1.10)
. (3.1.10)
Уравнение плоскости, проходящей через три точки: А(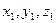 ), В(
), В(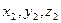 ), и С(
), и С(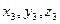 ), имеет вид:
), имеет вид:
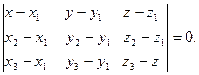 (3.1.11)
(3.1.11)
Канонические уравнения прямой в пространстве имеют вид:
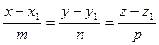 , (3.1.12)
, (3.1.12)
где (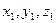 )-точка, через которую проходит прямая;
)-точка, через которую проходит прямая; 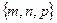 -проекции направляющего вектора прямой.
-проекции направляющего вектора прямой.
Уравнения прямой, проходящей через две точки, определяются так:
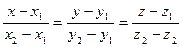 . (3.1.13)
. (3.1.13)
Если прямая вида (3.1.12) перпендикулярна плоскости, заданной общим уравнением: 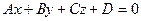 , то выполняется условие:
, то выполняется условие:
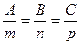 . (3.1.14)
. (3.1.14)
Рассмотрим несколько примеров применения изложенных выше теоретических положений.
Пример 6.
Записать вектор 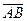 в системе орт и найти его модуль, если А(1, 2, 3);
в системе орт и найти его модуль, если А(1, 2, 3);
В(0, 1, 5).
Решение.
Используя формулу (3.1.2) получим:
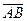 =(0-1)
=(0-1) 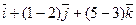 =
=  .
.
Используя формулу (3.1.1), найдем модуль этого вектора:
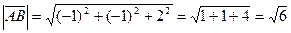 (ед.дл.)
(ед.дл.)
Пример 7.
Найти угол между векторами 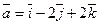 и
и 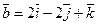 .
.
Решение.
Используя формулу (3.1.3), получим:
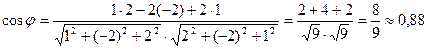 ,
,
что соответствует углу  .
.
Пример 8.
Найти площадь треугольника, образованного двумя векторами  и
и
 , выходящими из одной точки.
, выходящими из одной точки.
Решение.
Площадь треугольника, построенного на векторах  и
и 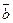 , равна половине площади параллелограмма, построенного на этих же векторах как на сторонах, т.е. равна
, равна половине площади параллелограмма, построенного на этих же векторах как на сторонах, т.е. равна  модуля векторного произведения векторов
модуля векторного произведения векторов  и
и 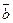 :
:
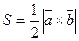 .
.
Векторное произведение найдем по формуле (3.1.6):
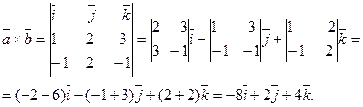
Найдем модуль полученного вектора, используя формулу (3.1.1):

Тогда искомая площадь будет:
 (кв.ед.)
(кв.ед.)
Пример 9.
Найти объем пирамиды, построенной на трех некомпланарных векторах:
 .
.
Решение:
Объем пирамиды, построенной на трех некомпланарных векторах как на ребрах, равен
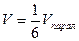 , где
, где  ,
,
где 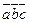 -смешанное произведение векторов.
-смешанное произведение векторов.
Величину 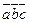 найдем по формуле (3.1.8):
найдем по формуле (3.1.8):
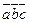 =
= 
Тогда 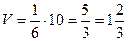 (куб.ед.).
(куб.ед.).
Пример 10.
Найти каноническое уравнение прямой, проходящей через две точки А(1,2,5) и В(0,1,2).
Решение:
Подставив координаты точек А и В в уравнение (3.1.13), получим:
|
|
|
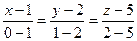 ;
; 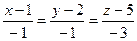 ;
; 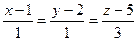 .
.
Пример 11.
Найти уравнение плоскости, проходящей через три точки: А(1, 2, 3);
В(1, 1, 0) и С(2, 3, 1).
Решение:
Используя уравнение (3.1.11), получим:
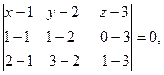
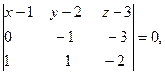
(х-1) 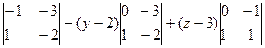 ,
,
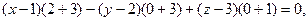
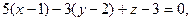
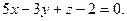
Пример 12.
Через точку А(1, 0, 2) провести прямую, перпендикулярную плоскости 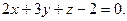
Решение.
Используем канонические уравнения прямой (3.1.12), подставив координаты точки А, получим:
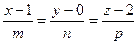 .
.
Проекции направляющего вектора прямой 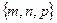 найдем из условия перпендикулярности прямой и плоскости (3.1.14).
найдем из условия перпендикулярности прямой и плоскости (3.1.14).
В нашем случае это будет: 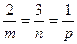 , тогда будем иметь:
, тогда будем иметь: 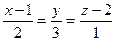 .
.
Вопросы для самопроверки
1. Что называется вектором?
2. Как найти проекции вектора, если известны координаты его начала и конца?
3. Что такое модуль вектора и как его найти?
4. Чему равно скалярное произведение векторов, заданных проекциями?
5. Как найти угол между векторами?
6. Чему равна площадь треугольника?
7. Чему равен объем пирамиды?
8. Напишите канонические уравнения прямой.
9. Как найти прямую, проходящую через две точки?
10. Как найти уравнение плоскости, проходящей через три точки?
11. Сформулируйте условие перпендикулярности прямой и плоскости.
Варианты индивидуальных заданий
Задание №1
Решить систему уравнений методами Крамера и Гаусса. Сделать проверку полученного решения.
1. 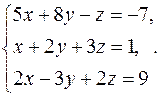 2.
2. 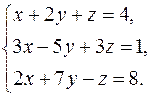
3. 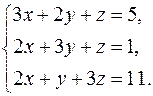 4.
4. 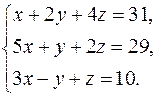
5. 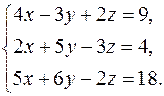 6.
6. 
7. 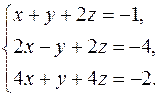 8.
8. 
9.  10.
10. 
11. 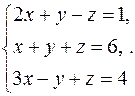 12.
12. 
13. 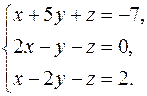 14.
14. 
15. 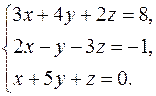 16.
16. 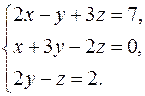
17. 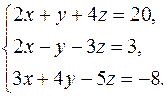 18.
18. 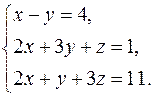
19. 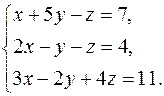 20.
20. 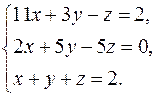
Задание №2
Даны координаты вершин треугольника АВС.
Найти:
1)длину стороны АВ;
2)уравнение стороны АВ и ее угловой коэффициент;
3)уравнение и длину высоты СД;
4)уравнение медианы АЕ;
5)уравнение прямой, проведенной через точку Е, параллельно стороне АВ;
6)сделать чертеж.
1. А(-5;0), В(7;9), С(5;-5). 11. А(-5;2), В(7;-7), С(5;7).
2. А(-7;2),В(5;11),С(3;-3). 12. А(-7;5), В(5;-4), С(3;10).
3. А(-5;-3), В(7;6), С(5;-8). 13. А(-7;1), В(5;-8), С(3;10).
4. А(-6;-2), В(6;7), С(4;-7). 14. А(0;3), В(12;-6), С(10;8).
5. А(-8;-4), В(4;5), С(2;-9). 15. А(-8;4), В(4;-5), С(2;9).
6. А(0;-1), В(12;8), С(10;-6). 16. А(-2;2), В(10;-7), С(8;7).
7. А(-6;1), В(6;10), С(4;-4). 17. А(1;2), В(13;-7), С(11;7).
8. А(-2;-4), В(10;5), С(8;-9). 18. А(-4;1), В(8;-8), С(6;6).
9. А(-3;0), В(9;9), С(7;-5). 19. А(-7;-1), В(5;-10), С(3;4).
10. А(-9;-2), В(3;7), С(1;-7). 20. А(-3;3), В(9;-6), С(7;8).
Задание №3
Даны координаты вершин пирамиды АВСД.
Найти:
1) векторы  в системе орт и их модули;
в системе орт и их модули;
2) угол между векторами 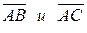 ;
;
3) площадь грани АВС;
|
|
|
4) объем пирамиды АВСД;
5) уравнение ребра АВ;
6) уравнение плоскости АВС;
7) уравнение высоты, опущенной из точки Д на плоскость АВС.
1. А(1;2;1), В(-1;5;1), С(-1;2;7), D(1;5;9).
2. А(2;3;2), В(0;6;2), С(0;3;8), D(2;6;10).
3. А(0;3;2), В(-2;6;2), С(-2;3;8), D(0;6;10).
4. А(2;1;2), В(0;4;2), С(0;1;8), D(2;4;10).
5. А(2;3;0), В(0;6;0), С(0;3;6), D(2;6;8).
6. А(2;2;1), В(0;5;1), С(0;2;7), D(2;5;9).
7. А(1;3;1), В(-1;6;1), С(-1;3;7), D(1;6;9).
8. А(1;2;2), В(-1;5;2), С(-1;2;8), D(1;5;10).
9. А(2;3;1), В(0;6;1), С(0;3;7), D(2;6;9).
10. А(2;2;2), В(0;5;2), С(0;2;8), D(2;5;10).
11. А(1;3;2), В(-1;6;2), С(-1;3;8), D(1;6;10).
12. А(0;1;2), В(-2;4;2), С(-2;1;8), D(0;4;10).
13. А(0;3;0), В(-2;6;0), С(-2;3;6), D(0;6;8).
14. А(2;1;0), В(0;4;0), С(0;1;6), D(2;4;8).
15. А(0;2;1), В(-2;5;1), С(-2;2;7), D(0;5;9).
16. А(1;1;1), В(-1;4;1), С(-1;1;7), D(1;4;9).
17. А(1;2;0), В(-1;5;0), С(-1;2;6), D(1;5;8).
18. А(0;1;0), В(-2;4;0), С(-2;1;6), D(0;4;8).
19. А(0;1;1), В(-2;4;1), С(-2;1;7), D(0;5;9).
20. А(0;2;0), В(-2;5;0), С(-2;2;6), D(0;5;8).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Письменный Д. Т.
Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. - 9-е изд. - М.: Айрис-Пресс, 2008. – 280с.- Ч. 1.
2. Пискунов Н. С.
Дифференциальное и интегральное исчисления: учеб. пособие для вузов / Н. С. Пискунов. - изд. стер.. - М.: Интеграл-Пресс, 2006. – 415 с. Т.1.
3. Шипачев В.С.
Курс высшей математики: учебник для вузов / В.С.Шипачев; Под редакцией А.Н. Тихонова. – 3-е изд., испр. – М.: Издательство Оникс, 2007 – 600с.: ил.
4. Берман Г. Н.
Сборник задач по курсу математического анализа: учеб. пособие / Г. Н. Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006 - 432 с.
5. Лунгу К.Н.
Сборник задач по высшей математике: учеб. пособие / К.Н.Лунгу и др.- 7-е изд..- М.: Айрис Пресс, 2008.- 574 с.
6. Шипачев В. С.
Задачник по высшей математике: учеб. пособие для вузов / В. С. Шипачев. - 8-е изд., стер. - М.: Высш. шк., 2008. - 304 с.: ил.
7. Данко П. Е.
Высшая математика в упражнениях и задачах: учеб. пособие / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд..-М.: ОНИКС.- 2008.-368 с.- Ч.1.
|
|
|


