Исходные данные и задания на курсовую работу

Каждый студент получает индивидуальное задание, которое содержит вариант исследуемой системы с исходными данными.

Задание на курсовую работу фиксируется в день выдачи на типовом бланке, подписывается студентом и руководителем и помещается впоследствии в пояснительную записку к курсовой работе. Ниже приводятся типовые варианты систем, исследуемых в курсовой работе.

Допускается выдача нетипового задания, удовлетворяющего тематике и требованиям к курсовой работе.

 

Цифровая управляющая система

Для управления некоторым объектом в реальном масштабе времени используется цифровая управляющая система (ЦУС). Сигналы о текущем состоянии объекта управления поступают в ЦУС и обрабатываются ЭВМ, входящей в состав ЦУС. ЭВМ вырабатывает управляющие сигналы, которые передаются на объект управления и изменяют его состояние.

В данном варинате ЦУС поступающие сигналы от объекта управления могут быть трех типов. Для каждого типа сигналов моменты времени их поступления образуют пуассоновский поток с интенсивностями λ₁, λ₂, λ₃ (соответственно для сигналов 1, 2 и 3-го типов). Обработка сигналов производится при помощи хранящихся в памяти ЭВМ прикладных программ П₁, П₂, П₃, средние трудоемкости которых составляют θ₁, θ₂, θ₃ машинных операций. Если через В опер./с обозначить быстродействие ЭВМ, то счет по программе П_i занимает в среднем θ_i/B с. Фактическое время обработки конкретного сигнала может оказаться и меньше и больше среднего значения. Предполагается,. что это время является случайной величиной Т с показательным законом распределения

P{ T_i>t } = exp(-αt), (A = В/θ_i; i = 1,2,3).

Сигналы, которые в момент поступления застают ЭВМ занятой обработкой предыдущих сигналов, накапливаются в специальном буферном регистре и обрабатываются по мере освобождения ЭВМ. Таким образом время реакции ЦУС на сигнал, вообще говоря, складывается из времени ожидания обработки и времени T_i самой обработки.

Время реакции системы на сигнал - это основная характеристика качества работы ЦУС, поскольку при реальном масштабе времени различные ситуации, возникающие в процессе функционирования объекта исследования (необходимость переключения режимов работы, отказы отдельных узлов и т.п.), требуют незамедлительного вмешательства устройства управления.

Требуется определить путем имитационного моделирования:

1) зависимость среднего времени реакции ЦУС на сигнал каждого типа от быстродействия ЭВМ;

2) зависимость средней загрузки ЭВМ отее быстродействия;

3) среднее время реакции на сигнал каждого типа, предполагая, что сигналы 1-го типа обрабатываются в первую очередь;

4) закон распределения случайной величины "количество сигналов, ожидающих разработки;

5) вероятность того, что время реакции ЦУС на сигнал превысит 0.2 с;

6) среднее время реакции системы на сигнал каждого типа в предположении, что при выборе сигнала на обработку сигналы 1 –го типа имеют самый высокий приоритет, а сигналы 3 - го типа – самый низкий.

 

Значения параметров:

B - в пунктах задания 1 и 2 изменяется от 50000 до 100000 опер./с с шагом 10000. Для пунктов задания 3.. 6 B = 60000. Остальные параметры берутся из табл. 3.1.

Таблица 3.1

Вариант	λ1	λ2	λ3	θ1	θ2	θ3
а	2,5	1,5
b	2,0	2,0

 

 

Список вариантов: 1а, 1в, 2а, 2в, 3а, 3в, 4а, 4в, 5а, 5в, 6а, 6в (12 вариантов).

 

Сеть телефонной связи

Рассматривается сеть телефонных линий, связывающих несколько городов. Схема сети приведена на рис.1. Каждая линия может иметь несколко каналов для ведения переговоров (т.е. по линии могут одновременно соединяться несколько пар абонентов). Количество каналов задается на схеме числом параллельных ребер, соединяющих концы линий.

В каждом городе может быть принят заказ на переговоры с любым другим городом. Предполагается, что моменты времени поступления заказов в городе i на переговоры с городом j образует пуассоновский поток с интенсивностью λ_ij, а продолжительность разговора считается случайной величиной с известным законом распределения.

При поступлении в городе i заказа на переговоры с городом j может оказаться, что немедленное соединение невозможно, так как все каналы, по которым i можно связать с j, заняты обслуживанием других переговоров. В этом случае заказ ожидает освобождения канала.

Требуется определить путем имитационного моделирования величины T_ij - среднее время ожидания разговора с городом j в городе i (i = 1,2,3,4; j = 1,2,3,4; i = j).

 

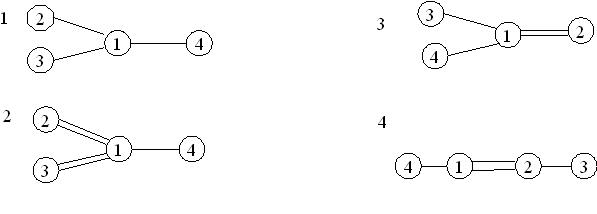
Рис.1. Варианты сетей связи

 

Варианты интенсивностей λ_ij заказов/ч приведены: g) в табл. 3.2; h) в табл. 3.3.

 

Таблица 3.2 Таблица 3.3

 

I	J
	-	1,8	1,2	0,6
	1.3	-	0,6	0.2
	0,8	0.8	-	0,2
	1,0	0,5	0,2	-

 

I	J
	-	2,0	1,5	0,8
	1.5	-	0,6	0.4
	1,0	0.9	-	0,3
	1,2	1,0	0,2	-

 

 

Варианты распределения продолжительности переговоров:

а) все равномерно распределены на промежутке времени от 3 до 7 мин;

б) имеет распределение на отрезке [3 мин, 7 мин]. Плотность распределения задается формулой

f(x) = (3/64) (x - 3)(7 - x)² (3 < x < 7).

 

Список вариантов: 1gа, 1gб, 1hа, 1hб, 2gа, 2gб, 2hа, 2hб, 3gа, 3gб, 3hа, 3hб, 4gа, 4gб, 4hа, 4hб, (16 вариантов).

 

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: