 |
Пример расчёта дифференциальной передачи.
|
|
|
|
Пусть дана дифференциальная передача, у которой известны числа зубцов всех колёс (рис. 9):
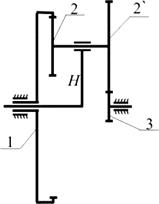
Рис. 9. Дифференциальная передача. Пример расчета.
z 1=80; z 2=20; z 2'=30; z 3=30; n 1=300 об/мин; nH =200 об/мин.
Требуется определить числа оборотов всех колёс передачи.
По формуле Виллиса: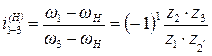 
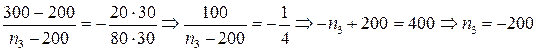об/мин.
Знак «–» перед значением n 3 соответствует случаю, когда направление вращения звена 4 противоположно направлению вращений звеньев 1 и H.
Далее определяем число оборотов звена 2:
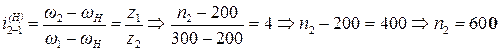об/мин,
n 2 = n 2’, так как z 2 и z 2’ жестко скреплены на одном валу.
Если в дифференциальной передаче ведущие звенья связать между собой дополнительной зубчатой передачей, то получится замкнутая дифференциальная передача.
Дифференциальная замкнутая передача
Замкнутая дифференциальная передача имеет одно ведущее звено (подвижность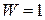 
) и подвижные центральные колёса.
В качестве примера рассмотрим дифференциальную передачу, (рис. 10, а) в которой два ведущих звена 1 и H. Если эти звенья замкнуть рядом колёс 1 `, 5 `, 5, 4, то получится замкнутая дифференциальная передача (рис. 10, б).
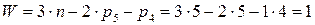
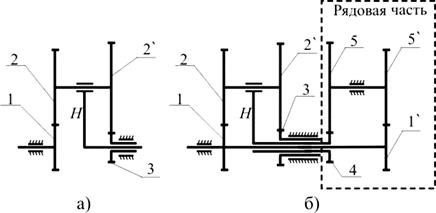
Рис. 10 Получение дифференциальной замкнутой передачи
Обычно для кинематического исследования таких передач составляется система двух алгебраических уравнений. Одно из них – уравнение для определения передаточного отношения от ведущего звена к ведомому звену дифференциальной части с помощью формулы Виллиса. Второе уравнение – уравнение замкнутости для определения передаточного отношения рядовой части передачи.
В результате решения полученной системы определяются угловые скорости всех звеньев, и соответственно, передаточное отношение механизма.
Для случая на рис. 10, б принимаем за ведущее звено 1. Система уравнений записывается в виде:
|
|
|
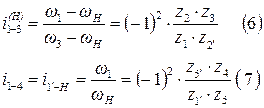
Числитель и знаменатель левой части уравнения (6) делим на w1:
,
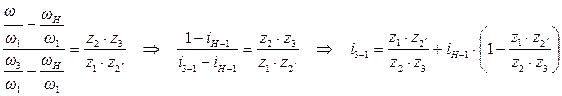используя (7), получаем
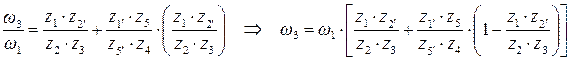
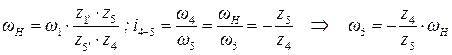
Для определения угловых скоростей сателлитов используем методику из предыдущего примера:
.
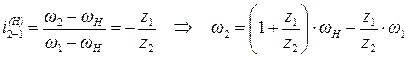Планетарные передачи
Планетарный механизм, у которого одно из центральных колёс закреплено неподвижно, называется планетарной передачей. Неподвижное центральное колесо называют опорным. Например, если в дифференциальной передаче (рис. 10) центральное колесо 3 жестко соединить со стойкой, то получится планетарная передача с одной степенью подвижности (рис. 11).
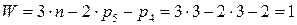
Следовательно, задавая движение центрального колеса 1, получают значение угловой скорости водила H. Если же задана w H, то можно определить w1.
Планетарные передачи применяют для получения значительных передаточных отношений, повышенных значений КПД при габаритах меньше, чем габариты рядовых передач.
Рис. 11. Планетарная передача.
Для вывода формулы передаточного отношения в планетарной передаче (рис. 11) применяется формула Виллиса:
,
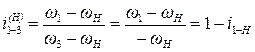так как w3=0.
Следовательно,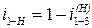 
при ведущем колесе 1. 
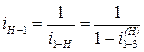при ведущем поводке H.
– передаточное отношение обращенного движения при неподвижном поводке и раскреплённом колесе 3: 
.
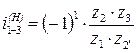В общем случае для планетарных передач:
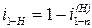, (8)
где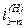 
– передаточное отношение от подвижного колеса 1 к неподвижному центральному колесу n при остановленном поводке H.
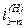определяется по соотношениям (8) для рядовых передач.
Смешанные передачи
Передачи, состоящие из рядовых и планетарных механизмов, называются смешанными или комбинированными. Порядок расчёта таких передач следующий:
1. Вся передача разделяется на отдельные простейшие виды известных передач по принципу: выходное звено предыдущей является входным для последующей ступени.
2. Подсчитываются передаточные отношения выделенных механизмов.
|
|
|
3. Общее передаточное отношение всего смешанного соединения равно произведению отдельных передаточных отношений из п. 2.
4. Определение угловых скоростей центральных колёс и сателлитов основано на методиках, изложенных в предыдущих разделах.
В качестве иллюстраций рассмотрим ряд примеров.
Пример 1. Определить передаточное отношение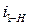 
редуктора (рис. 12).
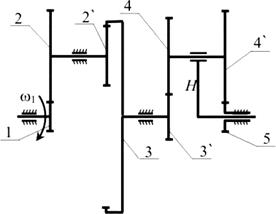
Рис. 12. Схема редуктора.
Решение.
а) Расчленяем смешанное соединение на рядовую передачу с кратным зацеплением (1,2,2`,3) и на планетарную передачу (3`,4,4`,5, H);
б)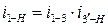 
;
в)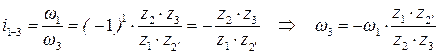 
;
г)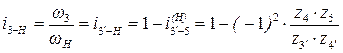 
;
д)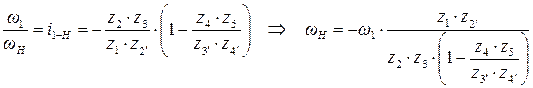 
;
е) Для нахождения угловой скорости сателлитов:
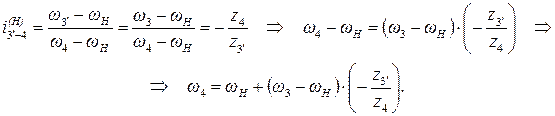
Пример 2. Определить передаточное отношение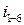 
редуктора (рис. 13).
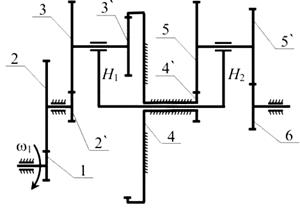
Рис. 13. Схема редуктора.
Решение.
а) Выделяем элементарные передачи: (1,2); (2`,3,3`,4, H 1); (H 2, 4`,5, 5`,6);
б)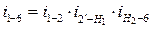 
;
в)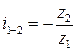 
;
г)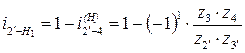 
;
д)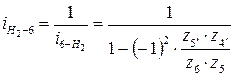 
;
е)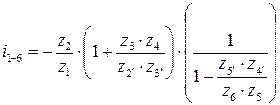 
;
ж) Чтобы, например, найти угловую скорость сателлитов 3 – 3` воспользуемся формулой:
,
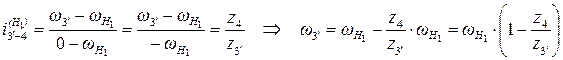где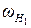 
можно определить из пункта г).
Пример 3. Определить передаточное отношение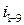 
, w4, w5 редуктора (рис. 14).
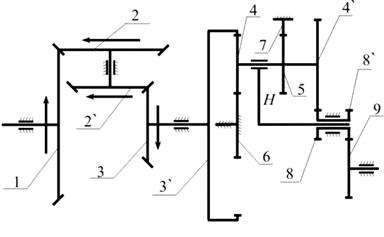
Рис. 14. Схема редуктора.
Решение.
а) Выделяем следующие ступени: рядовую передачу 1,2,2`,3; планетарную передачу 3`,4,6, H; планетарную передачу H,5,7,4`,8; рядовую передачу 8`,9;
б)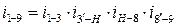 
;
в)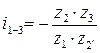 
(знак «–» выбран в соответствии с правилом стрелок);
г)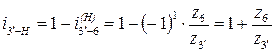 
;
д) 
;
е)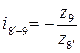 
;
ж)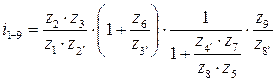 
;
з) При ведущем колее 1 из пунктов в) и г) находим:
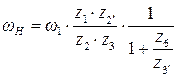; далее, 
,
.
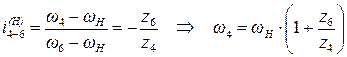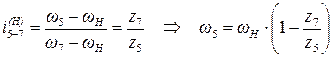Пример 4. Определить по исходным данным количество зубьев 9-го и 10-го колёс механизма (рис. 15).
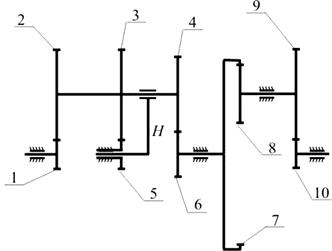
Рис. 15. Схема редуктора
Дано: z 1=20; z 2=60; z 3 =20; z 4 =15; z 5 =60; z 6 =65; z 7=78; z 8=24; n 1=3200 об/мин; n 10=200 об/мин.
Решение.
а)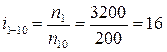 
;
б)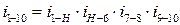 
,
;
в)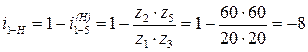 
;
г)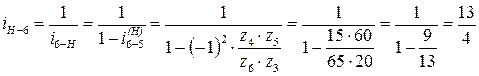 
;
д) 
,
;
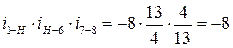е)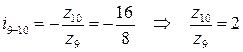 
;
ж) Из условия соосности всего механизма:
;
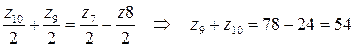з)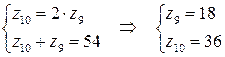 
.
Порядок выполнения работы
1. Составить кинематическую схему исследуемого зубчатого механизма. Если схема известна, то перейти к пункту 2.
2. Определить степень подвижности и вид механизма.
3. В зависимости от условия задачи сформировать значения исходных данных: числа зубьев колёс, модуль, угловые скорости ведущих звеньев и т.п.
4. Составить алгоритм подсчёта передаточного отношения соединения.
5. Провести расчёты.
6. Если необходимо, то определить значения угловых скоростей всех звеньев механизма, задав численное значение угловой скорости ведущего звена.
7. Для натурного механизма проверить правильность полученного передаточного отношения путём отметки относительного направления вращения ведущего и ведомого звеньев и замера чисел оборотов.
|
|
|
8. Сделать выводы по результатам работы.
5. Варианты расчётных заданий
| № Ва-ри-анта | Кинематическая схема | Условия |
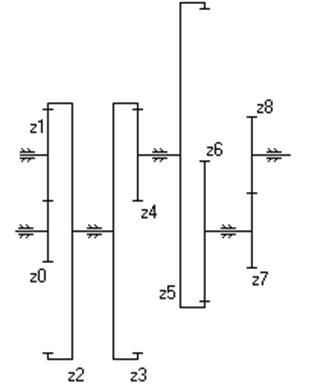
| Дано: z 0=20, z 1=30, z 2=100, z 3=100, z 4=30, z 5=90, z 6=20, z 7=30, z 8=10, w0=55 с-1. Найти: i 0-8, w1, w8. | |
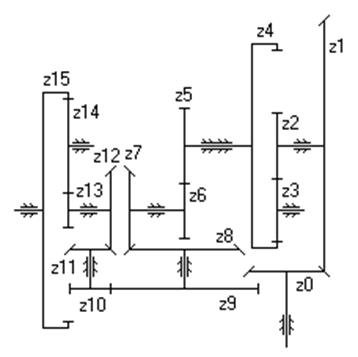
| Дано: z 0=20, z 1=56, z 2=22, z 3=18, z 4=68, z 5=24, z 6=24, z 7=40, z 8=44, z 9=64, z 10=22, z 11=28, z 12=40, z 13=20, z 14=18, z 15=102, n 0=900 об/мин. Найти: i 0-15, n 15, n 5, n 9. | |
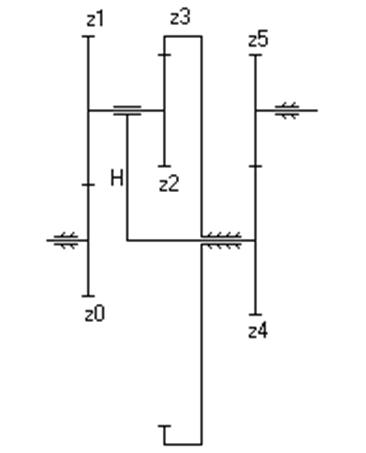
| Дано: z 0=20, z 1=40, z 2=35, z 3=70, z 4=15, z 5=30, n 5=115 об/мин. Найти: n 1, n 4. | |
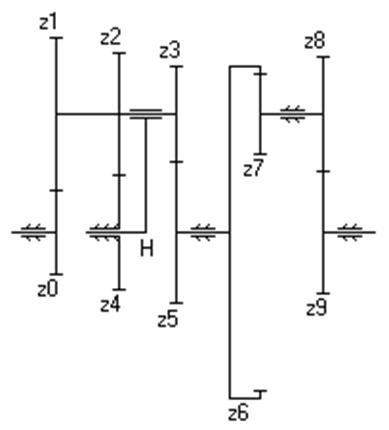
| Дано: z 0=20, z 1=60, z 2=20, z 3=15, z 4=60, z 5=65, z 6=78, z 7=24, m 8-9=6, n 0=3200 об/мин, n 9=200 об/мин. Найти: межосевое расстояние между 8 и 9 колёсами. | |
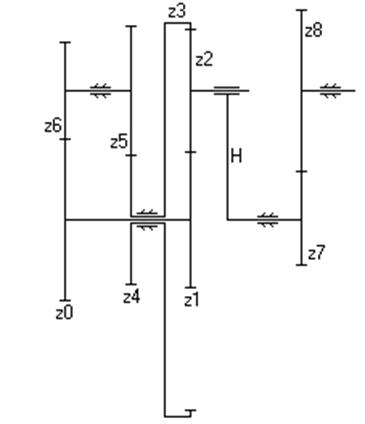
| Дано: z 0=24, z 1=24, z 2=28, z 3=80, z 4=28, z 4=26, z 5=30, z 6=12, z 7=28, n 8=250 об/мин. Найти: n 0. | |
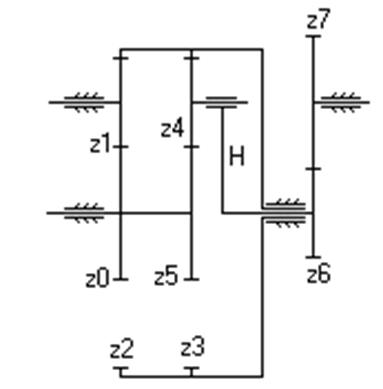
| Дано: z 0=20, z 1=22, z 2=80, z 3=80, z 4=18, z 5=30, z 6=30, z 7=18, n 0=650 об/мин. Найти: i 0-7, n 4. | |
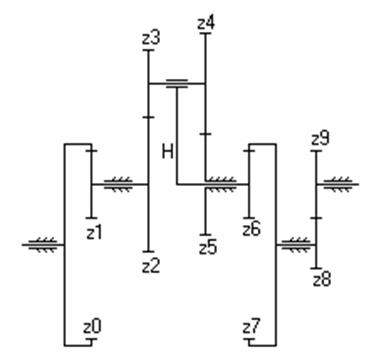
| Дано: z 0=80, z 1=30, z 2=40, z 3=28, z 4=24, z 5=42, z 6=40, z 7=80, z 8=28, z 9=40, w0=10 с-1. Найти: i 0-9, w3, w5. | |
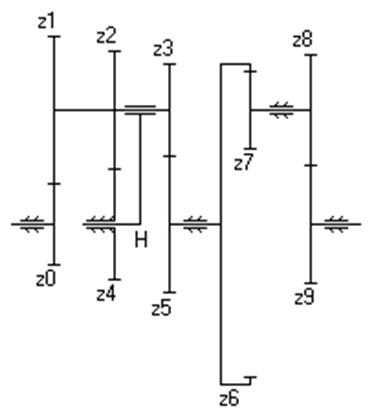
| Дано: z 0=20, z 1=60, z 2 =20, z 3=15, z 4 =60, Z 5 =65, z 6 =78, z 7 =24, n 0=3200 об/мин, n 9=200 об/мин. Найти: z 8 и z 9. | |
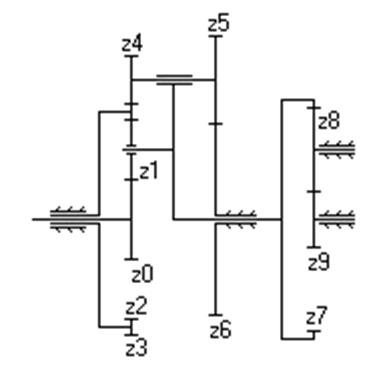
| Дано: z 0=20, z 1=17, z 2=57, z 3=80, z 4=25, z 5=20, z 6=85, z 7=90, z 8=14, z 9=61, n 0=900 об/мин. Найти: i 0-9, n 1, n 5. | |
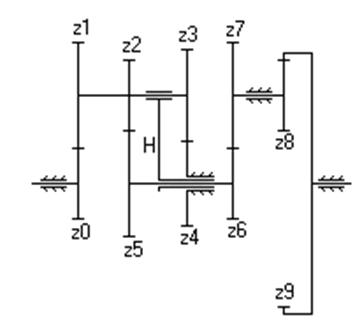
| Дано: z 0=20, z 1=40, z 2=30, z 3=34, z 4=30, z 5=34, z 6=28, z 7=40, z 8=20, z 9=70, n 0=300 об/мин. Найти: i 0-9, n 1. |
Литература
1. Теория механизмов и механика машин: учебник для вузов / К.В. Фролов [и др.]; МГТУ им. Н. Э. Баумана; Под ред. К.В. Фролова.— 5-е изд., стер.— М.: Изд-во МГТУ им. Н. Э. Баумана, 2004.— 662 с.
2. И. И. Артоболевский. Теория механизмов и машин. М., 1988.
3. И. И. Артоболевский, Б. В. Эдельштейн. Сборник задач по теории механизмов и машин. М., 1973.
|
|
|
