Способ перемены плоскостей проекций

Методические указания

К выполнению РГЗ № 1

«КОМПЛЕКСНАЯ ЗАДАЧА»

По начертательной геометрии

для студентов, обучающихся по направлению

Технология продукции и организация общественного питания»,

Продукты питания животного происхождения»

дневной формы обучения

Составитель: Червоняк Тамара Федоровна, старший преподаватель кафедры инженерной графики

 

 

Методические указания к выполнению графических работ рассмотрены и одобрены на заседании кафедры инженерной графики.

2011 года, протокол №

 

Рецензент:

Шамрина О.П. – доцент кафедры инженерной графики МГТУ

Оглавление

1. Введение

2. Методические указания к выполнению графической работы.

3. Перечень используемой литературы

4. Приложение 1. Пример выполнения работы.

Введение

 

В данных методических указаниях приведены краткие теоретические сведения по методам преобразования комплексного чертежа. Даны методические указания по решению метрических задач, которые решаются с помощью введения дополнительной плоскости, вращением вокруг проецирующей оси и плоскопараллельным перемещением.

Методические указания могут быть использованы студентами при подготовке к выполнению домашних заданий, графических работ, а также к контрольным работам и экзаменам.

Также приведены примеры решения некоторых основных задач и комплексной задачи РГЗ №1.

 

Методические указания к РГЗ

Комплексная задача «Пирамида»

Условие РГЗ:

Работа выполняется на листах формата А3 с основной надписью по ф.1. Чертеж выполняется простыми карандашами: для тонких линий - твердыми, для толстых – мягкими. Для выделения ответов можно использовать цветные карандаши. Нельзя использовать фломастеры и цветные ручки.

1. По заданным координатам построить пирамиду ABCS и определить видимость ребер.

2. Графическими построениями определить площадь основания пирамиды ABC.

3. Из вершины пирамиды S опустить перпендикуляр на основание ABC и найти истинную величину этого перпендикуляра.

4. Через точку S провести плоскость Q, перпендикулярную плоскости G, заданной треугольником ABC.

5. Определить величину двугранного угла при ребре BC.

 

Таблица 1.Координаты вершин пирамиды.

Вариант

A

B

C

S

x

y

z

x

y

z

x

y

z

x

y

z

Прежде чем приступать к решению задачи, внимательно прочитать и изучить тему «Методы преобразования чертежа», разобрать приведенные в методических указаниях примеры решения задач.

Способы преобразования чертежа

Общая характеристика способов преобразования чертежа.

Многие задачи решаются легко и просто, если прямые линии, плоскости (основания, грани, ребра, оси) геометрических тел находятся в частном положении. Такое частное, выгодное расположение геометрического элемента и плоскостей проекций может быть обеспечено преобразованием чертежа.

Рассмотрим два основных способа преобразования чертежа прямой линии или плоскости общего положения в чертеж с их частным положением. Они заключаются в следующем:

в одном случае – заменяют данную систему плоскостей проекций на новую так, чтобы в ней исходные объекты оказались в частном положении, не меняя своего расположения в пространстве;

в другом случае – изменяют положение исходных объектов в пространстве так, чтобы они приняли частное положение относительно неизменных плоскостей проекций.

В первом случае преобразование называют способом перемены плоскостей проекций, во втором – способом вращения.

Способ перемены плоскостей проекций

Этот способ широко применяется в машиностроении и приборостроении. Сущность способа перемены плоскостей проекций заключается в следующем: положение точек, линий, плоских фигур, поверхностей в пространстве не меняется, а система плоскостей проекций П', П", П'" дополняется плоскостями, образующими с П' или П", или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.

Каждая новая система выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла наиболее выгодное положение для выполнения требуемого построения.

На рис. 1 показано преобразование проекций точки А из системы П'/ П" в систему П'/ П^IV в которой вместо плоскости П" введена новая фронтальная плоскость П^IV, а плоскость П^I осталась неизменной. При этом П'┴ П^IV. В системе П'/ П^IV горизонтальная проекция точки А - А' – осталась неизменной. Проекция точки А на плоскости П^IV - А^IV – находится от плоскости П' на том же расстоянии, что и проекция точки А - А" на плоскости П". Это условие позволяет легко строить проекции на новой плоскости проекций. Для этого в новой системе плоскостей П'/ П^IV из проекции точки А' проводим на новую плоскость П^IV линию связи, перпендикулярную новой оси Х₁. На этой линии связи отмечают расстояние от оси Х₁ до новой проекции А^IV, равное расстоянию от оси Х до проекции А" (рис. 2).

 

 

Рис. 1

 

 

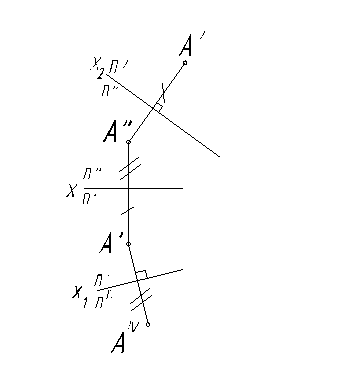
Рис. 2

 

При введении новой плоскости проекций, перпендикулярной фронтальной плоскости (система П''/П^V), расстояние откладывается по линии связи от оси Х₂ до новой проекции точки А^V, равное расстоянию от проекции А' до оси Х₁ (рис. 2).

Замену плоскостей проекций можно производить последовательно несколько раз.

 

Основные задачи пре­образования.

Определение вели­чины отрезка АВ общего положения показано на рисунке 3. Для этого фронтальная плоскость П" заменена на новую фронтальную плос­кость проекций П^IV, параллельную отрезку АВ (ось Х₁ параллельна горизонтальной проекции А'В'). Расстояния от оси Х₁ до А^IV и В^IV соответственно равны расстояниям от А" и В" до оси Х. Одновременно с определением натуральной величины отрезка определена величина α угла наклона отрезка АВ к плоскости П'.

Если ввести новую горизонтальную плоскость проекций П^V┴П" параллельно фронтальной плоскости проекций, отложив расстояния от оси Х₂ до А^V и В^V соответственно равные расстояниям от А' и В' до оси Х, то получим натуральную величину отрезка АВ и величину β угла наклона отрезка АВ к фронтальной плоскости П".

Рис. 3

Приведение отрезка прямой общего положения в проеци­рующее положение (рис.4). Сначала вводится новая плоскость проекций (например, П^IV_┴ П'), параллельно отрезку АВ (Х₁║А'В'). АВ находится в частном положении (уровня), затем вводится еще одна плоскость про­екций П^V, перпендикулярную плоскости проекций П^IV и отрезку АВ (А^IVВ^IV), ось проекций Х₂ перпендикулярна проекции А^IVВ^IV. Относительно этой плоскости проекций отрезок АВ занимает проецирующее положение: проекции А^V и В^V совпадают.

 

 

Рис. 4

Таким образом, для преобразования проекций отрезка общего положения на чертеже в проецирующее положение требуется введение двух новых плоскостей проекций последовательно: первой — парал­лельно отрезку, второй — перпендикулярно ему с условием перпендикулярности между исходными и новыми плоскостями проекций.

Приведение плоской фигуры общего положения в проецирующее положение. Решение основывается на предыдущей задаче. По­строение выполняют с помощью одной из линий частного поло­жения, например горизонтали А-1 с проекциями А'-1', и А"-1" (рис. 5). Новая плоскость проекций П^IV (П^IV_┴П') в этом случае выбрана перпенди­кулярно горизонтали A1 (ось Х₁ перпендикулярна горизонтальной проекции горизонтали А'-1').

Таким образом, заданная плоскость ΔАВС преобразована из общего положения во фронтально-проецирующее положение.

Аналогичным образом можно привести плоскость ΔАВС в горизонтально-проецирующее положение, если ввести новую горизонтальную плоскость перпендикулярно фронтальной проекции фронтали (П^IV _┴ П"; Х_{1 ┴} С"-2")(рис. 6).

 

 

Рис. 5

 

 

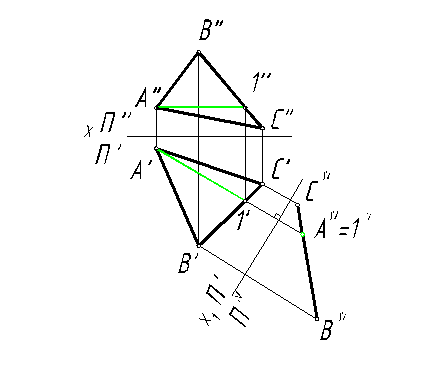
Рис. 6

 

Определение натурального вида плоской фигуры, расположенной в проецирующем положении (рис. 7).

 

 

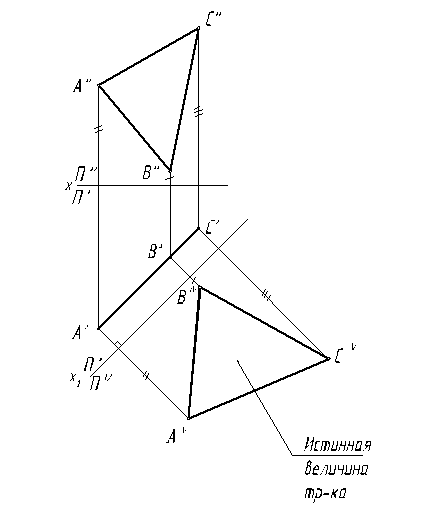
Рис. 7

 

Построение выполнено путем введения новой плоскости проекций П^IV, перпендикуляр­ной плоскости П', параллельной плоскости треугольника АВС (А'В'С'), при этом новая ось Х₁ параллельна проекции А'В'С'. Проекция плоскости треугольника А^IVВ^IVС ^IVявляется натуральной величиной задан­ного треугольника.

Следовательно, последовательным введением двух новых плоскостей проекций могут быть определены: натуральный вид плоской фигуры, принадлежащей плоскости общего положе­ния, и углы наклона плоскости к плоскостям проекций (рис. 8).

 

Рис. 8

 

 

Последовательность построения:

 

1. Находим в плоскости треугольника АВС горизонталь А-1 (А"-1", А'-1').

2. Вводим новую плоскость П^IV_┴ П' и перпендикулярно горизонтали плоскости треугольника (Х_{1 ┴} А'-1').

3. На новой плоскости П^IV строим проекцию треугольника А^IVВ^IVС^IV, используя координаты Z для каждой точки, взятые с плоскости П" до оси Х. Плоскость АВС на новой плоскости проекций занимает фронтально-проецирующее положение.

4. Вводим еще одну плоскость П^V_┴П^IV и параллельную плоскости треугольника (Х₂ ║ А^IVВ^IVС^IV).

5. На новой плоскости П^V строим проекцию треугольника А^VВ^VС^V, используя координаты Y для каждой точки, взятые с плоскости П' до оси Х₁. Плоскость АВС на новой плоскости проекций занимает горизонтальное положение уровня, а, следовательно, проецируется в истинную величину.

 

Определение величины двугранного угла.

Величина двугранного угла определяется линейным углом, составленным двумя перпендикулярами, проведенными на разных плоскостях к одной точке на ребре двугранного угла (рис. 9).

 

Рис. 9

Следовательно, для определения величины двугранного угла необходимо провести преобразование положения двугранного угла так, чтобы ребро двугранного угла и его грани заняли проецирующее положение (рис. 10,11 и 12).

 

Рис. 10 Рис. 11
На рисунке 10 ребро BD двугранного угла находится в горизонтально-проецирующем положении (BD_┴П', B"D"_┴Х), следовательно, двугранный угол проецируется на горизонтальную плоскость проекций в истинную величину.

На рисунке 11 ребро BD двугранного угла находится в горизонтальном положении уровня (BD_┴П', B"D"||Х), следовательно, чтобы расположить ребро перпендикулярно плоскости проекций нужно ввести новую фронтальную плоскость проекций П^IV_┴П' и чтобы она была перпендикулярна ребру BD (Х_1┴ B'D'). На новой плоскости проекций П^IV двугранный угол проецируется в истинную величину.

 

Рис. 12

 

На рисунке 12 выполнено двойное преобразование:

 

1. Вводим новую плоскость П^IV_┴ П' и параллельно ребру двугранного угла (Х₁ || B'D').

2. На новой плоскости П^IV строим проекцию двугранного угла А^IVВ^IVD^IVС^IV, используя координаты Z для каждой точки, взятые с плоскости П" до оси Х. двугранный угол АВDС на новой плоскости проекций занимает горизонтальное положение уровня.

3. Вводим еще одну плоскость П^V_┴П^IV и перпендикулярно ребру двугранного угла BD (Х_{2 ┴} B^IVD^IV).

4. На новой плоскости П^V строим проекцию двугранного угла А^VВ^VD^VС^V, используя координаты Y для каждой точки, взятые с плоскости П' до оси Х1. Двугранный угол АВDС на новой плоскости проекций занимает проецирующее положение, а, следовательно, проецируется в истинную величину.

 

 

Определение расстояния от точки до плоскости

Расстояние от точки до плоскости определяется истинной величиной отрезка, измеряемого по перпендикуляру от заданной точки до точки пересечения перпендикуляра с плоскостью.

Рис. 13

На рис.13 выполнено построение определения расстояния от точки до плоскости, находящейся в горизонтально-проецирующем положении.

Последовательность построения:

1. В заданной плоскости треугольника АВС определяем фронталь В-1 (В"-1", В'-1') и горизонталь А-2 (А"-2", А'-2').

2. Проводим горизонтальную проекцию перпендикуляра из точки S (S') перпендикулярно горизонтальной проекции горизонтали А-2 (А'-2'). Перпендикуляр пересечет плоскость треугольника АВС (его горизонтальную проекцию А'В'С') в точке К (К').

3. Проводим фронтальную проекцию перпендикуляра из точки S (S'') перпендикулярно фронтальной проекции фронтали В-1 (В''-1''). Точку пересечения перпендикуляра с плоскостью - К (К'') - находим по проекционной связи на фронтальной проекции перпендикуляра.

4. Отрезок SK является отрезком горизонтальной прямой уровня, а, следовательно, на горизонтальной плоскости проекций проекция S'K'=│SK│.

В случае если плоскость занимает общее положение, то для определения расстояния от точки до плоскости необходимо выполнить преобразование чертежа, чтобы привести плоскость в частное положение.

 

Для защиты графической работы необходимо ответить на следующие вопросы:

1. Какие способы преобразования чертежа рассмотрены в данной? В чем заключается их основное различие?

2. В чем заключается способ, называемый способом перемены плос­костей проекций?

3. Какие координаты точек остаются неизменными при замене горизонтальной (фронтальной) плоскости проекций?

4. Какие положения в системе П'/П" должна занять плоскость проек­ций П^IV, вводимая для образования системы П'/ П^IV

5. Как найти длину отрезка прямой общего положения и углы наклона этой прямой к плоскостям П' и П", вводя дополнительные плоско­сти проекции?

6. Как надо располагать новые плоскости проекций, чтобы отрезок прямой общего положения спроецировался в натуральную величину? в точку?

7. Сколько дополнительных плоскостей надо ввести в систему П'/П", чтобы определить натуральный вид фигуры, плоскость которой перпендикулярна к плоскости П' или к плоскости П"?

8. Как расположить новую плоскость проекций, чтобы заданная плоскость стала
проецирующей?

9. Сколько и в какой последовательности надо ввести дополнительных плоскостей в систему П'/П", чтобы заданная прямая общего поло­жения оказалась перпендикулярной к дополнительной плоско­сти проекций?

10. Сколько (и в какой последовательности) надо ввести дополнитель­ных плоскостей проекций в систему П'/П", чтобы получить нату­ральный вид фигуры, плоскость которой является плоскостью общего положения?

11. Как расположить новую плоскость проекций, чтобы заданная плоскость стала проецирующей?

12. При каком расположении треугольника можно определить натуральную величину с помощью замены только одной плоскости проекций?

13. В каком случае двугранный угол между плоскостями спроецируется на плоскость проекций в натуральную величину?

14. Сколько (и в какой последовательности) надо ввести дополнитель­ных плоскостей проекций в систему П'/П", чтобы получить нату­ральный вид двугранного угла, ребро которого является прямой общего положения?

 

Поделиться:

Воспользуйтесь поиском по сайту: