 |
Пересечение кривой поверхности плоскостью
|
|
|
|
Содержание эпюра. Даны кривая поверхность (конус) и проецирующая плоскость, требуется:
задача 1 – построить линию пересечения кривой поверхности с плоскостью;
задача 2 – определить действительную величину сечения;
задача 3 – построить наглядное изображение усечённой части кривой поверхности в прямоугольной изометрической аксонометрии.
Указания к выполнению эпюра. Данные берут из Приложения (задания к эпюру № 3).
ПОЯСНЕНИЯ К ВЫПОЛНЕНИЮ ЭПЮРА №3
Задача 1
В первой задаче эпюра №3 необходимо построить линию пересечения кривой поверхности, представленной конусом, с плоскостью, которая является фронтально-проецирующей.
Этап 1 (рис.19). Необходимо провести секущие плоскости во фронтальной плоскости проекций параллельно горизонтальной плоскости проекций (a, b, j). На горизонтальной плоскости проекций построим окружности, взяв за радиусы расстояния (на фронтальной плоскости проекций) от оси конуса до точек пересечения секущих плоскостей с образующими конуса (стороны S2C2 и S2D2). Как образец показан радиус R1. Найдем первую точку сечения. Это точка 12, которая лежит на образующей S2C2. Опустим проекционную связь на горизонтальную проекцию конуса и найдем точку 11, которая лежит на проекции образующей S1C1.
Рис. 19. Этап 1
Следующие точки, которые также легко находятся, лежат на окружности основания конуса – 22 и 32 (на фронтальной проекции они совпадают). Используя проекционную связь, находим их горизонтальные проекции (21 и 31) на окружности основания конуса.
Таким же образом найдем точки 42 и 52; 62 и 72; 82 и 92 и их горизонтальные проекции 41 и 51; 61 и 71; 81 и 91.
Рис. 20. Этап 2
Этап 2 (рис.20). На данном этапе необходимо соединить найденные точки сечения на горизонтальной проекции конуса.
|
|
|
Задача 2
Используя метод замены плоскостей проекций, найдем натуральную величину сечения. Для этого, параллельно заданной плоскости g2, на любом расстоянии проводим плоскость П5. На фронтальной плоскости проекций из точек сечения проводим линии связи перпендикулярно плоскости g2. На первой линии связи откладываем расстояние а, равное расстоянию от оси Х до точки 11. Все остальные точки сечения находятся аналогичным путем (см. рис. 20). По найденным точкам строим сечение и наносим штриховку. Построенное сечение является действительной величиной искомого сечения.
Задача 3
В задаче 3 необходимо построить наглядное изображение усечённой части кривой поверхности в прямоугольной изометрической аксонометрии.
Этап 3 (рис.21, рис. 22). Построение конуса в изометрии начинаем с построения основания. Окружность в изометрии превращается в эллипс (см. рис. 21). Эллипс строится в ромбе со сторонами (d), равными диаметру основания конуса.
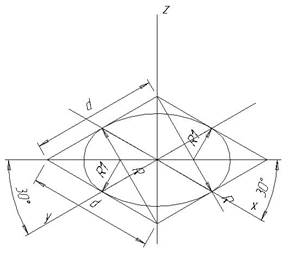Для того, чтобы сечение было более наглядным, поменяем местами оси Х и У. Для построения точек сечения необходимо использовать горизонтальную проекцию конуса.
Рис. 21. Этап 3 (1)
На рис. 22 показано построение проекций точек, лежащих в основании конуса.
Рис. 22. Этап 3 (2)
Этап 4 (рис. 23). На этом этапе в аксонометрической проекции нужно построить высоты проекций точек, лежащих в основании конуса. Для этого используется чертеж фронтальной проекции конуса. Каждая точка поднимается по своей высоте на проекционной связи, согласно ее высоте на фронтальной проекции (см. рис.23).
Рис. 23. Этап 4
Полученные точки (1,2,3,4.5,6,7,8,9) соединяются плавной линией. В заключение работы определяются видимые участки сечения. Пример выполнения эпюра №3 представлен на рис. 24.
|
|
|
Рис. 24. Пример выполнения эпюра №3
ЭПЮР №4
|
|
|
