 |
Теорема Безу. Корни многочлена и их кратность. Основная теорема алгебры.
|
|
|
|
Лекция 3
Раздел 2. Многочлены.
Сложение, умножение и алгоритм деления многочленов с остатком.
Определение. Алгебраическим многочленом степени п называется функция 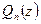 вида
вида
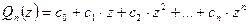 (1)
(1)
у которой  ‑ переменное комплексное число, а
‑ переменное комплексное число, а  ‑ постоянные комплексные числа, последнее из которых
‑ постоянные комплексные числа, последнее из которых  .
.
Числа  называют коэффициентами многочлена.
называют коэффициентами многочлена.
Для сокращенного обозначения многочленов обычно употребляют записи:
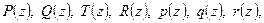
при этом, если хотят подчеркнуть, что многочлен  ‑ степени п, то пишут
‑ степени п, то пишут  .
.
Для нахождения суммы многочленов  и
и 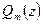 нужно записать подряд все члены этих двух многочленов и затем сделать приведение подобных членов.
нужно записать подряд все члены этих двух многочленов и затем сделать приведение подобных членов.
Для нахождения произведения многочленов  и
и 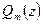 нужно каждый одночлен многочлена
нужно каждый одночлен многочлена  умножить на каждый одночлен многочлена
умножить на каждый одночлен многочлена 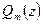 , сложить полученные произведения и привести подобные члены.
, сложить полученные произведения и привести подобные члены.
Основные законы сложения и умножения многочленов.
1.  (коммутативность сложения).
(коммутативность сложения).
2.  (ассоциативность сложения).
(ассоциативность сложения).
3.  (коммутативность умножения).
(коммутативность умножения).
4.  (ассоциативность умножения).
(ассоциативность умножения).
5.  (дистрибутивность сложения относительно умножения).
(дистрибутивность сложения относительно умножения).
Вычесть из  многочлен
многочлен 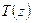 ‑ это значит найти такой многочлен
‑ это значит найти такой многочлен  , что
, что  . Многочлен
. Многочлен  называется разностью многочленов
называется разностью многочленов  и
и 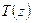 .
.
Два многочлена  и
и  считаются тождественно равными тогда и только тогда, когда равны их степени и равны коэффициенты при одинаковых степенях z. Равенство многочленов записывается так:
считаются тождественно равными тогда и только тогда, когда равны их степени и равны коэффициенты при одинаковых степенях z. Равенство многочленов записывается так:  .
.
В частности, запись  будет означать, что многочлен
будет означать, что многочлен  тождественно равен нулю, т.е. все его коэффициенты равны нулю. Отметим, что если произведение многочленов равно нулю, то хотя бы один из этих многочленов тождественно равен нулю.
тождественно равен нулю, т.е. все его коэффициенты равны нулю. Отметим, что если произведение многочленов равно нулю, то хотя бы один из этих многочленов тождественно равен нулю.
На определении равенства многочленов основан метод неопределенных коэффициентов разложения многочлена на множители. Разберем его на примере.
|
|
|
Пример. Разложить многочлен  на множители, среди которых один многочлен первой степени, а второй ‑ многочлен второй степени.
на множители, среди которых один многочлен первой степени, а второй ‑ многочлен второй степени.
Решение. Так как у многочлена  коэффициент при старшей степени равен единице, то будем искать многочлены
коэффициент при старшей степени равен единице, то будем искать многочлены  и
и  так же со старшими степенями равными единице. Справедливо равенство
так же со старшими степенями равными единице. Справедливо равенство
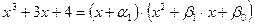 . (*)
. (*)
Перемножив многочлены в правой части равенства (*) и приведя подобные получим:
 . (**)
. (**)
Приравнивая коэффициенты при одинаковых степенях у многочленов, находящихся справа и слева в равенстве (**), получим:
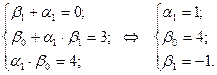
Искомое разложение будет
 .
.
Разделить нацело многочлен  на многочлен
на многочлен  , ‑ это значит найти многочлен
, ‑ это значит найти многочлен  такой, что
такой, что  . Если такой многочлен
. Если такой многочлен  существует, то говорят, что
существует, то говорят, что 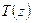 является делителем многочлена
является делителем многочлена  , а многочлен
, а многочлен  называется частным от деления многочлена
называется частным от деления многочлена  на многочлен
на многочлен 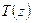 .
.
Не любой многочлен  делится нацело на многочлен
делится нацело на многочлен 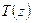 . Например,
. Например, 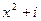 не делится нацело на
не делится нацело на  .
.
Деление с остатком. Разделить с остатком многочлен  на
на  , ‑ это значит найти два многочлена
, ‑ это значит найти два многочлена  и
и  такие, что
такие, что
 (2)
(2)
причем либо степень многочлена  строго меньше степени многочлена
строго меньше степени многочлена 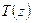 , либо
, либо  есть нуль.
есть нуль.
В случае, когда выполнено равенство (2), говорят, что  делится на
делится на 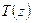 с остатком
с остатком  и частным
и частным  ; если
; если  , то говорят, что
, то говорят, что  делится на
делится на 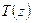 с остатком нуль или делится нацело на
с остатком нуль или делится нацело на 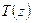 .
.
Пример. Разделить  на
на 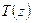 , если
, если  ,
,  .
.
Решение. Делим  на
на 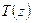 уголком.
уголком.
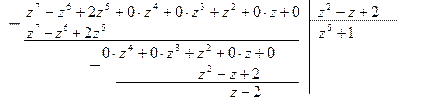
Получили:  , где
, где  и
и  .
.
Для определения коэффициентов многочленов  и
и  существуют и другие способов. Наиболее распространенный из них уже рассмотренный ранее метод неопределенных коэффициентов.
существуют и другие способов. Наиболее распространенный из них уже рассмотренный ранее метод неопределенных коэффициентов.
Пример. Разделить  на
на 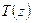 , если
, если 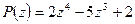 ,
,  .
.
Решение. Так как  , то пологая
, то пологая
 ,
,  ,
,
получим
 .
.
Раскрыв скобки и приведя подобные в правой части этого равенства, имеем
 .
.
Приравнивая коэффициенты при одинаковых степенях у многочленов, находящихся справа и слева, получим:

Откуда находим  ,
,  .
.
|
|
|
Теорема Безу. Корни многочлена и их кратность. Основная теорема алгебры.
Теорема (Безу) Остаток от деления многочлена  на двучлен
на двучлен  равен значению многочлена
равен значению многочлена  при
при  , т.е.
, т.е.  .
.
Доказательство. Подставив в равенство  вместо z значение a, получим
вместо z значение a, получим  , т.е.
, т.е.  . ÿ
. ÿ
Следствие. Многочлен  делится нацело на двучлен
делится нацело на двучлен  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Доказательство.
Необходимость. Пусть  делится нацело на
делится нацело на  . Это означает, что остаток
. Это означает, что остаток  . По теореме Безу
. По теореме Безу  .
.
Достаточность. Пусть  , тогда по теореме Безу
, тогда по теореме Безу  , следовательно,
, следовательно,  , т.е.
, т.е.  делится нацело на двучлен
делится нацело на двучлен  . ÿ
. ÿ
Определение. Комплексное число a называется корнем алгебраического многочлена  , если
, если  .
.
Утверждение 1. Если комплексное число a является корнем многочлена ненулевой степени 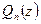 , то для
, то для 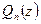 справедливо представление
справедливо представление
 (3)
(3)
в котором  ‑ алгебраический многочлен степени
‑ алгебраический многочлен степени 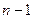 , причем коэффициент при
, причем коэффициент при  у многочлена
у многочлена  совпадает с коэффициентом при
совпадает с коэффициентом при  у многочлена
у многочлена 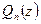 .
.
Доказательство. Так как a ‑ корень многочлена 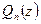 , то
, то  , т.е.
, т.е.  . Вычислим разность
. Вычислим разность  :
:
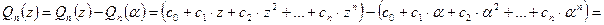
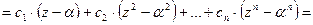
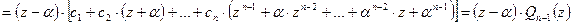
Итак,
 ,
,
где
 .
.
Многочлен  имеет степень
имеет степень 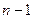 и коэффициент при
и коэффициент при  равен
равен  .ÿ
.ÿ
Возникает вопрос: всякий ли многочлен имеет корень? Ответ на этот вопрос дает
основная теорема алгебры, которую примем без доказательства.
|
|
|


