Определение коэффицентов сопротивление по длине в трубопроводе.

Цель работы:

 

I. Определить опытным путем коэффициенты Дарси λ в трубопроводе при различных скоростях движения воды. 2.Сравнить λ, полученный из опыта, с вычисленными по

Формулам.

 

I. Теоретические сведения.

 

Потери напора по длине h_l при движении вязкой жидкости в напорном трубопроводе определяются по формуле Дарси-Вейсбаха:

 

где λ - коэффициент сопротивления трения по длине –

коэффициент Дарси.

l- длина трубопровода, м;

d - диаметр трубы, м;

ω - средняя скорость, м/c.

Коэффициент Дарси λ является безразмерной переменной величиной, зависящей от ряда характеристик - от диаметра и шеро­ховатости трубы, вязкости и скорости жидкости и др..

В общем виде можно написать λ = f (Re, Δ).

Влияние этих характеристик на величину λ проявляется по разному при различных режимах движения в трубе. В одном диа­пазоне изменения чисел Рейнольдса Re, характеризующих режим движения, на величину λ влияет в большей степени скорости,

в другом диапазоне преобладающее влияние оказывают геометрические характеристики – диаметр шероховатость трубы (высоте выступов шероховатости Δ).

В связи с этим различаются четыре области сопротивления, в которых изменение λ имеет свою закономерность.

Первая область - область ламинарного потока, ограничен зна­чениями Re < 2320, в которой λ зависит от Re и не зависит от величины выступов шероховатости Δ. При ламинарном; режиме λ определяется по формуле Пуазейля:

/1/

Все остальные области сопротивления, находятся в зоне тур­булентного режима с различной степенью турбулентности.

Вторая область – гидравлически гладкие трубы. Поток в тру­бе при этом турбулентный, но у стенок трубы сохраняется слой жидкости δ пределах которого движение остается ламинарным. Трубы считаются гидравлически гладкими, если толщина ламинарного слоя больше высоты выступов шероховатости δ>>Δ. В этом случае ламинарный слой покрывает неровности стенок трубы и пос­ледние не оказывают тормозящего влияния на основное турбулентное ядро потока.

Для гидравлически гладких труб, т.е. при условии δ>>Δ, коэффициент может быть определен по формуле Колбрука:

/2/

которая применима в широком диапазоне чисел Re:

2320< Re <3*10⁶

При числах Re < 10⁵ коэффициент λ для гладких труб можно определить по более простой зависимости, предложенной Блазиусом:

 

/3/

Третья область - переходная от области гидравлически гладких труб к квадратичной области. В этой области толщина, ламинарного слоя равна или меньше выступов шероховатости, которые в этом случае выступают как препятствие у стенок, увеличивая турбулентность, а следовательно, и сопротивление в потоке.

В переходной области коэффициент сопротивления определяется по формуле Френкеля:

 

/4/

Четвертая область - область гидравлически шероховатых труб сопротивления. При стенного ламинарного слоя в этой области нет. Основное влияние на сопротивление потоку оказывает шероховатость стенок трубы. Чем больше выступы шероховатости тем большую турбулентность они вызывают, тем больше будут затраты энергии в потоке на преодоление сопротивлений. В квадратичной области сопротивления коэффициент не зависит от скорости. Коэффициент λ определяется по формуле Никурадзе:

 

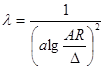/5/

где а, А - величины, зависящие от вида шероховатости

численные значения которых получены только для

разнозернистой шероховатости (а = 2, А = 14,8)

R - гидравлический радиус трубы.

 

 

2. Порядок выполнения работы.

 

Для горизонтального прямолинейного участка трубы постоянного сечения из уравнения Бернулли:

/6/

потери напора по длине будут равны:

/7/

 

Так как для горизонтальной трубы Z₁ = Z₂, то ω₁ = ω₂ если постоян­но сечения.

 

Следовательно, после установления постоянного расхода в трубе надо измерить высоты в пьезометрах 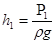и

присоединенных к трубопроводу на расстоянии l один от другого, т.к. разность показаний пьезометров:

то отсюда определяет

Полученное опытное значение λ надо сравнить с расчетным по формуле /1-5/. Для этого следует определить число Rе, а выступы

Шероховатости трубок Δ и выяснить область сопротивления, для которой вычислить λпо соответствующей формуле /1-5/

Так как непосредственное измерение выступов шероховатости в трубе затруднительно, можно воспользоваться справочной таблицей. Например, для металлических труб Δ=0,5—1мм.

Изменяя количество воды в трубе вычислить коэффициент сопротивления λ для различных областей.

 

3. Журнал работы.

Материал трубы..............................; внутренний диаметр d=; площадь сечения м²; высота шероховатости Δ=................мм; расстояние между пьезометрами l=………...м; показание h₁=…………….см; h₂=…………….см.

Потери напора по длине h_l=…………….м. Число Рейнольдса Re = Режим движения………….

 

 

4. Контрольные вопросы.

 

1. От чего зависит изменение коэффициента Дарси λ?

2. Назовите области зависимости λ и сколько их.

3. Что такое гидравлическая, гладкая и гидравлическая

4. шероховатость трубы?

5. Как производится выбор формулы от /I/ - /5/?

 

 

ЛАБОРАТОРНАЯ РАБОТА №4

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: