 |
Тема 3. Расчет дебита многоствольной скважины.
|
|
|
|
Одной из первых и наиболее упоминаемой в литературных источниках зависимостей, описывающих приток к многоствольной горизонтальной скважине, с равномерном веерным расположением в центре круговой залежи, является уравнение Борисова Ю.П., Пилатовского В.П., Табакова В.П.:
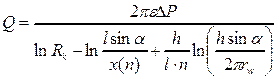, (3.1)
где, п — число стволов, а — угол наклона ствола от вертикали, l — длина отдельного ствола, функция х (п)равна 4; 2; 1.86; 1.78 при числе горизонтальных стволов 1; 2; 3 и 4.
Григулецкий В.Г., Никитин Б.А. анализировали влияние различных факторов на дебит многоствольной горизонтальной одноярусной скважины при помощи несколько измененной формулы (2.2), учитывающей анизотропность пласта:
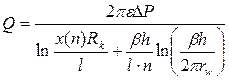, (3.2)
где b = yjkv jkh — параметр анизотропии проницаемости пласта.
Для одноярусной многоствольной горизонтальной скважины известно также уравнение:
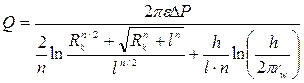. (3.3)
Если принять n =2, то получим формулу Джоши, в которой вместо малой полуоси эллипса используется радиус контура питания, а для описания течения к точечному стоку уравнение Борисова Ю.П.
Формула Меркулова В.П. используется для расчета притока жидкости к кусту скважин с горизонтальными забоями:
, (3.4)
где d – относительное смещение горизонтального ствола от среднего положения в пласте, значения параметров а, b, с,l определяются из формул:
, 
, 
, 
.
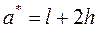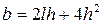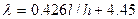В работах авторами рассматривался приток нефти к горизонтальной нефтяной скважине, не полностью вскрывшей сектор. Под сектором понимается часть круговой области дренирования. Для получения определенной закономерности между производительностью горизонтальных скважин и относительным вскрытием сектора авторами путем моделирования изучено влияние: - длины горизонтального ствола L г, т.е. полноты вскрытия сектора на производительность горизонтальных нефтяных скважин; - величины радиуса контура сектора Rк.сек; - числа горизонтальных скважин «n» на изучаемые закономерности и на интенсивность их изменения во времени; - проницаемости пластов; - степени загрязнения призабойной зоны, т.е. величины скин-эффекта; - величины депрессии на пласт на изучаемые зависимости при вскрытии горизонтальным стволом сектора кругового пласта. Такая работа была выполнена на моделях фрагментов нефтяной залежи секторной формы при углах сектора α =450, 300 и 22,50 (рис. 2.1), его радиусах Rк.сек =3000 м и Rк.сек =6000 м, проницаемостях фрагмента k =10, 50, и 250 мД и длинах горизонтального ствола L г равных L г =Rк.сек - Rвход (полное вскрытие сектора); =0,734; =0,467; =0,267.
|
|
|
Решение. Дано:
| Наименование параметра | Условное обозначение | Единицы измерения (СИ) | Значение |
| Длина горизонтального участка | l | м | |
| Проницаемость по горизонтали, м2 | kh | м2 | 147·10-15 |
| Проницаемость по вертикали, м2 | kv | м2 | 36·10-15 |
| Вязкость нефти | μн | Па·с | 0,00098 |
| Пластовое давление | Рпл | Па | 23,1·106 |
| Забойное давление | Рзаб | Па | 16·106 |
| Радиус горизонтального участка скважины | rc | м | 0,1 |
| Радиус контура питания | Rk | м | |
| Угол наклона ствола от вертикали | α | град | |
| Гидропроводность | ε | (м2·м)/(Па·с) | 2,93·10-10 |
| Параметр анизотропии проницаемости пласта | β | 0,244 |
Задача решается следующим порядком:
1. Расчитываем приток жидкости к многоствольной горизонтальной скважине по уравнению Борисова Ю.П., Пилатовского В.П., Табакова В.П.:
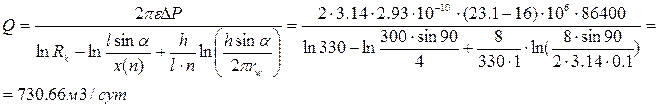2. Расчитываем приток жидкости к многоствольной горизонтальной скважине по уравнению Григулецкого В.Г., Никитина Б.А.:
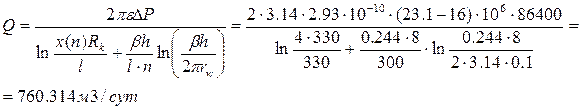
3. Расчитываем приток жидкости по формуле для одноярусной многоствольной горизонтальной скважине:
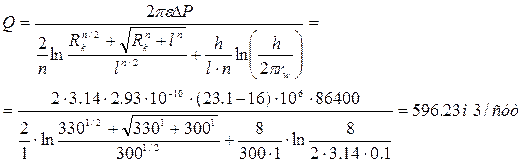
4. Расчитываем приток жидкости к многоствольной горизонтальной скважине по формуле Меркулова В.П.:
|
|
|
| Борисов(90) | Григулецкий | Одноярусная | Меркулова | n |
| 730,6631434 | 760,3145974 | 596,2384087 | 0,07495808 | |
| 1376,646307 | 1429,151989 | 1150,221259 | 0,066873082 | |
| 1533,007256 | 1575,991815 | 1665,044818 | 0,06008589 | |
| 1643,423801 | 1680,271004 | 2143,610059 | 0,054456752 |
Полученные результаты:
Выводы: 1) Методика Борисова. Исходя из данной методики при α=900, бурение многоствольных ГС с равномерным веерным расположением приводит к значительному увеличению дебита скважины. При этом резкое увеличение дебита наблюдается при бурении двух боковых стволов.
|
|
|
