 |
Ширина интерференционной полосы
|
|
|
|
Рассмотрим теперь график распределения интенсивности I (d), который согласно (1) является гармонической функцией. На рис.3 представлена часть графика для d > 0.
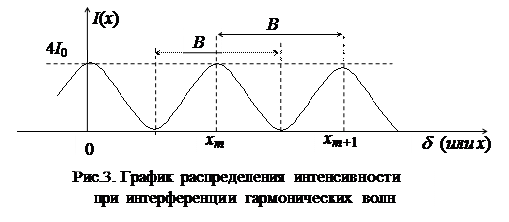
Очевидно, что данный график отражает интерференционную картину, возникающую на экране. Значение d = 0 соответствует центру интерференционной картины; xm и xm+ 1 – два соседних максимума с номерами m и m +1 соответственно. Геометрические места точек в пространстве, куда приходят волны от источников S 1 S 2 (рис.2) с одинаковыми δ (одинаковыми разностями хода D), образуют гиперболоиды вращения с осью S 1 S 2. Поскольку плоскость экрана параллельна S 1 S 2 , а D >> 2 l, сечения гиперболических поверхностей с плоскостью экрана образуют чередующиеся светлые и темные полосы. Расстояние B между парой соседних максимумов (или минимумов) получило название ширины интерференционной полосы.
Величину B можно найти из простых геометрических соотношений, используя схему рис.2. По теореме Пифагора:
 |
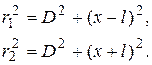Вычтем почленно, разложив разность квадратов в левой части:
(5)
Здесь r 2 – r1 = D, и, поскольку D >> 2 l, можно считать, что r 1 + r 2 @ 2 D. Из (5) найдём координату x произвольной точки на экране
(5)
а для координат двух соседних максимумов (или минимумов) 
и 
. Тогда ширина интерференционной полосы
(6)
Часть II. Экспериментальная часть
Методика эксперимента
Кольца Ньютона являются частным случаем интерференционной картины, осуществляемой методом деления амплитуды. Cвет, отражаясь и преломляясь на каких-либо поверхностях, делится на отдельные потоки, способные к интерференции. Такая интерференция может наблюдаться и в обыденной жизни. Например, радужные переливы тонких пленок нефти на воде, разноцветные мыльные пузыри.
|
|
|
Устройство для получения колец Ньютона состоит из плоскопараллельной стеклянной пластины и плосковыпуклой тонкой линзы, находящейся в оптическом контакте с пластиной. Линза может быть закреплена на пластине (рис.4) или находиться под пластиной. Между линзой и пластиной образуется клинообразный воздушный слой, постепенно утолщающийся к краям линзы. Если на линзу с пластиной сверху направить свет, то вследствие деления световых волн в результате отражения и преломления будет происходить интерференция.
Рассмотрим детально схему возникновения интерференционной картины. На рис 5 изображена линза Л, лежащая на пластинке П. От одной из точек удалённого источника света S идут два когерентных луча 1 и 2. Луч 1 преломляется на нижней поверхности линзы, проходя из стекла в воздух, затем отражается от верхней поверхности пластинки и ещё раз преломляется (луч 
). Луч 2, отражаясь от линзы (луч 
), пересекается с лучом 1 на нижней поверхности линзы на высоте h от поверхности стеклянной пластинки. Таким образом два луча интерферируют на нижней поверхности линзы.
Результат интерференции данной пары лучей, как и всегда, определяется разностью хода. Можно использовать стандартную формулу для разности хода 
двух волн, выведенную при исследовании интерференции методом деления амплитуды:
. (7)
Здесь h – толщина клинообразного воздушного слоя, n - показатель преломления вещества клина, ψ – угол преломления светового луча, λ – длина волны света.
Падение света можно считать нормальным (
), показатель преломления воздуха 
, поэтому формула для разности хода упрощается и принимает вид
. (8)
Таким образом, разность хода волн, интерферирующих на нижней поверхности линзы, зависит только от толщины воздушного клина.
|
|
|
Геометрическим местом точек на поверхности воздушного клина (на нижней поверхности линзы), куда волны приходят с одинаковой разностью хода, будут концентрические кольца (кольца Ньютона) с центрами, лежащими на оси линзы. При наблюдении картины в монохроматическом свете кольца Ньютона имеют вид чередующихся тёмных и светлых колец; в белом свете кольца окрашены.
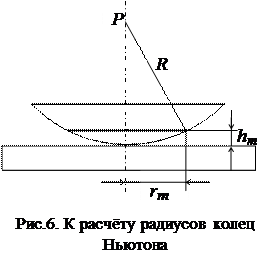На рис.6 выделено одно из колец Ньютона, имеющее порядковый номер m (считая от центра) и радиус rm. Здесь Р - центр кривизны линзы, R - радиус её кривизны.
Согласно теореме Пифагора
,
где hm – толщина воздушного клина. В право й части раскрываем скобки и пренебрегаем малым слагаемым 
. Тогда
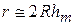. (9)
Выразив 
из (9), получаем вместо (8) выражение для разности хода в виде
. (10)
Теперь можно вывести формулы, определяющие радиусы светлых и тёмных колец Ньютона. Там, где реализуются условия максимума интерференции (D = ml), наблюдаются светлые кольца:
. (11)
Для тёмных колец (
) имеем
, (12)
где m = 1,2,3, ….
Рассмотрим некоторую пару тёмных колец, имеющих порядковые номера m и р. Согласно (12), для этой пары
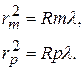
Тогда 
. Эту формулу можно использовать двояко. Например, если измерить радиусы m -гои р -го тёмных колец, то можно найти радиус кривизны линзы:
. (13)
Если же радиус кривизны линзы известен, то можно найти длину волны падающего света:
. (14)
Практическая часть
Оборудование: микроскоп, окулярный микрометр Гюйгенса, объект-микрометр, устройство из плоскопараллельной пластинки и плоско-выпуклой линзы, светофильтры, плоское зеркало.
Установка для получения и наблюдения колец Ньютона изображена на рис.7.
Упражнение 1. Определение увеличения микроскопа
1) На тубус микроскопа надеть окулярный микрометр Гюйгенса с известной ценой деления.
2) На предметный столик микроскопа положить объект-микрометр.
3) Перемещая винт микроскопа и поворачивая направляющее зеркало, получить изображение шкалы объект-микрометра в поле зрения микроскопа (рис.8).
4) Вращением барабана микроскопа совместить центр перекрестия окулярного микрометра с одним из делений объект-микрометра (рис.8). (Следует пользоваться центральной частью поля зрения окуляра, поскольку на краях качество изображения хуже.) Записать показание в виде числа 
. Целая часть (число целых миллиметров) отсчитывается по шкале окулярного микрометра до биштриха. Сотые доли числа отсчитываются по шкале барабана окулярного микрометра.
|
|
|
5) Передвинуть перекрестие на z делений, совместив его с каким-либо другим штрихом шкалы объект-микрометра. Записать второй отсчёт в виде числа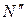 
.
7) Повторить измерения пп.4 и 5 не менее 5 раз. Результаты занести в табл. 1.
Таблица 1
|
|
|
