 |
История интегрального и дифференциального исчисления
|
|
|
|
Введение
Факультативный курс «Применение дифференциального и интегрального исчисления к решению физических и геометрических задач» имеет своей целью изучение курса математического анализа на основе практического освещения материала, на основе использования методов данного раздела математики для решения задач геометрии и физики; а так же реализации этих задач на компьютере (с помощью пакета MATLAB).
В результате можно сказать, что такое объёмное, не конкретное формулирование темы и цели факультативного курса даёт возможным его реализацию в школе. В школьном курсе алгебры и начал анализа курс «Применение дифференциального и интегрального исчисления к решению физических и геометрических задач» направлен на изучение определённого интеграла.
Место темы в школьном курсе математики.
Факультативный курс «Применение интегрального исчисления к решению физических и геометрических задач» углубляет материал курса алгебры и начал анализа в одиннадцатом классе и раскрывает возможности для практического закрепления материала по темам, входящим в школьный курс математики. Это темы «Производная функции», «Определённый интеграл» в алгебре, и некоторые темы в геометрии и физике. В результате данный факультативный курс реализует межпредметную связь алгебры и математического анализа с геометрией, информатикой и физикой.
Развитию у учащихся правильных представлений о характере отражения алгеброй основных элементов в геометрии и физике, роли математического моделирования в научном познании способствует знакомство их с решением и визуализацией различных математических задач на компьютере. Изложение факультативного курса базируется на основных возможностях версии 6.1 пакета математических и инженерных вычислений MATLAB, ставшего в настоящее время стандартным средством поддержки изучения высшей математики, численного анализа и других учебных курсов во многих университетах. Учащимся излагаются основные возможности численных и символьных вычислений, программирования и визуализации результатов, предоставляемые ядром системы MATLAB и его пакета расширения Symbolic Math Toolbox.
|
|
|
Основные понятия факультативного курса: определённый интеграл, длина кривой, площадь, поверхность вращения, цилиндрическая поверхность, объём тела и др.
Цели факультативного курса.
1. Обучающие: провести практическое закрепление по теме «Определённый интеграл», познакомить учащихся с пакетом математических и инженерных вычислений MATLAB 6.1, проиллюстрировать реализацию межпредметной связи математического анализа с геометрией, информатикой и физикой.
2. Воспитывающие: создание условий для успешного профессионального самоопределения учащихся посредством решения трудных задач с использованием компьютера, воспитание мировоззрения и ряда личностных качеств, средствами углубленного изучения математики.
3. Развивающие: расширение кругозора учащихся, развитие математического мышления, формирование активного познавательного интереса к предмету, развитие профессиональных интересов учащихся, развитие навыков самостоятельной и исследовательской деятельности, развитие рефлексии учащихся (осознание своих склонностей и способностей, необходимыми для будущей профессиональной деятельности).
История интегрального и дифференциального исчисления
История понятия интеграла тесно связана с задачами нахождения квадратур. Задачами о квадратуре той или иной плоской фигуры математики Древней Греции и Рима называли задачи, которые мы сейчас относим к задачам на вычисление площадей. Латинское слово quadratura переводится как «придание квадратной формы». Необходимость в специальном термине объясняется тем, что в античное время (и позднее, вплоть до XVIII столетия) еще не были достаточно развиты привычные для нас представления о действительных числах. Математики оперировали с их геометрическими аналогами или скалярными величинами, которые нельзя перемножать. Поэтому и задачи на нахождение площадей приходилось формулировать, например, так: «Построить квадрат, равновеликий данному кругу». (Эта классическая задача «о квадратуре круга» не может, как известно, быть решена с помощью циркуля и линейки.)
|
|
|
Многие значительные достижения математиков Древней Греции в решении задач на нахождение квадратур (т. е. вычисление площадей) плоских фигур, а также кубатур (вычисление объемов) тел связаны с применением метода исчерпывания, предложенным Евдоксом Книдским (ок. 408 — ок. 355 до н.э.). Метод Евдокса был усовершенствован Архимедом (ок. 287 – 212 до н.э.). С этой модификацией вы знакомы: вывод формулы площади круга, предложенный в курсе геометрии, основан на идеях Архимеда
Его остроумные и глубокие идеи, связанные с вычислением площадей и объёмов тел, решением задач механики, по существу, предвосхищают открытие математического анализа и интегрального исчисления, сделанное почти 2000 лет спустя. Добавим, что практически и первые теоремы о пределах были доказаны им.
Кроме этого Архимед дал оценку числа «пи» (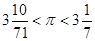
), нашел объемы шара и эллипсоида, площадь сегмента параболы и т. д. Сам Архимед высоко ценил эти результаты: согласно его желанию на могиле Архимеда высечен шар, вписанный в цилиндр (Архимед показал, что объем такого шара равен 2/3 объема цилиндра).
Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Активно применялся и другой метод — метод неделимых, который также зародился в Древней Греции (он связан в первую очередь с воззрениями Демокрита). Например, криволинейную трапецию они представляли себе составленной из вертикальных отрезков длиной f (х), которым, тем не менее, приписывали площадь, равную бесконечно малой величине f(x)dx. В соответствии с таким пониманием искомая площадь считалась равной сумме 
бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме – нули, но нули особого рода, которые, сложенные в бесконечном числе, дают вполне определенную положительную сумму.
|
|
|
На такой кажущейся теперь, по меньшей мере, сомнительной основе И. Кеплер (1571—1630) в своих сочинениях «Новая астрономия» (1609 г.) и «Стереометрия винных бочек» (1615 г.) правильно вычислил ряд площадей (например, площадь фигуры, ограниченной эллипсом) и объемов (тело разрезалось на бесконечно тонкие пластинки). Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598—1647) и Э. Торричелли (1608—1647). Сохраняет свое значение и в наше время сформулированный Б. Кавальери принцип для площадей плоских фигур: Пусть прямые некоторого пучка параллельных пересекают фигуры Ф1 и Ф2 по отрезкам равной длины. Тогда площади фигур Ф1 и Ф2 равны.
Аналогичный принцип действует в стереометрии и оказывается полезным при нахождении объемов. Простейшие следствия принципа Кавальери вы можете вывести сами. Докажите, например, что прямой и наклонный цилиндры с общим основанием и высотой имеют равные объемы.
В XVII в. были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П. Ферма уже в 1629 г. решил задачу квадратуры любой кривой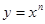 
, где п — целое (т. е. по существу вывел формулу 
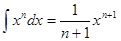, и на этой основе решил ряд задач на нахождение центров тяжести.
Однако при всей значимости результатов, полученных многими чрезвычайно изобретательными математиками XVII столетия, исчисления еще не было. Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно общий алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный вам под названием формулы Ньютона — Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.
|
|
|
Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa). Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integro, которое переводится, как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования «восстанавливает» функцию, дифференцированием которой получена подынтегральная функция.) Возможно, происхождение термина интеграл иное: слово integer означает целый.
В ходе переписки И. Бернулли и Г. Лейбниц согласились с предложением Я. Бернулли. Тогда же, в 1696 г., появилось и название новой ветви математики — интегральное исчисление (calculus integralis), которое ввел И. Бернулли.
Другие известные вам термины, относящиеся к интегральному исчислению, появились заметно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее «примитивная функция», которое ввел Лагранж (1797 г.). Латинское слово primitivus переводится как «начальный»: 
— начальная (или первоначальная, или первообразная) для f(x), которая получается из F(х) дифференцированием.
В современной литературе множество всех первообразных для функции f(х) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную. А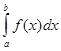 
называют определенным интегралом (обозначение ввел К. Фурье (1768—1830), но пределы интегрирования указывал уже Эйлер).
Методы математического анализа активно развивались в следующем столетии. В развитии интегрального исчисления приняли участие русские математики М. В. Остроградский (1801—1862), В. Я. Буняковский (1804-1889), П. Л. Чебышев (1821—1894).
Строгое изложение теории интеграла появилось только в прошлом веке. Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков немецкого ученого Б. Римана (1826—1866, см. рис. 4.), французского математика Г. Дарбу (1842— 1917).
Дифференциал в физике
Мы ввели понятие дифференциала с помощью равенства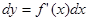 
. Для вычисления дифференциала надо найти производную. Однако, помня о том, что дифференциал — это главная часть приращения функции, линейно зависящая от приращений аргумента, мы из физических соображений получим равенства вида dy = kdx и сделаем вывод о том, что k — это производная у по х.
1. Работа. Найдем работу, которую совершает заданная сила F при перемещении по отрезку оси х. Если сила F постоянна, то работа А равна произведению F на длину пути. Если сила меняется, то ее можно рассматривать как функцию от х: F = F (x). Приращение работы А на отрезке [х, x + dx ] нельзя точно вычислить как произведение F (x) dx, так как сила меняется, на этом отрезке. Однако при маленьких dx можно считать, что сила меняется незначительно и произведение представляет главную часть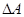 
, т. е. является дифференциалом работы (dA = = F (x) dx). Таким образом, силу можно считать призводной работы по перемещению.
|
|
|
2. Заряд. Пусть q — заряд, переносимый электрическим током через поперечное сечение проводника за время t. Если сила тока / постоянна, то за время dt ток перенесет заряд, равный Idt. При силе тока, изменяющейся со временем по закону / = /(/), произведение I (t) dt дает главную часть приращения заряда на маленьком отрезке времени [/, t +- dt ], т.е.- является дифференциалом заряда: dq = I { t) dt. Следовательно, сила тока является производной заряда по времени.
3. Масса тонкого стержня. Пусть имеется неоднородный тонкий стержень. Если ввести координаты так, как показано на рис. 130, то функция т= т(1) — масса куска стержня от точки О до точки /. Неоднородность стержня означает, что его линейная плотность не является постоянной, а зависит от положения точки / по некоторому закону р = р(/). Если на маленьком отрезке стержня [/, / + d/] предположить, что плотность постоянна и равна р(/), то произведение p(/)d/ дает дифференциал массы dm. Значит, линейная плотность — это производная массы по длине.
4. Теплота. Рассмотрим процесс нагревания какого-нибудь вещества и вычислим количество теплоты Q { T), которое необходимо, чтобы нагреть 1 кг вещества от 0 °С до Т. Зависимость Q = Q (T) очень сложна и определяется экспериментально. Если бы теплоемкость с данного вещества не зависела от температуры, то произведение cdT дало бы изменение количества теплоты. Считая на малом отрезке [ T, T + dT ] теплоемкость постоянной, получаем дифференциал количества теплоты dQ = c (T) dT. Поэтому теплоемкость — это производная теплоты по температуре.
5. Снова работа. Рассмотрим работу как функцию времени. Нам известна характеристика работы, определяющая ее скорость по времени, — это мощность. При работе с постоянной мощностью N работа за время dt равна Ndt. Это выражение представляет дифференциал работы, т.е. dA = N (t) dt, и мощность выступает как производная работы по времени.
Все приведенные примеры были построены по одному и тому знакомыми нам из курса физики: работа, перемещение, сила; заряд, время, сила тока; масса, длина, линейная плотность; и т. д. Каждый раз одна из этих величин выступала как коэффициент пропорциональности между дифференциалами двумя других, т. е. каждый раз появлялось соотношение вида dy = k (x) dx. На такое соотношение можно смотреть как на способ определения величины k (x). Тогда k (x) находится (или определяется) как производная у по х. Этот вывод мы и фиксировали в каждом примере. Возможна и обратная постановка вопроса: как найти зависимость у от х из заданного соотношения между их дифференциалами.
3. Приложения определенного интеграла к решению некоторых задач механики и физики
1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y = f (x), a ≤ x ≤ b, и имеет плотность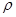 
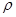= (x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и O y равны
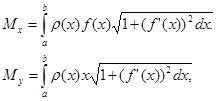
моменты инерции I Х и I у относительно тех же осей Ох и Оу вычисляются по формулам
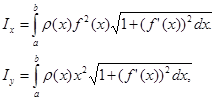
а координаты центра масс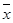 
и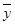 
— по формулам
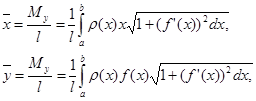
где l — масса дуги, т. е.
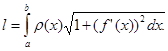
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох
и Оу дуги цепной линии y = chx при 0 ≤ x ≤ 1.
◄ Имеем: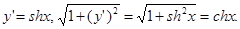 
Следовательно,
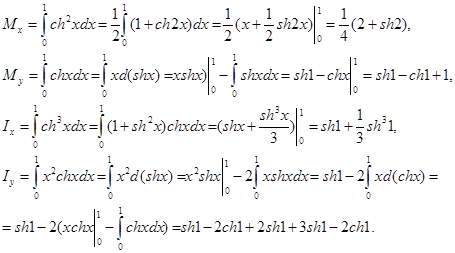
В приложениях часто оказывается полезной следующая
Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.
Пример 2.Найти координаты центра масс полуокружности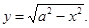 
◄Вследствие симметрии 
. При вращении полуокружности вокруг оси Ох получается сфера, площадь поверхности которой равна 
, а длина полуокружности равна па. По теореме Гульдена имеем 
Отсюда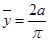 
, т.е. центр масс C имеет координаты C 
.
2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах.
Пример 4. Скорость прямолинейного движения тела выражается формулой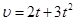 
(м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
◄ Так как путь, пройденный телом со скоростью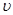 
(t) за отрезок времени [t1,t2], выражается интегралом
то имеем:
►
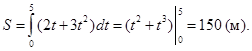4. Дифференциальные уравнения
Многие физические законы имеют вид дифференциальных уравнений, т. е. соотношений между функциями и их производными. Задача интегрирования этих уравнений — важнейшая задача математики. Одни дифференциальные уравнения удается проинтегрировать в явном виде, т.е. записать искомую функцию в виде формул. Для решения других до сих пор не удается найти достаточно удобных формул. В этих случаях можно найти приближенные решения с помощью вычислительных машин. Мы не будем подробно изучать методы интегрирования дифференциальных уравнений, а только рассмотрим несколько примеров.
Примеры
1. Уравнение механического движения. Пусть материальная точка массы т движется под действием силы F по оси х. Обозначим t время ее движения, и — скорость, а — ускорение. Второй закон Ньютона, а = Fm примет вид дифференциального уравнения, если записать ускорение, а как вторую производную: a = x ’’.
Уравнение тх" = F называют уравнением, механического движения, где x = x (t) —неизвестная функция, т и F — известные величины. В зависимости от условий задачи по-разному и записываются различные дифференциальные уравнения.
2. Радиоактивный распад
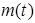— масса распадающего вещества. Количество распадающего вещества 
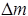пропорционально количеству 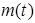и времени, т.е. 
при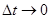 
имеем
.
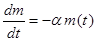Решение дифференциального уравнения-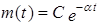 
. Дополнительные условия- 
, тогда задача
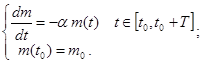
Решение задачи: 
3.Движение системы N материальных точек.
Система уравнений Ньютона
,
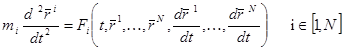-масса,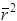 
- радиус вектор i- ой точки, 
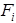- сила воздействующая на i -ую точку.
Частный случай колебания маятника
.
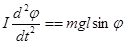При малых колебаниях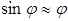 
и тогда уравнение имеет вид:
.
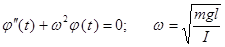4. Прогибание упругого стержня.
Если стержень однороден, то вдоль стержня постоянное касательное натяжение 
. Тогда вертикальная сила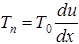 
в точке x, где смещение u(x). Если в каждой точке стержня действует внешняя сила 
то
.
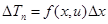Откуда
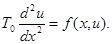
Рассмотрим частный случай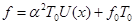 
, тогда получаем уравнение
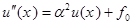
и его решение
.
Дополнительные условия (закрепленные концы) -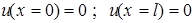 
. Тогда задача
.
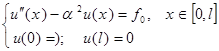Ответ:
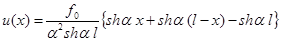
5. Примеры решения задач в matlab
Задача 1. Построить семейство функций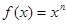 
(
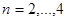) и найти их общие точки, при чём в объекте Figure подписать графики и точки, обозначить оси, подписать заголовок 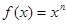и использовать разные цвета для построенных графиков. При решении использовать функцию num2str(x), переводящее число x в строковую величину:
Программа:
x=-2:0.1:2;
title('{\itf(x)=x^{n}}');
xlabel('x');
ylabel('y');
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
hText=text;
set(hText,'FontSize',[18]);
for n=2:4
y=x.^n;
hold on
hPlot=plot(x,y);
set(hPlot,'Color',[1.8/n 0.7 0.5]);
set(hPlot,'LineWidth',2);
if n~=2
for i=1:length(y)
s='';
if y(i)==y1(i)
hold on
plot(x(i),y(i),'ko');
s=['(' num2str(x(i)) ',' num2str(y(i)) ')'];
hText=text(x(i),y(i)+2, s); set(hText,'FontSize',[16]);
end
end
end
y1=y; s2=['n=' num2str(n)];
hText=text(1.5, 1.5^2*n-1, s2); set(hText,'FontSize',[14]);
end
Результат (рис. 12):
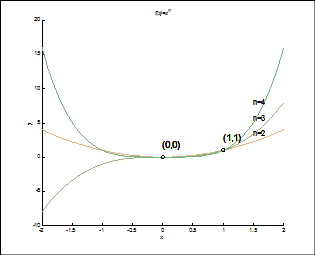
Задача 2. Написать программу-функцию, строящую график функции (funstr) и касательную к нему в точке х0.
Программа:
function kasat(funstr,x0)
f=sym(funstr); y0=subs(f,'x',x0); A=x0-1; B=x0+1; X=[A:(B-A)/100:B]; F=subs(f,'x',X);
Hline=plot(X,F); set(Hline,'LineWidth',2)
syms x
k=diff(f,x,1); K=subs(k,'x',x0); yt=sym('y0+k*(x-x0)');
yt=subs(yt,'k',K); yt=subs(yt,'x0',x0); yt=subs(yt,'y0',y0);
hold on
ezplot(yt,[A B])
plot(x0,y0,'o')
grid on
Результат (рис. 13): >> kasat('x^4',2)
Задача 3. Построить поверхность вращения графика функции заданной явно: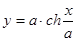 
(где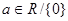 
), вокруг оси Ох.
Результат (рис. 14)
Программа:
x1=0; x2=2; a=1;
u=x1:0.1:x2;
v=0:pi/20:2*pi;
[U,V]=meshgrid(u,v);
F=a*(exp(-U/a)+exp(U/a))/2;
X=U; Y=F.*cos(V); Z=F.*sin(V);
figure; hFigure=gcf;
set(hFigure,'Color',[0.9 0.8 0.8]);
surf(X,Y,Z)
colorbar;
view([-75,20])
hold on
x=0:0.1:x0; y=a*(exp(-x/a)+exp(x/a))/2;
hPlot=plot(x,y); set(hPlot,'LineWidth',5)
Задача 4. Визуализировать поверхность, образованной вращением астроиды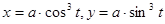 
.
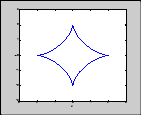
Результат (рис. 15,16)
Программа:
Построение астроиды
a=2;
t=-2*pi:pi/20:2*pi;
X=a*cos(t).^3;
Y=a*sin(t).^3;
w=300;
h=300; figure('Units','Pixels','position',
[100,100,w,h]);
plot(X,Y)
xlabel('x'); ylabel('y');
axis([-3, 3, -3, 3]);
% Поверхность вращения
a=2;
t=-2*pi:pi/20:2*pi;
X=a*cos(t).^3;
v=0:pi/20:2*pi;
[T,V]=meshgrid(t,v);
Y=a*sin(T).^3;
X1=X;
Y1=Y.*cos(V);
Z1=Y.*sin(V);
figure;
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
surf(X1,Y1,Z1)
hAxes=gca;
set(hAxes,'Color',[0.9,0.9,0.9]);
colorbar;
xlabel('x'); ylabel('y'); zlabel('z');
view([-24,40])
hold on
hPlot=plot(X,Y);
set(hPlot,'LineWidth',5)
set(hPlot,'Color',[1 0 1])
Задача 5. Построить в полярных координатах лемнискату Бернулли: 
.
Программа:
a=1;
r=[]; phi=[];
for p=0:pi/60:2*pi
if 2*a^2*cos(2*p)>=0
r=[r sqrt(2*a^2*cos(2*p))];
phi=[phi p];
end
end
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
hP=polar(phi,r);
set(hP,'LineWidth',2);
Результат (рис. 17):
Задача 6. Используя численные и символьные вычисления в MATLAB найти: а) определённый интеграл; б) двойной интеграл; в) поверхностный интеграл (1-го рода).
а) Классической задачей численного анализа является задача о вычислении определённых интегралов. Из всех методов вычисления определённых интегралов самым простым, но в то же время довольно успешно применяемым является метод трапеции. В MATLAB для этого метода предусмотрена функция: trapz(x,y) (команда edit trapz позволяет вывести текст этой функции). Одномерный массив х (вектор) содержит дискретные значения аргументов подынтегральной функции. Значения подынтегральной функции в этих точках сосредоточены в одномерном массиве y. Чаще всего для интегрирования выбирают равномерную сетку, то есть значения элементов массива х отстоят друг от друга на одну и ту же величину – шаг интегрирования. Точность вычисления интеграла зависит от величины шага интегрирования: чем меньше этот шаг, тем больше точность.
Задача 7. Вычислить интеграл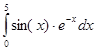 
методом трапеции с различными шагами интегрирования (для наблюдения 14 десятичных цифр после запятой нужно предварительно ввести и исполнить команду format long).
Программа: Результат:
function t=trap(dx)
x=0:dx:5;
y=sin(x).*exp(-x);
t=trapz(x,y); >> format long
>> trap(1)
ans = 0.42255394026468
>> trap(0.1)
ans = 0.50144886299125
>> trap(0.01)
ans = 0.50226667654901
>> trap(0.001)
ans = 0.50227485744814
Метод трапеций является очень универсальным методом и хорошо подходит интегрирования не слишком гладких функций. Если же функция под знаком интеграла является гладкой (существуют и непрерывны несколько первых производных), то лучше применять методы интегрирования более высоких порядков точности. При одном и том же шаге интегрирования методы более высоких порядков точности достигают более точных результатов.
В системе МАТLАВ методы интегрирования более высоких порядков точноcти реализуются функциями quad (метод Симпсона) и quad8 (метод Ньютона-Котеса 8-го порядка точности). Оба этих метода являются к тому же адаптивными. Последнее означает, что пользователю нет необходимости контролировать достигнутую точность результата путем сравнения последовательных значении, соответствующих разным шагам интегрирования. Все это указанные данные функции выполняют самостоятельно.
У функции quad8 более высокий порядок точности по сравнению с функцией quad, что очень хорошо для гладких функций, так как обеспечивается более высокая точность результата при большем шаге интегрирования (меньшем объеме отчислений). Однако функция quad может иметь не меньшее, а даже большее быстродействие для не слишком гладких функций (разрывны или велики по абсолютной величине вторая или третья производные). В любом случае обе эти функции по умолчанию обеспечивают одинаковую относительную точность результата, равную 0.001.
Как и многие другие функции системы МАТLАВ, функции quad и quad8 могут принимать различное количество параметров. Минимальный формат вызова этих функций включает в себя три параметра: имя подынтегральной функции, нижний предел интегрирования и верхний предел интегрирования. Если применяется четвертый параметр, то он является требуемой относительной точностью результата вычислений. Кстати, если обе эти адаптивные функции не могут обеспечить получение необходимой точности (расходящийся или близкий к этому интеграл), то они возвращают символическую бесконечность Inf.
Для вычисления определённых интегралов символьными методами можно использовать два варианта решения: напрямую или по этапам (с подстановкой символьных чисел).
Задача 8. Вычислить определённый интеграл 
.
Программа: Результат:
a1=sym('0'); b1=sym('2');
syms w t a b
w=t^2;
% 1 способ: работа с подстановкой символьных чисел
symbol=int(w,'t',a,b)
symbol2a=subs(symbol,[a,b],[a1,b1])
digits(20);
number=vpa(symbol2a)
% 2 способ: работа с символьными числами
symbol2b=int(w,'t',a1,b1) symbol =
1/3*b^3-1/3*a^3
symbol2a =
8/3
number =
2.6666666666666666667
symbol2b =
8/3
Задача 9. Вычислить площадь поверхности, полученной вращением астроиды вокруг оси Ox: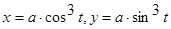 
. (поверхность визуализирована в задаче 2).
Программа: Результат:
t1=sym('0'); t2=sym('pi/2'); a=sym('1');
syms x y t f
x=a*cos(t)^3; y=a*sin(t)^3;
f=y.*sqrt(diff(x)^2+diff(y)^2);
symbol=simplify(int(4*pi*f,'t',t1,t2))
digits(10);
number=vpa(symbol) symbol =
12/5*pi
number =
7.539822370
б) Двойные интегралы сводятся к вычислению повторных определённых интегралов, один из которых является внутренним, а другой внешним. Внутренний интеграл является подынтегральной функцией для внешнего интеграла. Можно было бы для численных вычислений написать некоторую цепочку вычислений, в которой многократные вычисления подынтегральной функции сводились бы к многократным вызовам функции quad. Однако нет необходимости делать это самостоятельно, так как в системе MATLAB для этого имеется специальная функция dblquad.
Задача 8. Вычислить интеграл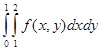 
, где 
.
Программа:
Результат:
function z=fof(x,y)
z=x.*sin(y)+y.*sin(x); >> format long
>> dblquad('fof',0,1,1,2)
ans =
1.16777110966887
Задача 9. С помощью символьных вычислений получить следующие интегралы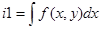 
, 
, 
, 
, 
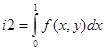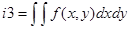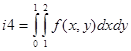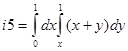, где 
.
Программа:
syms x y
z=sym('x*sin(y)+y*sin(x)');
i1=int(z,'x')
i2=int(z,'x',0,1)
i3=int(int(z,'x'),'y')
i4=int(int(z,'x',1,2),'y',0,1)
digits(14);
number4=vpa(i4)
i5=int(int(x+y,'y',x,1),'x',0,1) i1 =
1/2*x^2*sin(y)-y*cos(x)
i2 =
1/2*sin(y)-y*cos(1)+y
i3 =
-1/2*x^2*cos(y)-1/2*y^2*cos(x)
i4 =
-1/2*cos(2)-cos(1)+3/2
number4 =
1.1677711124054
i5 =
1/2
Так как символьные вычисления не дают погрешности метода вычисления и сами по себе они более точные, то можно увидеть, что функция dblquad даёт точный результат до 7 знака после запятой.
в) Из высшей математики известно, что к определенным и двойным интегралам могут быть сведены многие другие типы интегралов, например поверхностный интеграл 1-го рода. Так как при его нахождении используется дифференцирование под знаком интеграла, то использовать численные вычисления некорректно.
Задача 10. Вычислить поверхностный интеграл 1-го рода: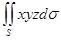 
, где S – часть плоскости 
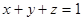, лежащая в первом октанте (по теореме 2).
Программа: Результат:
syms x y z f1 f2
f1=1-x-y;
f2=x*y*z;
fun=subs(f2,z,f1)
d=1+diff(f1,x)^2+diff(f1,y)^2
syms x1 x2 y1 y2
x1=sym('0');
x2=sym('1');
y1=sym('0');
y2=sym('1-x');
intpov1=int(int(fun*sqrt(d),'y',y1,y2),'x',x1,x2)
digits(10);
number=vpa(intpov1) fun =
x*y*(1-x-y)
d =
3
intpov1=
1/120*3^(1/2)
number =
1443375673e-1
Задача 11. Вычислить поверхностный интеграл 1-го рода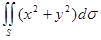 
, где S - сфера 
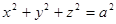(по теореме 3).
Сначала создадим функцию, описывающую поверхность по которой происходит интегрирование:
function [x,y,z]=pov;
syms x y z u v a
x=a*sin(u)*cos(v);
y=a*sin(u)*sin(v);
z=a*cos(u);
Программа:
syms x y z u v a
f=sym('x^2+y^2');
[x0,y0,z0]=pov;
syms E G F W
E=diff(x0,'u')^2+diff(y0,'u')^2+diff(z0,'u')^2;
G=diff(x0,'v')^2+diff(y0,'v')^2+diff(z0,'v')^2;
F=diff(x0,'u')*diff(x0,'v')+diff(y0,'u')*
diff(y0,'v')+diff(z0,'u')*diff(z0,'v');
W=sqrt(E*G-F^2); f2=W*subs(f,[x,y],[x0,y0]);
syms u1 u2 v1 v2
u1=sym('0');
u2=sym('pi/2');
v1=sym('0');
v2=sym('pi/2');
p=sym('8');
intpov=p*int(int(f2,'v',v1,v2),'u',u1,u2)
intpov2=simplify(intpov)
digits(10);
number=vpa(intpov2)
b=sym('1');
int=subs(intpov2,a,b) intpov =
4/3*a^2*pi*(a^4)^(1/2)*4^(1/2)
intpov2 =
8/3*a^4*pi*csgn(a^2)
number =
8.377580412*a^4*csgn(a^2)
int =
8/3*pi
Примечание. Функция сsgn является специфической в MATLAB. Она не может быть введена пользователем и возникает только при оперировании с функцией simplify (упрощение символьных выражений). Например:
>> syms a t
>> t=csgn(a^2)*a^2
??? Undefined function or variable 'csgn'.
>> simplify((a^4)^(1/2))
ans =
csgn(a^2)*a^2
>> simplify((a^8)^(1/4))
ans =
(a^8)^(1/4)
>> simplify((a^9)^(1/3))
ans =
(a^9)^(1/3)
|
|
|
