Система посимвольной синхронизации

Посимвольная синхронизация используется при посимвольном приеме кодовых слов и обеспечивает разделение элементарных сигналов, соответствующих различным позициям кодового слова. Требования к точности посимвольной синхронизации зависят от используемого способа обработки элементарных информационных сигналов в приемнике. При обработке, близкой к оптимальной, а она в нашем случае именно такая, необходимо достаточно точное определение границ этих сигналов. Требования к точности синхронизации возрастают с уменьшением длительности элементарных сигналов.

Рисунок 3. Функциональная схема инерционной системы посимвольной синхронизации

Для выделения сигналов посимвольной синхронизации непосредственно используется последовательность принимаемых информационных символов. На Рисунок 3 показана функциональная схема инерционной системы посимвольной синхронизации. В результате дифференцирования сигнала , образуется последовательность импульсов, временное положение которых соответствует границам между соседними символами «1» и «0». Эта последовательность поступает на временной дискриминатор, который вырабатывает управляющее напряжение, пропорциональное временнóму рассогласованию между входной и опорной последовательностью импульсов. Последняя и используется в качестве сигналов посимвольной (тактовой) синхронизации. Опорная последовательность вырабатывается генератором синхронизирующих сигналов. С помощью управляющего напряжения изменяется частота следования импульсов опорной последовательности, тем самым обеспечивается автоматическая подстройка генератора синхронизирующих сигналов.

Анализ таких систем имеет целью определить флюктуации моментов временных меток относительно положения, соответствующих идеальной ра­боте. В качестве показателя точности можно взять среднеквадратическую ошибку, которая для нормальной работы должна быть много меньше длительности одного символа.

Определение параметров имитационной модели

1) Источник дискретных сообщений:

- дискретные независимые сообщения с заданными вероятностями появления в источнике V(1) = 4;

- количество различных сообщений JU = 32;

- вероятность появления различных значений сообщения A(1...18) = 0.055;

2) Кодирующее устройство:

- двоичный безызбыточный код V(2) = 1;

- количество символов NS = 5;

3) Радиоканал:

- радиоканал, использующий сигнал КИМ-ФМ и приемный тракт с линейным усилением, синхронным детектором и интегратором V(7) = 1, V(9) = 1;

- девиация фазы равна , что соответствует A(172) = 0.577;

- длительность интегрирования, отнесенная к длительности символа A(171) = 0.8, т. е. время интегрирования равно длительности символа;

4) Аддитивные помехи:

- широкополосная шумовая помеха. На входе радиоканала такая помеха представляет собой “белый” шум.

- параметром модели помехи является дисперсия . Таким образом, A(151) = 0.295;

5) Замирание амплитуды сигнала (фединг):

- замирания амплитуды отсутствует V(6) = 1;

6) Временное положение меток системы символьной синхронизации:

- флюктуация временного положения меток отсутствуют (символьная синхронизация идеальная) V(3) = 1;

- номинальное положение метки 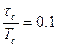, соответственно A(131) = 0.1;

7) Флюктуация фазы опорного напряжения синхронного детектора:

- идеальный синхронный детектор V(4) = 0;

8) Декодирующее устройство:

- однопороговое распознание двоичных символов и декодирование кодовых слов с помощью метрики Хэмминга V(8) = 1;

- порог A(191) = 0;

9) Продолжительность эксперимента:

- продолжительность машинного эксперимента определяется объемом исследуемой выборки сообщений (кодовых слов). Возьмем количество слов равное количеству команд переданных за сеанс связи M = 3000;

10) Дополнительные параметры:

- IX = 7.

Анализ результатов расчета и моделирования

Расчеты, проведенные при выборе базового варианта радиолинии, дали следующие показатели достоверности приема информации:

· вероятность ошибки символа – ;

· вероятность отказа от декодирования – ;

· вероятность ошибки кодового слова – ;

В результате моделирования получены следующие оценки достоверности:

· вероятность ошибки символа – ;

· вероятность отказа от декодирования – ;

· вероятность ошибки кодового слова – ;

При моделировании была взята выборка командных слов, что соответствует длительности сеанса 8 минут.

Заметим, что результаты расчета и моделирования более чем близки по своим значениям, при этом показатели в обоих случаях удовлетворяют ТЗ.

Оценим точность статического эксперимента при моделировании, учитывая количество независимых испытаний в данном эксперименте их 3000.

· вероятность ошибки символа равна ;

· вероятность отказа от декодирования равна ;

· вероятность ошибки кодового слова равна ;

Подведем итог. Все получившиеся различия в результатах расчета и моделирования, являются неизбежными, так как всего в нашей с вами жизни не учтешь.

Литература

1. “Теория и проектирование радиосистем”, Л. В. Березин, В. А. Вейцель. – М.: Сов. радио, 1977.

2. “Основы радиоуправления”, под ред. В. А. Вейцеля и В. Н. Типугина. – М.: Сов. радио, 1973.

3. “Радиотехнические системы передачи информации”, П. И. Пеннин, Л. И. Филиппов. – М.: Радио и связь, 1984.

4. “Автоматизированная модель радиолинии с цифровой передачей информации”, уч. пособие, В. А. Вейцель, С. С. Нужнов. – М.: МАИ, 1985.

5. “Методические указания к курсовому проекту «Радиолинии с цифровой передачей информации»”, авт.-сост. В. А. Вейцель, А. И. Куприянов, М. И. Жодзишский. – М.: МАИ, 1987.

 

[1] см. “Теория и проектирование радиосистем”, Л. В. Березин, В. А. Вейцель. – М.: Сов. радио, 1977. стр. 202

12	Поделиться:

Воспользуйтесь поиском по сайту: