 |
Методы организация таблиц идентификаторов
|
|
|
|
Выделение идентификаторов и других элементов исходной программы происходит на фазе лексического анализа. Для хранения найденных идентификаторов и их характеристик используются специальные хранилища данных, называемые таблицами символов, или таблицами идентификаторов.
Любая таблица идентификаторов состоит из набора полей, количество которых равно числу различных идентификаторов, найденных в исходной программе. Каждое поле содержит в себе полную информацию о данном элементе таблицы. Компилятор может работать как с одной, так и с несколькими таблицам идентификаторов.
Состав информации, хранимой в таблице идентификаторов для каждого элемента исходной программы, зависит от семантики входного языка и типа элемента. Так для переменных могут храниться: имя переменной, тип данных и область памяти, связанная с переменной; для функций – имя функции, количество и типы формальных аргументов функции, тип возвращаемого результата; адрес кода функции.
Не вся информация, хранимая в таблице идентификаторов, заполняется компилятором одновременно. Имена переменных могут быть выделены на фазе лексического анализа, типы данных для них – на фазе синтаксического разбора, а область памяти – на фазе подготовки к генерации кода. Таким образом, на разных фазах компиляции компилятор многократно обращается к таблице для поиска информации и записи новых данных.
Таблицы идентификаторов организуются таким образом, чтобы компилятор имел возможность максимально быстрого поиска требуемого ему элемента.
Простейший способ ее организации состоит в добавлении новых элементов в порядке их поступления. В этом случае таблица идентификаторов представляет собой неупорядоченный массив информации. Поиск нужного элемента заключается в последовательном сравнении искомого элемента с каждым элементом таблицы. Тогда для поиска в таблице, содержащей n элементов, в среднем будет выполнено n/2 сравнений. Такой способ организации таблиц идентификаторов является неэффективным.
|
|
|
Поиск более эффективен в таблице, элементы которой упорядочены (отсортированы) согласно некоторому порядку. Методом поиска в упорядоченном списке является бинарный (или логарифмический) поиск.
Его алгоритм состоит в следующем: искомый символ сравнивается с элементом в середине таблицы (с порядковым номером (N + 1)/2). Если этот элемент не является искомым, то просматривается только блок элементов, пронумерованных от 1 до (N + 1)/2 – 1, или блок элементов от (N + 1)/2 + 1 до N в зависимости от того, меньше или больше искомый элемент по сравнению с ранее найденным. Так продолжается до тех пор, пока либо искомый элемент не будет найден, либо алгоритм дойдет до очередного блока, содержащего один или два элемента, с которыми можно выполнить прямое сравнение искомого элемента.
Так как на каждом шаге число элементов, которые могут содержать искомый элемент, сокращается в 2 раза, максимальное число сравнений равно 1+log2(N).
Недостатком данного метода является требование упорядочивания элементов таблицы идентификаторов. Время упорядочивания напрямую зависит от числа элементов в массиве. Таблица идентификаторов зачастую просматривается компилятором еще до того, как она заполнена полностью, поэтому для построения такой таблицы можно пользоваться только алгоритмом прямого упорядоченного включения элементов.
Для сокращения времени поиска искомого элемента в таблице идентификаторов без значительного увеличения времени ее заполнения, надо отказаться от организации таблицы в виде непрерывного массива данных.
|
|
|
Например, существует метод построения таблиц в форме бинарного дерева. Каждый узел такого дерева представляет собой элемент таблицы, причем корневой узел является первым элементом, встреченным при заполнении таблицы. Дерево называется бинарным, так как каждая вершина в нем может иметь не более двух ветвей. Для определенности их называют «правая» и «левая».
Первый идентификатор помещается в вершину дерева. Все дальнейшие идентификаторы попадают в дерево по следующему алгоритму:
Шаг 1. Выбрать очередной идентификатор из входного потока данных. Если его нет – построение дерева закончено.
Шаг 2. Сделать текущим узлом дерева корневую вершину.
Шаг 3. Сравнить очередной идентификатор с идентификатором, содержащимся в текущем узле дерева.
Шаг 4. Если очередной идентификатор меньше, то перейти к шагу 5, если равен – сообщить об ошибке и прекратить выполнение алгоритма (двух одинаковых идентификаторов быть не должно!), иначе перейти к шагу 7.
Шаг 5. Если у текущего узла существует левая вершина, сделать ее текущим узлом и вернуться к шагу 3, иначе перейти к шагу 6.
Шаг 6. Создать новую вершину, поместить в нее очередной идентификатор, сделать эту новую вершину левой вершиной текущего узла и вернуться к шагу 1.
Шаг 7. Если у текущего узла существует правая вершина, сделать ее текущим узлом и вернуться к шагу 3, иначе перейти к шагу 8.
Шаг 8. Создать новую вершину, поместить в нее очередной идентификатор, сделать эту новую вершину правой вершиной текущего узла и вернуться к шагу 1.
Поиск нужного элемента в дереве выполняется по алгоритму, схожему с алгоритмом заполнения дерева:
Шаг 1. Сделать текущим узлом дерева корневую вершину.
Шаг 2. Сравнить искомый идентификатор с идентификатором, содержащимся в текущем узле дерева.
Шаг 3. Если идентификаторы совпадают, искомый идентификатор найден, алгоритм завершен, иначе надо перейти к шагу 4.
Шаг 4. Если очередной идентификатор меньше, перейти к шагу 5, иначе перейти к шагу 6.
Шаг 5. Если у текущего узла существует левая вершина, сделать ее текущим узлом и вернуться к шагу 2, иначе искомый идентификатор не найден, алгоритм завершен.
Шаг 6. Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 2, иначе искомый идентификатор не найден, алгоритм завершен.
|
|
|
Для данного метода число требуемых сравнений и форма дерева зависят от порядка, в котором поступают идентификаторы. Недостатком метода является необходимость работы с динамическим выделением памяти при построении дерева.
В целом метод бинарного дерева является довольно удачным механизмом для организации таблиц идентификаторов. Он нашел свое применение в ряде компиляторов. Иногда компиляторы строят несколько различных деревьев для идентификаторов разных типов и разной длины.
Лучших результатов можно достичь, если применить методы, связанные с использованием хэш-функций и хэш-адресации.
Хэш-функцией F называется некоторое отображение множества входных элементов R на множество целых неотрицательных чисел Z: F(r) = n, r  R, n
R, n  Z. Множество допустимых входных элементов R называется областью определения хэш-функции. Множеством значений хэш-функции F называется подмножество М из множества целых неотрицательных чисел Z: M
Z. Множество допустимых входных элементов R называется областью определения хэш-функции. Множеством значений хэш-функции F называется подмножество М из множества целых неотрицательных чисел Z: M  Z, содержащее все возможные значения, возвращаемые функцией F:
Z, содержащее все возможные значения, возвращаемые функцией F:  r
r  R: F(r)
R: F(r)  M и
M и  m
m  M:
M: 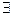 r
r  R: F(r) = m. Процесс отображения области определения хэш-функции на множество значений называется «хэшированием».
R: F(r) = m. Процесс отображения области определения хэш-функции на множество значений называется «хэшированием».
При работе с таблицей идентификаторов хэш-функция выполняет отображение имен идентификаторов на множество целых неотрицательных чисел. Областью определения такой хэш-функции будет множество всех возможных имен идентификаторов.
Хэш-адресация заключается в использовании значения, возвращаемого хэш-функцией, в качестве адреса ячейки из некоторого массива данных. Тогда размер массива данных должен соответствовать области значений используемой хэш-функции. Следовательно, в реальном компиляторе область значений хэш-функции не должна превышать размер доступного адресного пространства компьютера.
Метод организации таблиц идентификаторов, основанный на использовании хэш-адресации, заключается в размещении каждого элемента таблицы в ячейке, адрес которой возвращает хэш-функция, вычисленная для этого элемента. Для помещения каждого элемента в таблицу идентификаторов требуется вычисление его хэш-функции и размещения его по вычисленному адресу. Первоначально таблица идентификаторов должна содержать пустые ячейки.
|
|
|
Для поиска требуемого элемента в таблице также вычисляется хэш-функция и проверяется содержимое соответствующей ячейки. Если она не пуста – элемент найден, иначе – не найден.
Время размещения элемента в таблице и время его поиска определяются только временем, затрачиваемым на вычисление хэш-функции, которое в общем случае несопоставимо меньше времени, необходимого для выполнения многократных сравнений элементов таблицы. Но метод имеет два очевидных недостатка. Первый из них неэффективное использование объема памяти под таблицу идентификаторов: размер массива для ее хранения должен соответствовать области значений хэш-функции, в то время как реально хранимых в таблице идентификаторов может быть существенно меньше. Второй – необходимость соответствующего разумного выбора хэш-функции.
Если двум или более идентификаторам соответствует одно и то же значение функции, такая ситуация называется коллизией. Хэш-функция, допускающая хотя бы единичную коллизию, не может быть напрямую использована для хэш-адресации в таблице идентификаторов.
Для полного исключения коллизий хэш-функция должна быть взаимно однозначной, т.е. каждому элементу из области определения хэш-функции должно соответствовать только одно значение из ее множества значений, и каждому значению из множества значений этой функции должен соответствовать только один элемент из области ее определения.
В реальности область значений любой хэш-функции ограничена размером доступного адресного пространства в данной архитектуре компьютера. Множество адресов любого компьютера с традиционной архитектурой может быть велико, но всегда конечно. Организовать взаимно однозначное отображение бесконечного множества имен идентификаторов на конечное множество невозможно.
Существует несколько способов для разрешения проблемы коллизии. Одним из них является метод рехэширования (расстановки). В нем, если для элемента А адрес h(A), вычисленный с помощью хэш-функции h, указывает на уже занятую ячейку, то необходимо вычислить новое значение n1 = h1(A) и проверить занятость ячейки по адресу n1. Если и она занята, то вычисляется значение h2(А) и так до тех пор, пока либо не будет найдена свободная ячейка, либо очередное значение hi(A) совпадет с h(A). В последнем случае считается, что таблица идентификаторов заполнена, и места в ней больше нет.
|
|
|
Тогда таблицу идентификаторов можно организовать по следующему алгоритму размещения элемента:
Шаг 1. Вычислить значение хэш-функции n = h(A) для нового элемента А.
Шаг 2. Если ячейка по адресу n пустая, поместить в нее элемент А и завершить алгоритм, иначе i = 1 и перейти к шагу 3.
Шаг 3. Вычислить ni= hi (A). Если ячейка по адресу ni пустая, то поместить в нее элемент А и завершить алгоритм, иначе перейти к шагу 4.
Шаг 4. Если n = niто сообщить об ошибке и завершить алгоритм, иначе i = i+1 и вернуться к шагу 3.
Поиск элемента А в таблице идентификаторов, организованной таким образом, будет выполняться по следующему алгоритму:
Шаг 1. Вычислить значение хэш-функции n= h(A) для искомого элемента А.
Шаг 2. Если ячейка по адресу n пуста, то элемент не найден, алгоритм завершен. Иначе сравнить имя элемента в ячейке n с именем искомого элемента А. Если они совпадают – элемент найден и алгоритм завершен, иначе i = 1, перейти к шагу 3.
Шаг 3. Вычислить ni = hi(A). Если ячейка по адресу ni пустая или n = niто элемент не найден и алгоритм завершен, иначе сравнить имя элемента в ячейке ni с именем искомого элемента А. Если они совпадают, то элемент найден и алгоритм завершен, иначе i = i + 1 и повторить шаг 3.
Алгоритмы размещения и поиска элемента схожи по выполняемым операциям и имеют одинаковые оценки времени, необходимого для их выполнения.
При такой организации таблиц идентификаторов при возникновении коллизии алгоритм пытается поместить элемент в пустую ячейку, что может привести к возникновению новой, дополнительной коллизии. Поэтому количество операций, необходимых для поиска или размещения в таблице элемента, зависит от степени заполнения таблицы.
Важно определить хэш-функцию hi для каждого i. Чаще всего функции hi определяют как некоторые модификации первоначальной хэш-функции h. Например, самым простым методом вычисления функции hi(A) является ее организация в виде hi(A) = (h(A) + рi)mod Nm, где рi – некоторое вычисляемое целое число, a Nm – максимальное значение из области значений хэш-функции h. Простейшим случаем будет задать рi = i. Тогда при совпадении значений хэш-функции для каких-либо элементов поиск свободной ячейки в таблице начинается последовательно от текущей позиции, заданной значением хэш-функции h(A). В этом случае при совпадении хэш-адресов элементы в таблице начинают группироваться вокруг них, что увеличивает число необходимых сравнений при их поиске и размещении.
Но даже такой примитивный метод рехэширования является достаточно эффективным средством организации таблиц идентификаторов при частном заполнении таблицы. Имея, например, заполненную на 90% таблицу для 1024 идентификаторов, в среднем необходимо выполнить 5.5 сравнений для поиска одного идентификатора, в то время как даже логарифмический поиск дает в среднем от 9 до 10 сравнений.
Лучшие результаты дает использование в качестве рi последовательности псевдослучайных целых чисел p1, p2,..., pk или при вычислении по формуле hi(A) = (h(A)*i) mod Nm, если Nm – простое число. В целом, рехэширование позволяет добиться неплохих результатов, но требование частичного заполнения таблицы ведет к неэффективному использованию объема доступной памяти.
Частичное заполнение таблицы идентификаторов при применении хэш-функций ведет к неэффективному использованию всего объема памяти, доступного компилятору. Этого недостатка можно избежать, дополнив таблицу идентификаторов специальной промежуточной хэш-таблицей. В ее ячейках может храниться либо пустое значение, либо значение указателя на некоторую область памяти из основной таблицы идентификаторов. Тогда после вычисления значения хэш-функции определяется адрес, по которому происходит обращение сначала к промежуточной хэш-таблице, а через нее – к самой таблице идентификаторов. Тогда иметь в самой таблице идентификаторов ячейку для каждого возможного значения хэш-функции не обязательно и таблицу можно сделать динамической. Количество ячеек в ней будет равно числу идентификаторов. Пустые ячейки будут только в хэш-таблице. Способ реализации такой схемы называется «метод цепочек». Он работает по следующему алгоритму:
Шаг 1. Во все ячейки хэш-таблицы поместить пустое значение, таблица идентификаторов пуста, переменная FreePtr (указатель первой свободной ячейки) указывает на начало таблицы идентификаторов; i = 1.
Шаг 2. Вычислить значение хэш-функции niдля нового элемента Аi. Если ячейка хэш-таблицы по адресу niпустая, поместить в нее значение переменной FreePtr и перейти к шагу 5; иначе перейти к шагу 3.
Шаг 3. Положить j=1, выбрать из хэш-таблицы адрес ячейки таблицы идентификаторов mj и перейти к шагу 4.
Шаг 4. Для ячейки таблицы идентификаторов по адресу mj проверить значение поля ссылки. Если оно пустое, записать в него адрес из переменной FreePtr и перейти к шагу 5; иначе j = j + 1, выбрать из поля ссылки адрес mj и повторить шаг 4.
Шаг 5. Добавить в таблицу идентификаторов новую ячейку, записать в нее информацию для элемента Аi (поле ссылки должно быть пустым), в переменную FreePtr поместить адрес, следующий за добавленной ячейкой. Если больше нет идентификаторов для размещения в таблице, алгоритм завершен, иначе i = i + 1 и перейти к шагу 2.
Поиск элемента в таблице идентификаторов, организованной таким образом, будет выполняться по следующему алгоритму:
Шаг 1. Вычислить значение хэш-функции n для искомого элемента А. Если ячейка хэш-таблицы по адресу n пустая, то элемент не найден и алгоритм завершен, иначе j = 1, выбрать из хэш-таблицы адрес ячейки таблицы идентификаторов mj.
Шаг 2. Сравнить имя элемента в ячейке таблицы идентификаторов по адресу mj с именем искомого элемента А. Если они совпадают, искомый элемент найден и алгоритм завершен, иначе перейти к шагу 3.
Шаг 3. Проверить значение поля ссылки в ячейке таблицы идентификаторов по адресу mj. Если оно пустое, то искомый элемент не найден и алгоритм завершен; иначе j = j + 1, выбрать из поля ссылки адрес mj и перейти к шагу 2.
В случае возникновения коллизии алгоритм размещает элементы в ячейках таблицы, связывая их друг с другом последовательно через поле ссылки. При этом элементы не могут попадать в ячейки с адресами, которые потом будут совпадать со значениями хэш-функции. Таким образом, дополнительные коллизии не возникают. В итоге в таблице возникают своеобразные цепочки связанных элементов, откуда происходит и название данного метода.
В реальных компиляторах практически всегда, так или иначе, используется хэш-адресация. Часто применяются комбинированные методы. В этом случае, как и для метода цепочек, в таблице идентификаторов организуется специальное дополнительное поле ссылки. Но в отличие от метода цепочек оно имеет несколько иное значение. При отсутствии коллизий для выборки информации из таблицы используется хэш-функция, поле ссылки остается пустым. Если же возникает коллизия, го с помощью поля ссылки организуется поиск идентификаторов, для которых значения хэш-функции совпадают, по одному из рассмотренных выше методов: неупорядоченный список, упорядоченный список или же бинарное дерево. При хорошо построенной хэш-функции коллизии будут возникать редко.
Хэш-адресация – метод, который применяется не только для организации таблиц идентификаторов в компиляторах, но и нашел свое применение в операционных системах, и в системах управления базами данных.
Контрольные вопросы
1. Какая информация хранится в таблице идентификаторов?
2. Какие способы организации таблиц идентификаторов существуют?
3. Когда и по какой причине возникает коллизия при организации таблиц идентификаторов с использованием хэш-функции?
4. Каковы требования к списку идентификаторов при использовании метода логарифмического поиска в таблице идентификаторов?
5. В чем заключается преимущество метода цепочек по сравнению с методом рехэширования?
6. Выберите неверное утверждение:
а) область значений любой хэш-функции ограничена размером доступного адресного пространства в данной архитектуре компьютера;
б) вся информация, хранимая в таблице идентификаторов, заполняется компилятором одновременно;
в) для полного исключения коллизий хэш-функция должна быть взаимно однозначной;
г) состав информации, хранимой в таблице идентификаторов для каждого элемента исходной программы, зависит от семантики входного языка и типа элемента.
7. Использование значения, возвращаемого хэш-функцией, в качестве адреса ячейки из некоторого массива данных называется
а) хэш-адресацией б) хэш-функцией
в) хэшированием г) рехэшированием
Задание
1. а) Написать программу, реализующую создание таблицы идентификаторов по методу логарифмического поиска. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать коды первых двух букв идентификаторов;
в)Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
2. а) Написать программу, реализующую метод бинарного дерева для построения таблицы идентификаторов. Для организации дерева использовать динамический массив. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать коды первых двух букв идентификаторов;
в)Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
3. а) Написать программу, реализующую создание таблицы идентификаторов по методу логарифмического поиска. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать коды последних двух букв идентификаторов;
в)Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
4. а) Написать программу, реализующую метод бинарного дерева для построения таблицы идентификаторов. Для организации дерева использовать динамический массив. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать коды последних двух букв идентификаторов;
в)Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
5. а) Написать программу, реализующую создание таблицы идентификаторов по методу логарифмического поиска. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать некоторое случайное число в диапазоне от -10 до 10;
в) Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
6. а) Написать программу, реализующую метод бинарного дерева для построения таблицы идентификаторов. Для организации дерева использовать динамический массив. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать некоторое случайное число в диапазоне от -10 до 10;
в) Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
7. а) Написать программу, реализующую создание таблицы идентификаторов по методу логарифмического поиска. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать номер текущего вычисления хэш-функции;
в) Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
8. а) Написать программу, реализующую метод бинарного дерева для построения таблицы идентификаторов. Для организации дерева использовать динамический массив. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать номер текущего вычисления хэш-функции;
в) Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
9. а) Написать программу, реализующую создание таблицы идентификаторов по методу логарифмического поиска. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать сумму кодов символов идентификатора;
в) Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
10. а) Написать программу, реализующую метод бинарного дерева для построения таблицы идентификаторов. Для организации дерева использовать динамический массив. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами.
б) Написать программу, реализующую создание таблицы идентификаторов на основе метода рехэширования. В качестве исходных данных использовать файл, считая в нем все исходные слова идентификаторами. В качестве хэш-функции использовать сумму кодов символов идентификатора;
в) Написать программу, реализующую создание таблицы идентификаторов методом цепочек с хэш-функцией из предыдущего задания.
г) Сравнить реализованные методы построения таблиц идентификаторов.
|
|
|


