 |
Краткие теоретические сведения.
|
|
|
|
Деление окружности на равные части
Некоторые детали имеют элементы, равномерно распределенные по окружности. При выполнении чертежей деталей, имеющих подобные элементы, необходимо уметь делить окружность на равные части. Приемы деления окружности на равные части приведены на рис. 3.1.
Рис. 3.1 - Деление окружности на равные части
С достаточной точностью можно делить окружность, на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины ходы.
По количеству равных отрезков на окружности (таблица 3) находим соответствующий коэффициент. При перемножении полученного коэффициента на диаметр окружности, получаем длину хорды, которую циркулем откладываем на окружности.
Таблица 3
Коэффициент для определения длинны хорды
| Количество частей окружности | Коэффициент |
| 0,866025 0,707107 0,587785 0,433884 0,382633 0,342620 0,309017 0,281733 0,258810 0,239316 0,222521 0,207912 0,105090 0,183750 0,173648 0,164595 |
Выполнение сопряжения между двумя линиями
При вычерчивании контуров технических деталей и в других технических построениях часто приходится выполнять сопряжения (плавные переходы) от одних линий к другим. Сопряжение двух сторон угла дугой заданного радиусу дуги R выполняют в следующей последовательности:
- параллельно сторонам угла на расстоянии, равном R, проводят две вспомогательные прямые линии;
- точка пересечения этих прямых будет центром сопряжения;
- из центра сопряжения выполняют перпендикуляры на заданные прямые;
- точки пересечения перпендикуляров с заданными прямыми называют точками сопряжения;
- из центра сопряжения строят дугу радиусом R, соединяя точки сопряжения.
На рис. 3.2 приведены примеры построения сопряжений, когда задан радиус дуги сопряжения. В этом случае необходимо определить центр сопряжения и точки сопряжения. Обводку контура детали производят с помощью циркуля.
|
|
|
Рис. 3.2 - Приемы построения сопряжений
Построение лекальных кривых
В технике часто приходится вычерчивать кривые линии, составленные из большого количества малых дуг окружностей с постепенным изменением радиуса их кривизны. Такие линии невозможно провести циркулем. Эти кривые вычерчивают с помощью лекал и называют лекальными. Необходимо изучить закономерность образования лекальной кривой и нанести на чертёж ряд принадлежащих ей точек. Точки соединяют плавной кривой тонкой линией от руки, а обводку выполняют с помощью лекала.
Для обводки лекальных кривых нужно иметь набор нескольких лекал. Выбрав подходящее лекало, подгоняют кромку части лекала к возможно большему количеству найденных точек. Чтобы обвести следующий участок, нужно подогнать кромку лекала ещё к двум-трём точкам, при этом лекало должно касаться части уже обведённой кривой. Способ проведения кривой по лекалу приведён на рис. 3.3.
Рис. 3.3 - Построение кривой по лекалу.
На рис. 3.4 показан пример построения эллипса по заданным осям AB и CD.
Рис. 3.4 - Построение эллипса
На рис. 3.5 показан пример построения параболы с помощью деления сторон угла AOC на одинаковое количество равных частей. На рис. 3.6 дан пример построения эвольвенты окружности. Заданная окружность разделена на 12 равных частей. Через точки деления проведены касательные к окружности. На касательной, проведённой через точку 12, отложена длина данной окружности и разделена на 12 равных частей. Начиная от точки l на касательных к окружности, последовательно откладывают отрезки, равные 1/12 длины окружности, 1/6, 1/4 и т. д.
Рис. 3.5 - Построение параболы
Рис. 3.6 - Построение эвольвенты
|
|
|
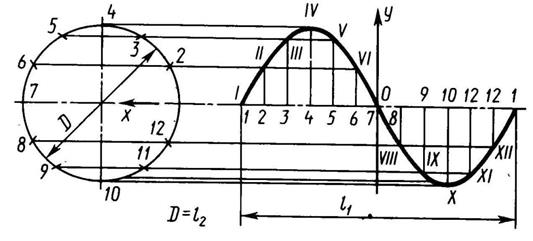
Рис. 3.7 - Построение синусоиды
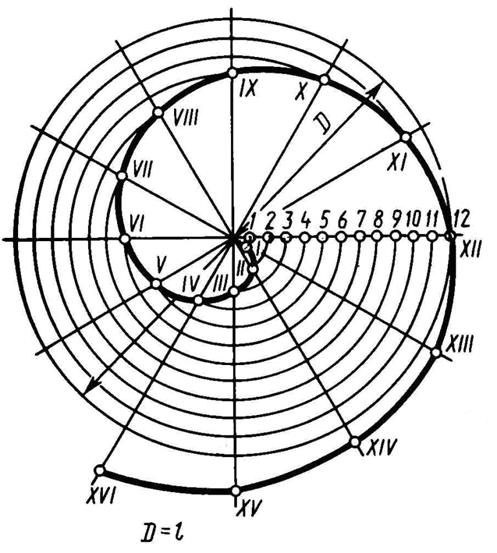
Рис.3.8 - Построение спирали Архимеда
На рис. 3.7 показан приём построения синусоиды. Заданная окружность разделена на 12 равных частей, на такое же число равных частей делится отрезок прямой, равный длине развёрнутой окружности (l1). Проведя через точки деления горизонтальные и вертикальные прямые, находят в их пересечении точки синусоиды.
На рис. 3.8 показан пример построения спирали Архимеда. Для построения её делят заданную окружность на 12 равных частей, радиус окружности также делим на 12 равных частей. Проводят лучи из центра через точки деления окружности. Откладывают на первом луче одно деление радиуса, на втором – два и т. д., получают ряд точек спирали, которые соединяют с помощью лекала.
Нанесение размеров
Для нанесения размеров по ГОСТ 2.307-68 применяются размерные и выносные линии (тонкие, сплошные), а также размерные числа.
Размерные и выносные линии
Размерные линии проводят параллельно измеряемому отрезку или по концентрической дуге измеряемого угла и ограничиваются стрелками. Общие правила нанесения размерных и выносных линий показаны на рис.3.9.
Рис. 3.9 - Стрелки и выносные линии
Размерные линии предпочтительно наносить вне контура изображения.
Допускается проводить линии непосредственно к линиям видимого контура, осевым, центровым и другим линиям.
Необходимо избегать пересечения размерных и выносных линий.
Не допускается использовать линии контура, осевые, центровые и выносные линии в качестве размерных линий.
При недостатке места для стрелок на размерных линиях, расположенных цепочкой, стрелки допускается заменять засечками, наносимыми под углом 45° к размерным линиям, или четко наносимыми точками (рис 3.10).
Рис.3.10 - Нанесение размеров по цепочке
Размерные числа
Линейные размеры на чертежах указывают в мм, а угловые – в градусах и минутах с обозначение единицы измерения.
Размерное число высотой 5 мм наносят над размерной линией на расстоянии 0,5..1 мм как можно ближе к середине (рис. 3.11). Над параллельными прямыми (или концентрическими дугами) размерные числа располагаются в шахматном порядке.
Рис. 3.11 - Нанесение линейных и угловых размеров
|
|
|
Размерные числа линейных размеров при различных наклонах размерных линий располагаются, как показано на рис. 3.12.
Рис. 3.12 - Нанесение наклонных размеров
Если необходимо нанести размер в заштрихованной зоне, то размерное число располагается на полке линии-выноски (рис. 3.13).
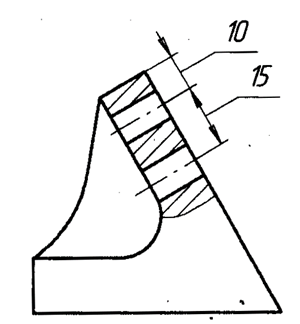
Рис. 3.13 - Нанесение размера в заштрихованной зоне
Простановка угловых размеров показана на рис. 3.14, в заштрихованной зоне угловые размерные числа наносятся на полке линии-выноски.
Рис. 3.14 - Нанесение угловых размеров
Нанесение размеров диаметра или радиусов
При указании диаметра применяется знак, который наносится перед размерным числом (рис. 3.15).
Рис. 3.15 - Обозначение диаметра
Некоторые из вариантов простановки диаметральных размеров показаны на рис. 3.16.
Рис. 3.16 - Нанесение значений диаметра
При нанесении размера радиуса перед размерным числом помещается приписная латинская R (рис.3.18). Варианты простановки размеров радиуса также показаны на рис.3.17.
Рис.3.17 - Простановка размеров радиуса
При большой величине радиуса центр допускается приближать к дуге, в этом случае размерная линия радиуса показывается с изломом под углом 90°. Если не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается не доводить до центра и смещать ее относительно центра. Если радиусы скруглений, сгибов и т.д. на всем чертеже одинаковы или какой-либо радиус является преобладающим, то вместо нанесения размеров этих радиусов непосредственно на изображении рекомендуется в технических требованиях делать запись типа: «Неуказанные радиусы 8 мм», «Радиусы скруглений 4 мм» и т.д.
Размеры нескольких одинаковых элементов изделия, как правило, наносятся один раз с указанием на полке линии-выноски количества этих элементов. Размеры небольших конических и пирамидальных срезов (фасок) на деталях проставляются, как показано на рис. 3.18.
Рис. 3.18 - Особые случаи простановки размеров
Задание
|
|
|
Вычертить контур железнодорожной детали, представленной в ПРИЛОЖЕНИИ А и нанести размеры.
Ход работы
1. Выбрать вариант задания. Вариант задания определяется номером студента по списку в журнале.
2. На формате А3 чертежной бумаги выбрать рабочую сторону (более гладкая на ощупь).
3. Расположить формат горизонтально и определить рабочую область, вычертив рамку по заданным ГОСТом размерам.
4. Мысленно разделить рабочую область пополам. В левой части листа выполняют деталь с элементами, расположенными по окружности. В правой части листа выполняют деталь с разрезом и штриховкой.
5. Нанести на чертежи деталей заданные размеры чертежным шрифтом 5 размера.
6. Обвести мягким карандашом контуры деталей, основную надпись, рамку. Стереть вспомогательные линии построения.
Образец выполненной работы представлен на рис.3.19.
Контрольные вопросы
1. Какими способами можно разделить окружность на три равные части?
2. Как разделить окружность на любое равное количество частей, зная, что окружность составляет 360°?
3. Что называется сопряжением? Какие виды сопряжений Вам известны?
4. Как построить внутреннее сопряжение двух окружностей?
5. Какие лекальные кривые Вам известны?
6. Каковы правила простановки размеров на чертежах?
Рис. 3.19 - Образец выполнения практической работы
Практическая работа №4
|
|
|
