 |
Правила вычисления первообразной функции
|
|
|
|
Определение: Функция F(x) называется первообразной для функции f(x), если  .
.
| Функция | Первообразная |
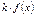
| 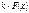
|

| 
|
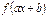
| 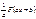
|
Правила вычисления производной функции

| 
|
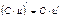
| |

|  Сложная функция: Сложная функция:

|

|
Производные элементарных функций
| № | Функция | Производная | № | Функция | Производная | ||
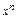
| 
| 
| 
| ||||

| 
| 
| 
| ||||

| 
| ||||||

| 
| ||||||

| 
| ||||||

| 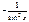
| 
| 
|
Равносильные уравнения:
| Исходное уравнение | Равносильное уравнение (система) | |

| Û | 
|
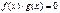
| Û | 
|
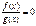
| Û | 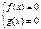
|
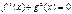
| Û | 
|
Числовые множества:
| Натуральные числа | N = { 1; 2; 3; 4;..} |
| Целые числа | Z = N È { 0; -1; -2; -3; …} |
| Рациональные числа | Q = Z È 
|
| Действительные числа | R = Q È 
|
Тригонометрия
Основные триг. формулы
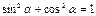 Þ
Þ 
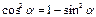
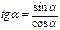
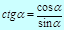 Þ
Þ 


Формулы суммы функций


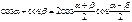

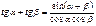

Формулы суммы аргументов:
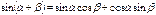

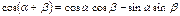
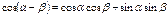


Формулы произведения функций



Формулы половинного аргумента



Формулы двойного аргумента
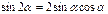


Формула дополнительного угла
 где
где


 Определение тригонометрических функций
Определение тригонометрических функций
Универсальная подстановка
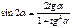
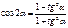
Свойства тригонометрических функций
| Функция | Свойства | |||
| Область определения | Множество значений | Четность-нечетность | Период | |
| cosx | 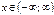
| 
| cos(-x)= cosx | 2p |
| sinx | 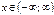
| 
| sin(-x)= -sinx | 2p |
| tgx | 
| 
| tg(-x)= -tgx | p |
| ctgx | 
| 
| ctg(-x)= -ctgx | p |
Тригонометрические уравнения
Косинус:




Уравнения с синусом
Частные формулы:



Общая формула:
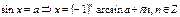
Уравнения с тангенсом и котангенсом
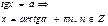

Формулы обратных триг функций


| Если 0 < x £ 1, то arccos(-x) = p - arccosx arcsin(-x) = - arcsinx | Если x > 0, то arctg(-x) = - arctgx arcctg(-x) = p - arcctgx |
Обратные триг функции
| Функция | Свойства | ||
| Область определения | Множество значений | ||
| arccosx | 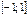
| [ 0; p ] | |
| arcsinx | 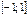
| [-p/2; p/2] | |
| arctgx | 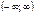
| (-p/2; p/2) | |
| arcctgx | 
| (0; p) | |
Геометрия
|
|
|
 Теорема косинусов, синусов
Теорема косинусов, синусов
Теорема косинусов:

Теорема синусов:

Площадь треугольника

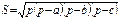
 | 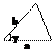 | ||||
 |


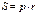
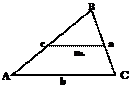 Средняя линия
Средняя линия
Средняя линия – отрезок, с соединяющий середины двух с сторон треугольника.
Средняя линия параллельна т третьей стороне и равна е её половине: 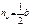
Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного
Равносторонний треугольник
треугольник, у которого все стороны равны.
v Все углы равны 600.
v Каждая из высот является одновременно биссектрисой и медианой.
v Центры описанной и вписанной окружностей совпадают.
v Радиусы окружностей: 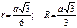
Площадь 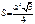
Равнобедренный треугольник
треугольник, у которого две стороны равны.
 1.Углы, при основании треугольника, равны
1.Углы, при основании треугольника, равны
2.Высота, проведенная из вершины, является б биссектрисой и медиан
|
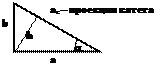 |
v Теорема Пифагора:  Площадь:
Площадь: 
v Тригонометрические соотношения: 
v Центр описанной окружности лежит на середине гипотенузы.
v Радиусы окружностей: 
v Высота, опущенная на гипотенузу: 
v Катеты: 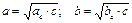
Основные соотношения в треугольнике
Ø Неравенство треугольника:
a + b > c; a + c > b; b + c > a
Ø Сумма углов: a + b + g = 1800
Ø Против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
Ø 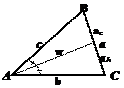 Против равных сторон лежат равные углы, и обратно, против равных углов лежат равные стороны.
Против равных сторон лежат равные углы, и обратно, против равных углов лежат равные стороны.
Биссектриса
|
|
|
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
· Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам: ab: ac = b: c
· Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
· 

 Конус
Конус

|
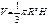


|
 |
Усеченный конус
 |


 |
 Вписанная окружность
Вписанная окружность
· Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
· Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой:
a + b = c + d
Описанная окружность
Касательная, секущая 

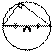
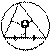
·
· Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
· Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
· Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
· Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой: 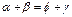
Длина окружности, площадь
 |


 |

 Хорда
Хорда
Хорда – отрезок, соединяющий две точки окружности.
· Диаметр, делящий хорду пополам, перпендикулярен хорде.
· В окружности равные хорды равноудалены от центра окружности.
· Отрезки пересекающихся хорд связаны равенством:

Шар
 |


 |
Шаровой сектор



Шаровой сегмент

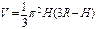
|
|
|


